
- •I. Четырехполюсники.
- •1. Основные определения и классификация четырехполюсников.
- •2. Системы уравнений четырехполюсников.
- •3. Входное сопротивление четырехполюсника при произвольной нагрузке.
- •4. Соединения четырехполюсника.
- •II. Переходные процессы в электрических цепях.
- •6. Переходные процессы в rLc цепи(последовательном контуре).
- •7. Общий случай расчета переходных процессов классическим методом.
- •8. Основные положения операторного метода расчета переходных процессов в электрических цепях.
- •9. Изображение напряжения на индуктивности.
- •11. Закон Ома в операторной форме. Внутренние эдс.
- •12. Первый закон Кирхгофа в операторной форме
- •13. Второй закон Кирхгофа в операторной форме
- •12. Первый закон Кирхгофа в операторной форме.
- •14. Расчет переходных процессов операторным методом в rc контуре при ступенчатом воздействии.
- •13. Второй закон Кирхгофа в операторной форме.
- •15. Расчет переходных процессов операторным методом в параллельном колебательном контуре при ступенчатом воздействии.
- •16. Расчет переходных процессов операторным методом в параллельном колебательном контуре при гармоническом воздействии
- •17. Последовательность расчета пп операторным методом
- •18. Расчет переходных процессов методом переменных состояния.
- •19. Последовательность расчета переходных процессов методом переменных состояния.
- •20. Численный метод решения уравнений состояния динамической цепи.
- •III. Периодические несинусоидальные токи в электрических цепях.
- •1. Основные понятия о несинусоидальных эдс, напряжениях, тока и методах анализа.
- •2. Действующие и средние значения несинусоидальных электрических величин.
- •4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.
- •3. Активная мощность при несинусоидальных напряжении и токе.
- •4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.
- •5. Несинусоидальные кривые с периодической огибающей. Биения
- •7. Высшие гармоники в трехфазных цепях.
- •IV. Цепи (линии) с распределенными параметрами.
- •1. Направляющие сис-мы передачи электроэнергии и их модели.
- •2. Уравнение двухпроводной линии
- •3.Уравнения многопроводных линий
- •4.Расчет процессов в цепях с распределенными параметрами.
- •5.Установившиеся режимы в линиях.
- •V. Нелинейные электрические цепи.
- •1. Нелинейные элементы и их вольтамперные характеристики.
- •2. Последовательное соединение нелинейных элементов.
- •3. Параллельное соединение нелинейных элементов.
- •4. Смешанное соединение нелинейных элементов.
- •5. Статические и дифференциальный сопротивления.
- •6. Замена нелинейного элемента линейным сопротивлением и эдс.
- •VI. Магнитные цепи.
- •2. Закон Ома и законы Кирхгофа для магнитных цепей.
- •3.Расчет неразветвленных магнитных цепей.
- •4. Расчет разветвленных магнитных цепей.
- •5. Магнитные цепи переменного тока.
- •VII. Теория электромагнитного поля.
- •1. Электромагнитное поле и его уравнение в интегральной форме.
- •2. Закон полного тока в дифференциальной форме (первое уравнение максвелла )
- •3. Закон электромагнитной индукции в дифференциальной форме(второе уравнение максвелла)
- •4. Теорема гаусса и постулат максвелла в дифференциальной форме
- •5. Выражение в дифференциальной форме принципов непрерывности магнитного потока и непрерывности электрического тока.
- •8. Уравнение Пуассона и Лапласа для электростатического поля
- •9. Уравнение Максвелла в комплексном виде. Волновое уравнение Гельмгольца
- •11. Вектор Пойнтинга
- •12. Вывод волновых уравнений непосредственно из уравнений Максвелла в дифференциальной форме
- •10. Основные свойства плоских электромагнитных волн
- •13. Численные методы расчета электромагнитных полей. Граничные условия
12. Первый закон Кирхгофа в операторной форме
Алгебраическая
сумма операторных токов в узле равна
нулю.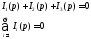
13. Второй закон Кирхгофа в операторной форме
Для любого замкнутого контура любой электрической цепи можно составить уравнение по второму закону Кирхгофа для мгновенных значений. Предварительно необходимо выбрать положительные направления для токов в ветвях и направление обхода контура.
Запишем уравнение
по второму закону Кирхгофа для контура
рис. 8.28. Контур обходим по часовой
стрелке. Учтем, что индуктивности
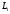 и
и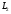 связаны магнитно. При выбранных
положительных направлениях для токов
связаны магнитно. При выбранных
положительных направлениях для токов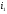 и
и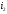 между
между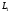 и
и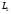 имеет место согласное включение.
имеет место согласное включение.
Падение напряжения
на
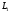 равно
равно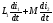 ;—
на
;—
на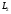 составляет
составляет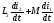 . При составлении уравнения учтем, что
начальное напряжение на конденсаторе
равно
. При составлении уравнения учтем, что
начальное напряжение на конденсаторе
равно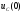 .
Пусть оно действует согласно с током
.
Пусть оно действует согласно с током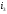 .
Начальное значение
.
Начальное значение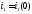 тока
тока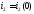 Имеем
Имеем
 (8.44)
(8.44)
Каждое из слагаемых (8.44) заменим операторным изображением:
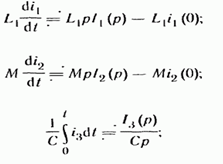
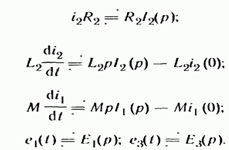 (8.45)
(8.45)
Подставив (8.45) в
(8.44), объединим слагаемые с
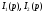 и
и перенесем
в правую часть
перенесем
в правую часть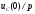 ,
,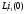 и другие внутренние ЭДС. В результате
получим
и другие внутренние ЭДС. В результате
получим
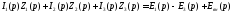 (8.46)
(8.46)
где
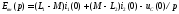
В более общем виде
у-ие (8.46) можно записать так:
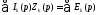 (8.47)
(8.47)
Уравнение (8.47)
представляет собой математическуюзапись
второго закона Кирхгофа в операторной
форме. В состав
 в общем случае входят и внутренние ЭДС.
в общем случае входят и внутренние ЭДС.
12. Первый закон Кирхгофа в операторной форме.
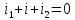
Применив преобразование Лапласса и воспользовавшись тем, что сумма изображений равна изображению сумм, получим, что сумма операторных токов в узле равна 0:
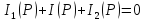
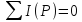
14. Расчет переходных процессов операторным методом в rc контуре при ступенчатом воздействии.
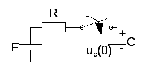
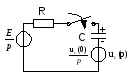
Схема замещения цепи для L-изображений (L- преобразование Лапласа ):
L- изображение токов в контуре
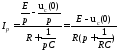
Найденному изображению
согласно таблице соответствий находится
оригинал.
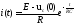
Он определяет закон изменения токов в контуре.
При нахождении L-изображения напряжения на ёмкости следует иметь в виду что оно равно сумме L-изображений напряжения на не заряженной емкости и начального условия.


Используя таблицу соответствия и учитывая линейность обратного преобразования Лапласа находим напряжение на конденсаторе как функция времени.
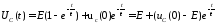

13. Второй закон Кирхгофа в операторной форме.

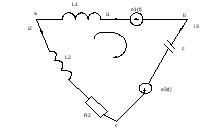
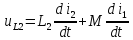
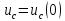
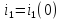
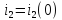
По второму закону Кирхгофа:
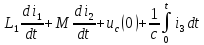 -
-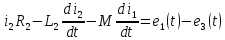 .
.
Каждое из слагаемых заменяем операторным выражением:
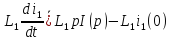 ,
,
 ,
, ,
,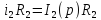
 ,
,
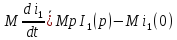 ,
, ,
,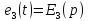
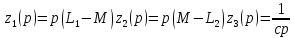
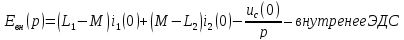
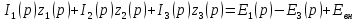
 второй закон
Кирхгофа.
второй закон
Кирхгофа.
В сумму
 в общем случае
входят и внутреннее ЭДС.
в общем случае
входят и внутреннее ЭДС.
15. Расчет переходных процессов операторным методом в параллельном колебательном контуре при ступенчатом воздействии.
Пусть к параллельному колебательному контуру подсоеденены ступенчатые воздействия тока при нулевых начальных условиях
Нарисуем: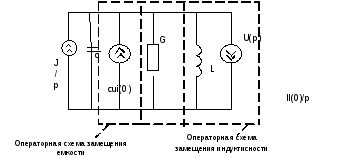
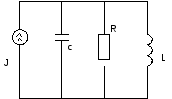
L-изображение
воздействия: Операторное:
Операторное: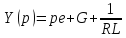
L-изображение
напряжения на зажимах
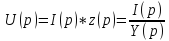
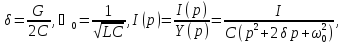
Используя таблицы соответствия находим оригинал:
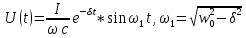
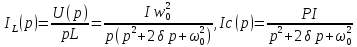
По таблице соответствия находим оригинал токов:

Найденные решения
соответствуют случаю комплексно-сопряженных
полей полинома:
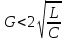
Если воздействие к тому же контуру подведено при ненулевых начальных условиях, то целесообразно использовать схемы замещения реактивных элементов для ненулевых начальных условий, т.е. схемы замещения с источника тока, тогда L-изображения воздействия на контур:

Для нахождения соответствующего оригинала с помощью таблиц следует представить это изображение в виде суммы:

Если
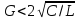 , в результате простого преобразования
находим выражение для напряжения на
контуре в режиме переходных колебаний:
, в результате простого преобразования
находим выражение для напряжения на
контуре в режиме переходных колебаний:

Аналогично могут быть найдены токи в элементах контура.
