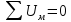- •I. Четырехполюсники.
- •1. Основные определения и классификация четырехполюсников.
- •2. Системы уравнений четырехполюсников.
- •3. Входное сопротивление четырехполюсника при произвольной нагрузке.
- •4. Соединения четырехполюсника.
- •II. Переходные процессы в электрических цепях.
- •6. Переходные процессы в rLc цепи(последовательном контуре).
- •7. Общий случай расчета переходных процессов классическим методом.
- •8. Основные положения операторного метода расчета переходных процессов в электрических цепях.
- •9. Изображение напряжения на индуктивности.
- •11. Закон Ома в операторной форме. Внутренние эдс.
- •12. Первый закон Кирхгофа в операторной форме
- •13. Второй закон Кирхгофа в операторной форме
- •12. Первый закон Кирхгофа в операторной форме.
- •14. Расчет переходных процессов операторным методом в rc контуре при ступенчатом воздействии.
- •13. Второй закон Кирхгофа в операторной форме.
- •15. Расчет переходных процессов операторным методом в параллельном колебательном контуре при ступенчатом воздействии.
- •16. Расчет переходных процессов операторным методом в параллельном колебательном контуре при гармоническом воздействии
- •17. Последовательность расчета пп операторным методом
- •18. Расчет переходных процессов методом переменных состояния.
- •19. Последовательность расчета переходных процессов методом переменных состояния.
- •20. Численный метод решения уравнений состояния динамической цепи.
- •III. Периодические несинусоидальные токи в электрических цепях.
- •1. Основные понятия о несинусоидальных эдс, напряжениях, тока и методах анализа.
- •2. Действующие и средние значения несинусоидальных электрических величин.
- •4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.
- •3. Активная мощность при несинусоидальных напряжении и токе.
- •4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.
- •5. Несинусоидальные кривые с периодической огибающей. Биения
- •7. Высшие гармоники в трехфазных цепях.
- •IV. Цепи (линии) с распределенными параметрами.
- •1. Направляющие сис-мы передачи электроэнергии и их модели.
- •2. Уравнение двухпроводной линии
- •3.Уравнения многопроводных линий
- •4.Расчет процессов в цепях с распределенными параметрами.
- •5.Установившиеся режимы в линиях.
- •V. Нелинейные электрические цепи.
- •1. Нелинейные элементы и их вольтамперные характеристики.
- •2. Последовательное соединение нелинейных элементов.
- •3. Параллельное соединение нелинейных элементов.
- •4. Смешанное соединение нелинейных элементов.
- •5. Статические и дифференциальный сопротивления.
- •6. Замена нелинейного элемента линейным сопротивлением и эдс.
- •VI. Магнитные цепи.
- •2. Закон Ома и законы Кирхгофа для магнитных цепей.
- •3.Расчет неразветвленных магнитных цепей.
- •4. Расчет разветвленных магнитных цепей.
- •5. Магнитные цепи переменного тока.
- •VII. Теория электромагнитного поля.
- •1. Электромагнитное поле и его уравнение в интегральной форме.
- •2. Закон полного тока в дифференциальной форме (первое уравнение максвелла )
- •3. Закон электромагнитной индукции в дифференциальной форме(второе уравнение максвелла)
- •4. Теорема гаусса и постулат максвелла в дифференциальной форме
- •5. Выражение в дифференциальной форме принципов непрерывности магнитного потока и непрерывности электрического тока.
- •8. Уравнение Пуассона и Лапласа для электростатического поля
- •9. Уравнение Максвелла в комплексном виде. Волновое уравнение Гельмгольца
- •11. Вектор Пойнтинга
- •12. Вывод волновых уравнений непосредственно из уравнений Максвелла в дифференциальной форме
- •10. Основные свойства плоских электромагнитных волн
- •13. Численные методы расчета электромагнитных полей. Граничные условия
5. Статические и дифференциальный сопротивления.

Статическое
сопротивление пропорционально tgα
образованной секущей проведенной из
начала координат в рассматриваемую
точку характеристики. 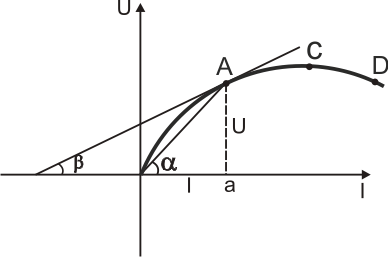
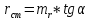
Дифференциальное
сопротивление пропорционально tgβ
образованного касательной в рассматриваемой
точки с осью I:
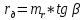
При этом k=v/a,
где v
и а – масштабы напряжений и тока.
Соответственно,
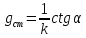 ;
;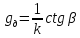 ;
;
Для так называемых
пассивных элементов, т. е, не содержащих
источников энергии, всегда rст
> 0 и gст
> 0, но
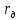 и
и положительны, только когда данная точка
характеристики лежит на ее восходящей
части, и отрицательные, если данная
точка лежит на падающей части
характеристики.
положительны, только когда данная точка
характеристики лежит на ее восходящей
части, и отрицательные, если данная
точка лежит на падающей части
характеристики.
6. Замена нелинейного элемента линейным сопротивлением и эдс.
Предположим, что область работы нелинейного элемента не выходит за пределы участка вольтамперной характеристики, который с достаточной степенью точности можно представить в виде прямой линии (рис. 2.29-Замена нелинейных элементов динамическими сопротивлениями и ЭДС)
Если продолжить линейные участки характеристик нелинейных элементов, то они пересекут ось абсцисс в точках E1 и E2.
Полученные две
ломаные линии могут быть, в соответствии
с ранее рассмотренным методом расчета
нелинейной электрической цепи,
представлены последовательным
соединением источника ЭДС E и динамического
сопротивления ![]() (рис.
2.30,б)
(рис.
2.30,б)
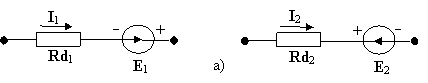
Рис. 2.30. Представление двух типов нелинейности (1 и 2, рис. 2.29) в виде двух линейных цепей (а и б).
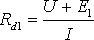 ;
; ![]() ;
;![]() ;
;![]() .
(2.36)
.
(2.36)
После замены нелинейного элемента линейным сопротивлением и ЭДС электрическая цепь рассчитывается как линейная. При этом обязательно должно соблюдаться условие: рабочая точка должна находиться на линейном участке характеристики нелинейного элемента.
VI. Магнитные цепи.
1. Магнитные цепи при постоянных магнитных потоках.
Магнитная цепь- совокупность феррамагнитных тел и воздушных сред,по которым замыкается магнитный поток.
Магнитные цепи являются частью электротехнического устройства и предназначены для создания в заданном объеме магнитного поля нужной интенсивности.
В неразветвленных магнитных цепях поток сечений каждого участка один и тот же.
2. Закон Ома и законы Кирхгофа для магнитных цепей.
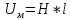 ,
,
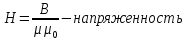 ,
,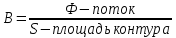 –
индукция
–
индукция
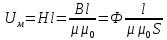 ,
,
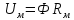 -закон Ома для магнитной цепи,
-закон Ома для магнитной цепи,
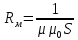 - магнитное сопротивление ,
- магнитное сопротивление ,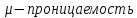 ,
,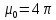 *
*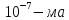 гнитная
постоянная
гнитная
постоянная
Ф= ,
В
замкнутом контуре : Ф=
,
В
замкнутом контуре : Ф=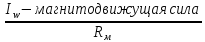
1 закон Кирхгофа
вытекает из принципа непрерывности
линий магнитной индукции: В любом узле
сложной магнитной цепи алгебраическая
сумма магнитных потоков равна 0.
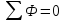
Магнитные потоки направленные к узлу берут со знаком “+”, а выходящие из узла со знаком “-”.
Сумма приходящих к узлу магнитных потоков равна сумме выходящих из узла магнитных потоков.
2 закон Кирхгофа
:В любом
разомкнутом контуре сложной магнитной
цепи алгебраическая сумма магнитных
U
равна сумме
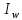 действующих в этом контуре.
действующих в этом контуре.
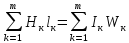 ,
,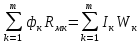
Достоинство этих законов в том, что они помогают провести аналогию между электрическими и магнитными цепями,которая позволяет применять для расчета магнитных цепей те же методы,что и для расчета н.э.ц.
|
Электрическая цепь |
Магнитная цепь |
|
|
Вывод: возможно использование схем замещения для магнитных цепей постоянного магнитного потока в виде графического изображения элементов магнитной цепи подобных элементам электрической цепи.

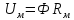
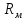 имеет вебер-амперную
хар-ку
имеет вебер-амперную
хар-ку