- •I. Четырехполюсники.
- •1. Основные определения и классификация четырехполюсников.
- •2. Системы уравнений четырехполюсников.
- •3. Входное сопротивление четырехполюсника при произвольной нагрузке.
- •4. Соединения четырехполюсника.
- •II. Переходные процессы в электрических цепях.
- •6. Переходные процессы в rLc цепи(последовательном контуре).
- •7. Общий случай расчета переходных процессов классическим методом.
- •8. Основные положения операторного метода расчета переходных процессов в электрических цепях.
- •9. Изображение напряжения на индуктивности.
- •11. Закон Ома в операторной форме. Внутренние эдс.
- •12. Первый закон Кирхгофа в операторной форме
- •13. Второй закон Кирхгофа в операторной форме
- •12. Первый закон Кирхгофа в операторной форме.
- •14. Расчет переходных процессов операторным методом в rc контуре при ступенчатом воздействии.
- •13. Второй закон Кирхгофа в операторной форме.
- •15. Расчет переходных процессов операторным методом в параллельном колебательном контуре при ступенчатом воздействии.
- •16. Расчет переходных процессов операторным методом в параллельном колебательном контуре при гармоническом воздействии
- •17. Последовательность расчета пп операторным методом
- •18. Расчет переходных процессов методом переменных состояния.
- •19. Последовательность расчета переходных процессов методом переменных состояния.
- •20. Численный метод решения уравнений состояния динамической цепи.
- •III. Периодические несинусоидальные токи в электрических цепях.
- •1. Основные понятия о несинусоидальных эдс, напряжениях, тока и методах анализа.
- •2. Действующие и средние значения несинусоидальных электрических величин.
- •4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.
- •3. Активная мощность при несинусоидальных напряжении и токе.
- •4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.
- •5. Несинусоидальные кривые с периодической огибающей. Биения
- •7. Высшие гармоники в трехфазных цепях.
- •IV. Цепи (линии) с распределенными параметрами.
- •1. Направляющие сис-мы передачи электроэнергии и их модели.
- •2. Уравнение двухпроводной линии
- •3.Уравнения многопроводных линий
- •4.Расчет процессов в цепях с распределенными параметрами.
- •5.Установившиеся режимы в линиях.
- •V. Нелинейные электрические цепи.
- •1. Нелинейные элементы и их вольтамперные характеристики.
- •2. Последовательное соединение нелинейных элементов.
- •3. Параллельное соединение нелинейных элементов.
- •4. Смешанное соединение нелинейных элементов.
- •5. Статические и дифференциальный сопротивления.
- •6. Замена нелинейного элемента линейным сопротивлением и эдс.
- •VI. Магнитные цепи.
- •2. Закон Ома и законы Кирхгофа для магнитных цепей.
- •3.Расчет неразветвленных магнитных цепей.
- •4. Расчет разветвленных магнитных цепей.
- •5. Магнитные цепи переменного тока.
- •VII. Теория электромагнитного поля.
- •1. Электромагнитное поле и его уравнение в интегральной форме.
- •2. Закон полного тока в дифференциальной форме (первое уравнение максвелла )
- •3. Закон электромагнитной индукции в дифференциальной форме(второе уравнение максвелла)
- •4. Теорема гаусса и постулат максвелла в дифференциальной форме
- •5. Выражение в дифференциальной форме принципов непрерывности магнитного потока и непрерывности электрического тока.
- •8. Уравнение Пуассона и Лапласа для электростатического поля
- •9. Уравнение Максвелла в комплексном виде. Волновое уравнение Гельмгольца
- •11. Вектор Пойнтинга
- •12. Вывод волновых уравнений непосредственно из уравнений Максвелла в дифференциальной форме
- •10. Основные свойства плоских электромагнитных волн
- •13. Численные методы расчета электромагнитных полей. Граничные условия
5.Установившиеся режимы в линиях.
При действии на входе линейной цепи с распределенными параметрами установившегося синусоидального сигнала U и I в любой точке линии так же будут синусоидальными, одной частоты с отличающимися амплитудами и начальными фазами.
Задача расчета процессов линии сводится к нахождению распределения амплитуд и фаз синусоидальных U и I в зависимости от координаты.
В символической форме записи телеграфные уравнения сводятся к системе обыкновенных дифференциальных уравнений.
-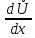 =
(r0+
jωL0)İ=
=
(r0+
jωL0)İ=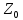 İ
-
İ
-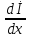 =
(g0+
jωC0)
=
(g0+
jωC0)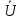 =
=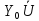
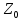 ,
,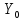 -
полные погонные сопротивления и
проводимость
-
полные погонные сопротивления и
проводимость
Решение
уравнений:
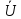 (x)=
(x)=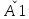 е-γх+
е-γх+
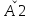 еγх
еγх
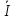 (x)=
(x)=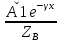 –
–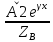 ,
гдеγ=
,
гдеγ=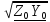 -
комплексная постоянная распределения
на частоте ω,
-
комплексная постоянная распределения
на частоте ω,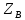 =
=
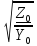 -
комплексное волновое сопротивление на
частоте ω
-
комплексное волновое сопротивление на
частоте ω
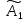 ,
,
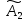 -
комплексные коэффициенты,зависящие от
граничных условий.
-
комплексные коэффициенты,зависящие от
граничных условий.
Комплексы
прямой и обратной волн:
 (x)
=
(x)
=
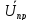 (х)+
(х)+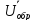 (х)
(х)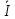 (x)
=
(x)
=
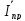 (х)+
(х)+ (х)
(х)
Волновое сопротивление и постоянная распространения определяет характер процессов в линии при синусоидальном воздействии и носит название вторичных параметров. Первичные параметры линии : r0, g0, c0, l0… Постоянная распространения включает в себя коэффициенты затухания α и коэффициент фазы β.
γ=
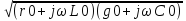 =α+β
=α+β
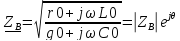
Вторичные
параметры завися от типа линии передачи
и использованной частоты.Вторичные
параметры линии постоянного тока: γ=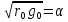
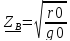
Для
линии без потерь r0=0,
g0=
0: γ=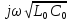 α=0
β=
α=0
β=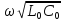 ,
,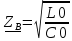
 =
=
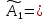 A1*
A1*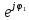
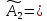 A2*
A2*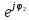 , u(x,t)=A1
, u(x,t)=A1
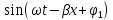 +
A2
+
A2
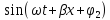
i(x,t)=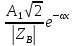
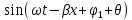 -
-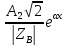
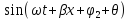
Фиксированные
точки линии Хн
напряжения представляют собой
синусоидальную функцию времени.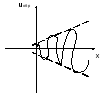
u(xн,t)=A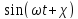
Если
рассмотреть напряжение вдоль линии в
фиксированный момент времени t1
,то оно представляет собой сумму
затухающих синусоидальных функций.Одну
называют прямой волной напряжения,вторую-обратной
волной напряжения.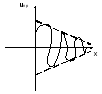
Для
линии без потерь при α=0 и момента времени
t2
амплитуда синусоиды не изменяется.а
начальная фаза увеличивается на ω∆t.
Кривая как бы передвинулась на значение
∆х = ω∆t/β.
Синусоидальное
распределение напряжения (тока) в
пространстве по координате х называют
бегущей волной. Основные характеристики
бегущей волны: фазовая скорость и длина
волны.Фазовая скорость-скорость
перемещения точки с неизвестным фазовым
углом. Vф=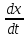 =
=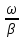
Длина волны λ – расстояние,на которое распространяется бегущая волна за период Т: λ= Vф*Т
Для обратной волны фазовая скорость отрицательна.С энергетической точки зрения важно распределение вдоль линии действительных значений напряжения и тока при известной нагрузке.
Для
начала линии х=0
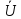 (x)=
(x)=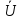 chγx
-
chγx
-
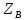 I1
sinγx
I1
sinγx
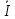 (x)=-
(x)=-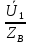 shγx
+
shγx
+
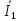 chγx
chγx
Относительно
конца линий:
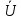 (y)=
(y)= chγy
+
chγy
+
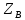 shγy
shγy
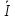 (x)=-
(x)=-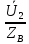 shγy
+
shγy
+
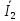 chγy.
Для линии без потерь γ= jβ
chγy.
Для линии без потерь γ= jβ
Введем
комплексное сопротивление нагрузки
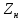 =
= .
.
Входное
сопротивление линии в произвольной
точке.
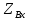 (y)=
(y)=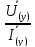
Сопротивление полученных выражений с общим решением для линий без потерь приврдит к выводу,что реализован режим бегущей волны.
Действующие значения выражений напряжения и тока не изменяются вдоль линии.Такой режим работы называют режимом согласования нагрузки с волновым сопротивлением линии.
 RΩ=
RΩ=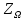 - для любой точки линии
- для любой точки линии
Для
режима разомкнутой линии
 (y)=
(y)=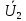 cosβy
cosβy
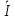 (y)=-
(y)=-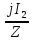 sinβy
sinβy
Распределение
модулей действующих значений I(y)=-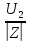 sinβy
sinβy
Такое распределение действующих значений вдоль линии называется режимом стоячих волн.
u(y,t)=U2msinωtcosβy i(y,t)=I2mcosωtsinβy
В фиксируемой точке линии получаем синусоидальные U и I ,имеющие фазовый сдвиг П/2.Если в различные моменты времени зафиксировать картины распределения U и I вдоль линии,то получим синусоидальные кривые,у которых нулевые точки неподвижны,а изменяется синусоида.
В режиме размыкания выхода активная мощность =0 в любой точке линии.Входное сопротивление линии имеет реактивный характер.
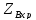 =-jZBctgβy
=-jZBctgβy
С
энергетической точки зрения оптимальным
является режим согласованной нагрузки,
поскольку в других режимах имеются
отрезки линии с повышенным напряжением
и отрезки с большим значением тока.
Повышение напряжения затрат на улучшение
изоляции для снижения сопротивления
утечки и предотвращения пробоя. Большое
значение тока приводит к необходимости
увеличения сечения проводников
добавочному расходу металла. В реальных
линиях предпринимаются меры по приближению
режима работы линии к согласованному
с использованием различных согласующих
устройств.