
- •I. Четырехполюсники.
- •1. Основные определения и классификация четырехполюсников.
- •2. Системы уравнений четырехполюсников.
- •3. Входное сопротивление четырехполюсника при произвольной нагрузке.
- •4. Соединения четырехполюсника.
- •II. Переходные процессы в электрических цепях.
- •6. Переходные процессы в rLc цепи(последовательном контуре).
- •7. Общий случай расчета переходных процессов классическим методом.
- •8. Основные положения операторного метода расчета переходных процессов в электрических цепях.
- •9. Изображение напряжения на индуктивности.
- •11. Закон Ома в операторной форме. Внутренние эдс.
- •12. Первый закон Кирхгофа в операторной форме
- •13. Второй закон Кирхгофа в операторной форме
- •12. Первый закон Кирхгофа в операторной форме.
- •14. Расчет переходных процессов операторным методом в rc контуре при ступенчатом воздействии.
- •13. Второй закон Кирхгофа в операторной форме.
- •15. Расчет переходных процессов операторным методом в параллельном колебательном контуре при ступенчатом воздействии.
- •16. Расчет переходных процессов операторным методом в параллельном колебательном контуре при гармоническом воздействии
- •17. Последовательность расчета пп операторным методом
- •18. Расчет переходных процессов методом переменных состояния.
- •19. Последовательность расчета переходных процессов методом переменных состояния.
- •20. Численный метод решения уравнений состояния динамической цепи.
- •III. Периодические несинусоидальные токи в электрических цепях.
- •1. Основные понятия о несинусоидальных эдс, напряжениях, тока и методах анализа.
- •2. Действующие и средние значения несинусоидальных электрических величин.
- •4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.
- •3. Активная мощность при несинусоидальных напряжении и токе.
- •4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.
- •5. Несинусоидальные кривые с периодической огибающей. Биения
- •7. Высшие гармоники в трехфазных цепях.
- •IV. Цепи (линии) с распределенными параметрами.
- •1. Направляющие сис-мы передачи электроэнергии и их модели.
- •2. Уравнение двухпроводной линии
- •3.Уравнения многопроводных линий
- •4.Расчет процессов в цепях с распределенными параметрами.
- •5.Установившиеся режимы в линиях.
- •V. Нелинейные электрические цепи.
- •1. Нелинейные элементы и их вольтамперные характеристики.
- •2. Последовательное соединение нелинейных элементов.
- •3. Параллельное соединение нелинейных элементов.
- •4. Смешанное соединение нелинейных элементов.
- •5. Статические и дифференциальный сопротивления.
- •6. Замена нелинейного элемента линейным сопротивлением и эдс.
- •VI. Магнитные цепи.
- •2. Закон Ома и законы Кирхгофа для магнитных цепей.
- •3.Расчет неразветвленных магнитных цепей.
- •4. Расчет разветвленных магнитных цепей.
- •5. Магнитные цепи переменного тока.
- •VII. Теория электромагнитного поля.
- •1. Электромагнитное поле и его уравнение в интегральной форме.
- •2. Закон полного тока в дифференциальной форме (первое уравнение максвелла )
- •3. Закон электромагнитной индукции в дифференциальной форме(второе уравнение максвелла)
- •4. Теорема гаусса и постулат максвелла в дифференциальной форме
- •5. Выражение в дифференциальной форме принципов непрерывности магнитного потока и непрерывности электрического тока.
- •8. Уравнение Пуассона и Лапласа для электростатического поля
- •9. Уравнение Максвелла в комплексном виде. Волновое уравнение Гельмгольца
- •11. Вектор Пойнтинга
- •12. Вывод волновых уравнений непосредственно из уравнений Максвелла в дифференциальной форме
- •10. Основные свойства плоских электромагнитных волн
- •13. Численные методы расчета электромагнитных полей. Граничные условия
I. Четырехполюсники.
1. Основные определения и классификация четырехполюсников.
Четырехполюсник — это обобщенное наименование электрической цепи, рассматриваемой по отношению к четырем ее зажимам.
Трансформатор, линию передачи энергии, мостовую схему и т. п. можно рассматривать как четырехполюсники.
Принято изображать четырехполюсник в виде прямоугольника с выходящими из него концами (полюсами) тп и pq. Если четырехполюсник содержит источники электрической энергии, то в прямоугольнике ставят букву А (активный); если буква А отсутствует, то это значит, что четырехполюсник пассивный.

В общем, практически мало распространенном случае рабочими парами зажимов четырехполюсника могут быть три пары зажимов. (например, пары mn, рm и pq). В этом случае режим им работы четырехполюсника определялся бы тремя независимыми уравнениями, в которые входили бы три независимых напряжения (что следует из второго закона Кирхгофа) между упомянутыми парами зажимов и тремя независимыми токами (что следует из первого закона Кирхгофа). На практике четырехполюсник обычно работает в режиме, когда одна пара зажимов, например, mn, является входной, а другая пара, например pq — выходной. Четырехполюсник, у которого рабочими являются две пары зажимов, называют проходным.
Входной ток обозначают
 входное напряжение—
входное напряжение— ;
ток и напряжение на выходе —
;
ток и напряжение на выходе — и
и .
.
Четырехполюсник является передаточным звеном между источником питания и нагрузкой. К входным зажимам тп, как правило, присоединяют источник питания, к выходным зажимам pq — нагрузку.
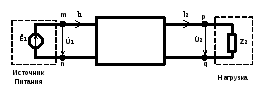
Предполагается, что нагрузка четырехполюсника и напряжение на входе при работе четырехполюсника в качестве связующего звена могут изменяться, но схема внутренних соединений четырехполюсника и сопротивления в ней остаются неизменными.
Классификация четырехполюсников:
Линейные и нелинейные (ВАХ элементов четырехполюсника)
Пассивные и активные (наличие ЭДС)
С сосредоточенными параметрами и распределенными параметрами.
Симметричные и не симметричные (A=D, A≠D)
Эквивалентные и не эквивалентные.
2. Системы уравнений четырехполюсников.
Четырехполюсник
характеризуется двумя напряжениями
 и
и и двумя токами
и двумя токами и
и .
Любые две величины из четырех можно
определить через остальные. Так как
число сочетаний из четырех по два равно
шести, то возможны следующие шесть форм
записи уравнений пассивного
четырехполюсника:
.
Любые две величины из четырех можно
определить через остальные. Так как
число сочетаний из четырех по два равно
шести, то возможны следующие шесть форм
записи уравнений пассивного
четырехполюсника:
A–форма:


B-форма:


Y-форма:
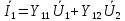

Z-форма:


H-форма:


G-форма:

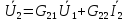
Обратим внимание на попарную инверсию Y- и Z-форм, А- и В-форм, Н- и G-форм.



Исторически сложилось так, что для А-формы (ее будем считать основной) положительные направления для токов и напряжений соответствуют рис. 1, для Y-, Z-, H-G-форм — рис. 2, для B-формы — рис. 3.
Обратим внимание
на то, что ток
 на рис. 2 направлен противоположно
току
на рис. 2 направлен противоположно
току на
рис. 1.
на
рис. 1.
На рис. 3
 и
и изменили
направление по сравнению с токами
изменили
направление по сравнению с токами и
и на
рис. 1.
на
рис. 1.
3. Входное сопротивление четырехполюсника при произвольной нагрузке.
В случае несимметричного четырехполюсника (A≠D) рассматривают два характеристических сопротивления— Zc1 и Zc2, где Zc1— входное сопротивление со стороны зажимов mn, когда нагрузка подключена к зажимам pq и равна Zc2 (рис. 1):


ZC2
— входное сопротивление со стороны
зажимов pq,
когда нагрузка ZC1
подключена
к зажимам тп
(рис. 2);
при этом коэффициенты
А и D меняются
местами:

Совместно решая
уравнения (1) и (2) получим: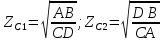
Учитывая, что


 получим:
получим:

Если четырехполюсник симметричен (A=D), то
 где
Zc
равно входному сопротивлению
четырехполюсника, когда он нагружен
на Zc
(рис. 3).
где
Zc
равно входному сопротивлению
четырехполюсника, когда он нагружен
на Zc
(рис. 3).В теории цепей иногда пользуются понятием повторного сопротивления четырехполюсника ZП0B. Под ним понимают входное сопротивление со стороны зажимов тп, если к выходным зажимам pq присоединено ZПОВ. Из первой формулы, заменив в ней Zc1 и Zc2 на ZПОВ, получим

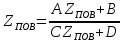
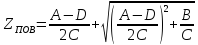
Если четырехполюсник симметричный (A = D), то ZП0B =
 ,
т. е. оно совпадает с характеристическим
сопротивлениемZc.
Сопротивление ZПОВ
называют повторным потому, что оно
повторяет сопротивление нагрузки
на выходе четырехполюсника.
,
т. е. оно совпадает с характеристическим
сопротивлениемZc.
Сопротивление ZПОВ
называют повторным потому, что оно
повторяет сопротивление нагрузки
на выходе четырехполюсника.
