Lektsia-7

4.5. Происхождение главного магнитного поля Земли

После открытий палеомагнетизма практически ни у кого не вызывало сомнения, что процесс генерации ГМПЗ – это результат квазистационарных магнитогидродинамических течений в жидком земном ядре. Магнитная гидродинамика – это раздел физики, изучающий течения проводящих сплошных сред (жидкостей, газов и плазмы) в магнитных полях. Наиболее важные пионерские исследования в теории магнитогидродинамических (МГД) процессов принадлежат Лармору, Каулингу и Альфвену. Лармор в 1919 году первым попытался объяснить магнитные поля Солнца течениями плазмы в конвективной зоне Солнца. Ему принадлежит идея о гидромагнитном динамо (ГД). Вначале теория МГД-процессов развивалась преимущественно астрофизиками, которые быстро поняли, какую важную роль должны играть магнитные поля при движении плазмы в атмосферах звезд, в скоплениях протозвездного вещества и даже в межзвездном пространстве. В 1934 г. Каулинг в развитие идеи Лармора опубликовал работу, посвященную теории солнечного динамо, в которой, в частности, доказал, что осесимметричные течения проводящей жидкости или плазмы не могут генерировать осесимметричное (дипольное) магнитное поле. Этот результат в дальнейшем получил названия «теорема Каулинга» или «теорема антидинамо». Наконец, в 1942 г. Альфвен теоретически обосновал возможность возникновения и распространения в замагниченных жидкостях, газах и плазме поперечных волн. Собственно именно Альфвен и ввел термин «магнитная гидродинамика».

Выведем основное уравнение магнитной гидродинамики. Рассмотрим систему уравнений Максвелла для случая хорошо проводящей сплошной среды, в которой имеется отличное от нуля поле скоростей .

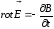, (1)

, (2)

, (3)

. (4)

В правой части уравнения (2) мы пренебрегли токами смещения, которые малы в сравнении с токами проводимости . В правой части уравнения (3) положили равной нулю объемную плотность несвязанных электрических зарядов. В проводящей среде несвязанные заряды существовать не могут. К уравнениям (1)–(4) нужно добавить закон Ома в дифференциальной форме:

, (5)

где – электропроводность среды (удельная электрическая проводимость). В движущейся в магнитном поле проводящей среде помимо обычного тока проводимости возникает еще так называемый ток Холла .

Из уравнений (1)–(5) исключим электрическое поле. Для этого возьмем ротацию от второго уравнения Максвелла.

Отсюда получаем так называемое уравнение индукции – основное уравнение магнитной гидродинамики:

. (6)

Изменения магнитного поля во времени определяются двумя противоположными по своему действию процессами: генерацией этого поля – первый справа член в (6) и диссипацией поля – второй справа член в (6). В зависимости от того, какой из этих членов в уравнении (6) превалирует, магнитное поле в системе будет нарастать или затухать. Пусть характерный линейный размер системы , характерная скорость течений . Тогда отношение генерирующего члена к диссипативному члену по порядку величины равно:

.

Безразмерная величина называется магнитным числом Рейнольдса для данной МГД–системы. Если , то течения жидкости способны, в принципе, генерировать нарастающее до определенного предела магнитное поле. Если же 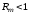, то процесс генерации невозможен из-за сильного омического затухания.

Для дальнейшего полезно рассмотреть действие каждого из членов правой части уравнения индукции (6) в отдельности. Вначале рассмотрим ситуацию, когда поле скоростей равно нулю. В этом случае уравнение индукции сводится к уравнению диффузии магнитного поля:

. (7)

Величина имеет смысл коэффициента магнитной диффузии. Характерное время диффузии (распада) поля, которое не поддерживается источниками, равно . Рассмотрим, к примеру, земное ядро. Электропроводность расплава земного ядра из физических и теоретических соображений оценивают величиной порядка 3∙10⁵ См/м, толщина жидкой части ядра равна 2,3∙10⁶ м. Тогда характерное время распада геомагнитного поля, если оно не будет поддерживаться источниками, равно . Другое дело Метагалактика. Ее линейные размеры порядка 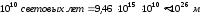. Магнитное поле в ней может существовать безо всякого поддержания в течение времени, превышающей возраст Метагалактики, даже если электропроводность межгалактического пространства ничтожна.

Предположим дальше, что электропроводность замагниченной среды очень велика, так что диффузией магнитного поля можно пренебречь. Тогда

. (8)

Рассмотрим ситуацию, когда в постоянном магнитном поле с постоянной угловой скоростью вращается идеально проводящая среда. Задачу о генерации поля в этом случае удобно решать в цилиндрических координатах (). Исходное магнитное поле направим вдоль оси s, , а вектор угловой скорости направим вдоль оси z, тогда . Магнитное поле представим в виде суммы и линеаризуем правую часть (8), пренебрегая вторичными полями.

.

Далее

.

В результате взаимодействия вращающейся в магнитном поле электропроводной жидкости (или плазмы) возникает азимутальное магнитное поле 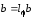, изменение со временем которого описывается уравнением

, или .

Идеально проводящая вращающаяся жидкость захватывает силовые линии магнитного поля и накручивает их вокруг своей оси вращения. В магнитной гидродинамике говорят, что магнитное поле вморожено в идеально проводящую жидкость. Рост азимутального поля безграничен.

В реальности же электропроводность конечна и с ростом азимутального поля возрастает его диссипация. Согласно уравнению (6) имеем

.

Рост генерируемого поля прекратится, как только члены справа в этом уравнении по порядку величины станут одинаковыми, т.е.

.

Отсюда видим, что , где – магнитное число Рейнольдса.

Для решения задачи о генерации магнитного поля в земном ядре к уравнению (6) необходимо еще добавить уравнения движения жидкости – уравнения Навье-Стокса:

, (9)

где – плотность жидкости, – поле ее скоростей и 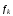– объемная плотность сил (Н/м³), действующих на жидкость. К числу последних относятся:

1) магнитная сила ;

2) кориолисова сила , 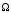– угловая скорость вращения Земли;

3) архимедова сила , – вариации плотности, – ускорение силы тяжести;

4) сила давления 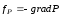, где P – давление, включая магнитное давление ;

5) сила вязкости , где – динамический коэффициент вязкости.

Как показывают оценки физических условий в жидком земном ядре, вязкостью в основном объеме ядра (но не на границе с мантией) можно пренебречь. Магнитная сила в основном тормозит течения, кориолисова сила придает течениям азимутальный характер, сила давления – это поверхностная сила и ее, как правило, можно исключить из рассмотрения. Движущей силой конвекции является архимедова сила, которая возбуждает необходимое для генерации поле скоростей. Согласно экспериментальным данным с расплавами железа при давлениях и температуре, которые имеют место в земном ядре, а также теоретическим термодинамическим расчетам тепловой конвекции в земном ядре возникнуть не может, поскольку адиабатический градиент температуры (рост температуры за счет давления) превышает градиент температуры плавления. Другими словами, земное ядро с термодинамической точки зрения стратифицировано. Поэтому было предположено, что вариации плотности, следовательно, и конвекция в ядре обусловлены процессом химико-плотностной дифференциации вещества Земли. Тяжелая фракция, в состав которой входит железо, из мантии опускается в земное ядро, на поверхности твердого субъядра происходит кристаллизация железа с освобождением легких фракций (кислорода, серы, кремния и пр.), которые всплывают к поверхности жидкого ядра. Гипотеза химико-плотностной дифференциации в настоящее время является основной гипотезой, с помощью которой удается объяснить основные черты эволюции не только глубоких недр, но и всей Земли в целом.

Совместное решение системы уравнений (6) и (9) представляет собой практически неразрешимую задачу по двум причинам. Во-первых, велики неопределенности в конкретном механизме, который продуцирует вариации плотности в ядре, а также в оценках таких физических параметров, как вязкость ядра, электропроводность нижней мантии и внутреннего субъядра, которые играют существенную роль в постановке граничных условий на границах раздела «ядро–мантия» и «жидкое ядро–твердое ядро». Во-вторых, определенные трудности возникают и в процессе приведения системы уравнений (6) и (9) к виду, удобному для численного интегрирования. Дело в том, что задача о генерации геомагнитного поля является существенно трехмерной, к тому же должна решаться в сферической системе координат. Задача о гидромагнитном динамо относится к тому типу задач теоретической физики, для которых уже простое доказательство существования ненулевого решения является нетривиальным.

В силу всех этих причин задача о гидромагнитном динамо Земли в настоящее время решена только в кинематической постановке: для заданного поля скоростей найдены незатухающие решения для магнитного поля.

Поскольку задача ГД рассматривается в сферических координатах, то целесообразно и удобно и магнитное поле, и поле скоростей представить в виде суммы двух взаимно перпендикулярных составляющих – полоидальной (p) и азимутальной (). Полоидальная компонента – это сумма радиальной и меридиональной компонент.

Архимедова сила продуцирует меридиональные скорости. Кориолисова сила эти скорости заворачивает по азимуту. Главное же состоит в том, что если в земном ядре имеет место конвекция, т.е. происходит обмен массами между внешними и внутренними частями ядра, то из закона сохранения вращательного импульса немедленно следует, что внутренние части ядра должны вращаться быстрее мантии, а внешние – медленнее. Сама Земля вращается с запада на восток. Западный дрейф (на запад!) фокусов вековых вариаций геомагнитного поля свидетельствует о том, что внешние приэкваториальные области земного ядра, где и генерируются эти вариации, вращаются медленнее мантии. Принимая скорость западного дрейфа равной 0,2 град/год, получаем оценку азимутальной скорости в земном ядре

.

Полоидальные скорости в ядре как минимум на порядок меньше.

Рассмотрим генерирующий член в уравнении (6).

(10)

Последний член в (10) равен нулю. Третий справа член в (10) генерирует преимущественно азимутальное магнитное поле за счет вытягивания силовых линий полоидального поля дифференциальным вращением земного ядра. Величина полоидального поля в земном ядре примерно в 8 раз (это 2³) больше, чем у поверхности Земли. Следовательно, . Тогда

.

Второй справа член, собственно говоря, и является генерирующим членом: полоидальные скорости из сильного азимутального поля вытягивают вторичное полоидальное поле. Наконец, первый член – это эффект второго порядка малости по сравнению с только что рассмотренным членом.

Процесс генерации поля – это существенно нестационарный процесс. Некоторое время идет процесс нарастания поля и соответствующего нарастания поля При этом возрастает магнитная сила

,

которая тормозит конвективные течения . Это приведет к уменьшению поля и к соответствующему уменьшению поля . Магнитная сила станет меньше, конвекция усилится, и все начнется сначала. Наблюдаемое на поверхности Земли полоидальное поле должно испытывать колебания во времени.

Примерно на таком уровне, как представлено выше, задачу о генерации геомагнитного поля понимали и представляли в 1940–1960 гг. такие известные физики, геофизики и астрофизики как Каулинг, Буллард, Эльзассер, Френкель, Паркер и другие. Однако до 1964 года не было найдено ни одного теоретического решения этой задачи. Были только определены условия, при которых гидромагнитное динамо невозможно, т.е. доказаны так называемые теоремы «антидинамо».

В 1964 г. С.И. Брагинский опубликовал четыре работы (две в ЖЭТФ и две в журнале «Геомагнетизм и аэрономия»), в которых представил аналитическое решение проблемы динамо и приложения этих решений для Земли. Суть его подхода заключалась в асимтотическом разложении магнитных полей и полей скорости по малому параметру 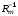в предположении, что электропроводность земного ядра достаточно высока (). Азимутальное поле у Брагинского генерируется дифференциальным вращением, а полоидальное – несимметричным по азимуту полем полоидальных скоростей. Зависимость скоростей от азимута является необходимым условием процесса генерации незатухающего (точнее, осциллирующего) симметричного по азимуту полоидального поля (типа поля диполя).

Следующим важным шагом в развитии теории ГД стали работы немцев Штеенбека, Краузе и Рэдлера, опубликованные в 1966 году, в которых они показали, что турбулентность замагниченной жидкости при условии преобладания в турбулентном потоке гиротропности одного знака (правого или левого кручения вихрей) способна генерировать магнитное поле.

Ламинарный поток электропроводной жидкости создает магнитное поле, перпендикулярное потоку. Это показано на рисунке.

Вихрь же, как следует из второго рисунка, способен создать магнитное поле, параллельное или антипараллельное основному потоку в зависимости от ориентации вихря..

Характеристикой ориентации вихря служит гиротропность – скалярное произведение . На рисунке представлен случай, когда > 0. В этом случае параллельно , которое, в свою очередь, параллельно . В общем случае средняя по объему гиротропность турбулентного потока равна нулю, но действие внешних сил, например, силы Кориолиса, может привести к тому, что в турбулентном потоке будут преобладать только правовинтовые, или только левовинтовые вихри. Тогда и получится, что вдоль главного потока турбулентной конвекции будет создаваться магнитное поле. Этот, доселе неизвестный эффект, авторами был назван α–эффектом. Чуть позже он был подтвержден в лабораторных экспериментах.

В 1970–1990-х годах теоретики насчитали массу самых разных вариантов ГД, большую часть которых можно отнести к двум типам динамо: α²–динамо и αω–динамо. α²–динамо – это когда и азимутальные, и полоидальные магнитные поля генерируются α–эффектом. αω–динамо – это когда азимутальное поле генерируется дифференциальным вращением, а полоидальное – α–эффектом. Динамо Брагинского по этой классификации представляет собой αω–динамо. Теоретические расчеты Брагинского очень неплохо объясняют весь спектр вековых вариаций геомагнитного поля, начиная от основного колебания с периодом порядка 10⁴ лет и кончая так называемыми 60-летними вариациями. Наклон оси геомагнитного диполя к оси вращения Земли теория Брагинского также объясняет.

Инверсии геомагнитного поля – это отдельный вопрос. Может быть проще было придумать теорию этого явления, если бы частота геомагнитных инверсий хотя бы приблизительно сохранялась. Однако согласно данным палеомагнетизма этого не наблюдается, поэтому остается только строить гипотезы относительно причин, по которым почти случайно в геологическом прошлом изменялся знак средней гиротропности полоидальных течений. Хорошей корреляции частоты инверсий с какими-либо геофизическими процессами, документированными в той или иной форме в изученной осадочной толще земной коры, не обнаружено.

В заключение этого раздела имеет смысл подробнее остановиться на силе Кориолиса , которая пропорциональна угловой скорости вращения системы координат, в которой работает ГД, и заворачивает все полоидальные течения по азимуту. Сила Кориолиса, таким образом, способна обеспечить полоидальной конвекции гиротропность, Если конвекция будет несимметрична, то несимметричной будет и гиротропность. Убедиться в том, насколько важна роль этой силы в процессе генерации магнитного поля, можно на следующих примерах.

Конвективная зона Солнца имеет толщину порядка 10⁸ м, дифференциальное вращение в конвективной зоне имеет место и непосредственно наблюдается, магнитное число Рейнольдса для азимутальных течений порядка 10³–10⁴. Поэтому в конвективной зоне Солнца генерируются азимутальные поля интенсивности до 1 Тл. Скорость конвекции тоже велика, а вот полоидальное поле Солнца невелико, порядка земного – 10^–4 Тл, к тому же дипольность его выражена значительно слабее, чем земного поля. Это связано с тем, что угловая скорость вращения Солнца вокруг своей оси в 30 раз меньше угловой скорости вращения Земли. Поэтому кориолисова сила не в состоянии полностью упорядочить по гиротропности турбулентность в конвективной зоне Солнца.

Другим примером является Венера, внутреннее строение которой должно быть подобно внутреннему строению Земли. А вот магнитное поле Венеры очень слабое и совсем не дипольное. Объяснить это можно только тем, что Венера в настоящее время практически не вращается вокруг своей оси. Конвекция в ее ядре есть, а генерации поля нет.

Относительно еще одной планеты земной группы – Марса – можно предположить, что заметного собственного магнитного поля у него нет по той причине, что конвекция в его ядре (а также и в мантии) к настоящему времени практически прекратилась.

Планеты–гиганты (Юпитер, Сатурн, Уран и Нептун) обладают весьма заметными собственными магнитными полями. Если геомагнитное поле на экваторе порядка 31000 нТл, то на экваторе Юпитера оно порядка 430000 нТл, т.е. более чем на порядок выше, чем у Земли. Сатурн и Уран имеют экваториальные поля порядка 22000–23000 нТл, а Нептун – порядка 13000 нТл. Таким образом, получается, что самым большим магнитным полем в Солнечной системе обладает Юпитер.

Собственные магнитные поля звезд самые различные по своей величине. У звезд главной последовательности (типа нашего Солнца) средние поля порядка Тл, у белых карликов – порядка Тл, а вот у нейтронных звезд – порядка Тл и выше.

Рассмотрим, каким образом образуются такие мощные магнитные поля на конечной стадии эволюции звезд. После выгорания всего термоядерного топлива звезда типа Солнца может превратиться в белый карлик, сжавшись под действием собственной гравитации до радиуса примерно в 100 раз меньше исходного. Магнитный поток при этом сжатии должен сохраняться, т.е. где – индукция магнитного поля, – площадь поперечного сечения звезды, – ее радиус. Пусть для примера начальный радиус звезды равен начальное магнитное поле в недрах звезды равно Тл (как у Солнца). Тогда из условия сохранения магнитного потока в процессе гравитационного сжатия звезды получаем

Некоторые звезды в конечной стадии своей эволюции превращаются в нейтронные звезды, радиус которых порядка 10–20 км, т.е. их первоначальный радиус уменьшается примерно в раз. В этом случае, как следует из приведенных выше расчетов, магнитное поле нейтронной звезды может достигнуть величины порядка Тл и выше. В таких магнитных полях работают уже законы не классической, а квантовой физики и общей теории относительности.

67