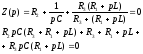Kursovaya_Amirov
.docxФедеральное государственное автономное
образовательное учреждение
высшего профессионального образования
«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
______________________________________________
институт
_________________________________________________________________
кафедра
КУРСОВАЯ РАБОТА
____________________________________________________
тема проекта (работы)
_________________________________________________________________________
____________________________________________________
Руководитель ________ _____________
подпись, дата инициалы, фамилия
Студент ____________________ ________ _____________
номер группы, зачетной книжки подпись, дата инициалы, фамилия
Абакан 2014
ЗАДАНИЕ 1
1. Выбрать схему цепи в (соответствии с номером студента по списку). Для схемы, получившейся после замыкания всех ключей, выполнить расчет токов в установившемся режиме, если на входе цепи задано несинусоидальное напряжение амплитудой 311 В. Считать его получившимся после однополупериодного выпрямления
2. Рассчитать и построить графики токов во всех ветвях. При разложении в ряд Фурье использовать постоянную составляющую и две гармоники
3. Используя программу EWB, смоделировать заданные цепи и получить осциллограммы токов во всех ветвях схемы.
Вариант 2.
рис. 1.1
После замыкания всех ключей (рис. 1.1) начинаем расчет токов. Для этого выполним разложение несинусоидального напряжения в ряд Фурье.
Рассчитаем гармонические составляющие токов в ветвях схемы.
1)Нулевая гармоника (постоянная составляющая):
Составим схему для нулевой гармоники (катушку заменяем закороткой, конденсатор разрывом):
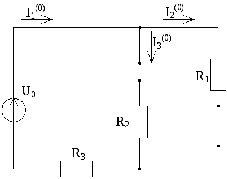
рис. 1.2
Определим токи в ветвях схемы:
-
Первая гармоника:
Схема для первой гармоники:
рис.1.3
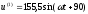
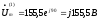
Рассчитаем
значения
и
для первой гармоники:
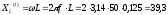
Составим схему с комплексными сопротивлениями:
рис.1.4
На рис.1.4:
Найдём
(параллельное
соединение
и
):
Найдём
:
Находим комплексные значения амплитуд токов:
-
Вторая гармоника:
Схема для второй гармоники:
рис.1.5
Рассчитаем
значения
и
для
второй гармоники:
Составим схему с комплексными сопротивлениями:
рис.1.6
На рис.1.6:
Найдём
(параллельное
соединение
и
):
Найдём
:
Находим комплексные значения амплитуд токов:
Для построения графиков токов переведём градусы в радианы:
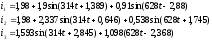
Приложение
Задача №1
Для
проверки расчетных данных используем
результат моделирования схемы в программе
EWB (рис.1.7; рис.1.8):
рис.1.7
рис.1.8
Задача№2.
Расчет трехфазной цепи.
Задание
Рассчитать все токи, определить мгновенное значение напряжения между точками a и b, построить топографическую векторную диаграмму напряжений, совмещенную с лучевой векторной диаграммой токов, рассчитать активную мощность трехфазной цепи.
рис.2.1
;
;
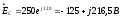
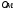
Решение.
2.1. Расчет симметричной трехфазной цепи производится на одну фазу. Расчет произведём по фазе А.
Преобразуем
треугольник сопротивлений (
)
в эквивалентную звезду (
).
(рис.2.2)
рис.2.2
Найдём эквивалентное сопротивление фазы:
Определим линейные токи:
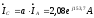
Потеря напряжений в линейных проводах:
Фазное
напряжение на
:
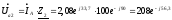В
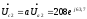В
В
Фазное
напряжение на
:
Фазное
напряжение приёмника
:
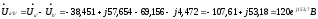
Фазные
токи приёмника
:
Линейное
:
Мгновенное
значение
:
Для проверки расчетных данных (Задача №2) используем результат моделирования схемы в программе EWB(рис 2.3):
Построение
векторной диаграммы для симметричной
трехфазной цепи.(рис 2.4)
рис. 2.4
Задача №3
1. Для исходной схемы цепи рассчитать классическим методом токи i1(t) и i2(t) после поочередного включения рубильников.
2. Построить график зависимости i1(t), учитывающий все коммутации.
3. Используя программу EWB, смоделировать заданные цепи и переходные процессы в них.
Указания
-
Рубильники включаются последовательно в соответствии с указанными на схеме номерами через τ секунд.
При возникновении колебательного процесса τ =Т0/8,
где Т0 – период собственных колебаний.
При возникновении апериодического процесса τ =1/Р1,
где Р1 – корень характеристического уравнения причем [P1]<[P2].
-
Для всех вариантов Е=100 В (источник постоянной ЭДС),
L=125 мГн.
рис.3.1
Параметры цепи:
Решение:
I коммутация:
1)Определяем независимые начальные условия (ННУ), т.е. анализируем схему для момента времени t(0-) (рис.3.2):
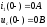
2) Определяем зависимые начальные условия (ЗНУ) в цепи для момента времени t(0+)(рис. 3.3), используя независимые начальные условия и законы Кирхгофа:
Определяем ЗНУ:
3) Определяем принужденную составляющую в момент времени t = ∞ (рис.3.4):
4) Составляем характеристическое уравнение цепи (рис.3.5), определяем его корни:
Переходный
процесс имеет колебательный характер.
5)Определяем постоянные интегрирования. Вычисляем i1(t).
Определяем uc(t):
Длительность переходного процесса:
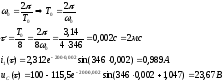
II коммутация:
1) Определяем ННУ t(0-):
2) Определяем ЗНУ в цепи для момента времени t(0+)(рис. 3.6.):
3) Определяем принужденную составляющую в момент времени t = ∞ (рис.3.7):
4) Составляем характеристическое уравнение цепи (рис.3.8), определяем его корни:
Переходный
процесс имеет апериодический характер.
5)Определяем постоянные интегрирования. Вычисляем i1(t).
Длительность переходного процесса:
III коммутация:
1) Определяем ННУ t(0-):
2) Определяем ЗНУ в цепи для момента времени t(0+)(рис. 3.9):
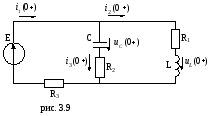
3) Определяем принужденную составляющую в момент времени t = ∞ (рис.3.10):
4) Составляем характеристическое уравнение цепи (рис.3.11), определяем его корни:
