2 семестр / Формулы - 1999 / Formulas

1 а). Вывод формулы полной производной для z=f(x,y), где x=x(t), y=y(t).

Пусть функция z=f(x,y) дифференцируема по переменным (x;y), функции x=x(t), y=y(t) дифференцируемы по t. Тогда сложная функция z=F(t) дифференцируема по t, причем имеет место формула

Док-во:

Из условия дифференцируемости функции z=f(x;y) получаем, что

1 б) Формула Стокса (без доказательства)

Пусть () - гладкая ориентируемая поверхность в R³, которая ограничена замкнутым ориентируемым контуром (). Пусть задано векторное поле, определенное функцией , где функции P,Q,R и их частные производные непрерывны в ()(). Тогда имеет место формула

где - внешняя нормаль к поверхности ().

Или в векторной форме:

Формула из Пискунова:

2 a). Определение полного дифференциала функции двух переменных. Теорема об инвариантности формы полного дифференциала.

Полным дифференциалом дифференцируемой функции будем называть главную линейную часть полного приращения этой функции:

Если (x;y) - независимые переменные, то

Пусть функция z=f(x;y) дифференцируема по (x;y), а функции x=x(u;v), y=y(u;v) дифференцируемы по (u;v). Тогда форма полного дифференциала сохраняется, т.е. она не зависит от того, является ли (x;y) функциями или независимыми переменными.

Док-во:

1) если (x;y) - независимые переменные, то (т.к. z=f(x;y) дифференцируема по (x;y) )

2) Т.к. x=x(u;v); y=y(u;v) дифференцируемы по (u;v) (по условию) и (u;v) - независимые переменные, то

дифференцируема по (u,v) по св-ву сложной функции, значит существует дифференциал. По правилу дифференцирования сложной функции:

2 б) Формула Гаусса-Остроградского (без доказательства)

Пусть в R³ задано некоторое тело (T), которое ограничено гладкой замкнутой ориентируемой поверхностью (), на которой определено поле внешних нормалей ; пусть на (T) задано векторное поле ; функции P,Q,R непрерывны в (T) и на (); кроме того, непрерывны в (T) и на (). Тогда имеет место формула

В векторной форме:

Поток векторного поля через данную поверхность равен тройному интегралу от дивергенции данного векторного поля по телу, ограниченному данной поверхностью.

Формулировка из Пискунова:

3 a). Вывод формулы для производной функции, заданной неявно уравнением f(x,y)=0 с использованием частных производных.

Пусть функция y=y(x) задана неявно уравнением F(x,y)=0. Требуем, чтобы F(x,y) была дифференцируема в т. P(G)R², и в т. P. Тогда в этой точке существует производная y'(x), которая находится по формуле:

Док-во:

Т.к. F(x,y) дифференцируема в т. P(G)R², то

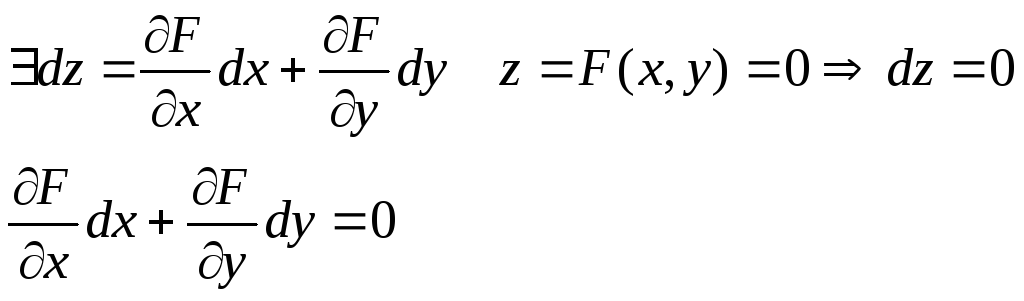
x здесь является независимой переменной, y- функцией. Но по св-ву инвариантности полный дифференциал имеет один и тот же вид, независимо от того, является ли y независимой переменной или функцией других независимых переменных.

3 б) Ротор (определение)

Вектор , определяемый проекциями

называется вихрем или ротором векторной функции и обозначается символом .

В символическом виде:

4 а) Теорема о необходимых и достаточных условиях того, что выражение P(x,y)dx + Q(x,y)dy есть полный дифференциал (доказать необходимость).

Для того, чтобы выражение P(x,y)dx + Q(x,y)dy было полным дифференциалом некоторой функции u=u(x,y), необходимо и достаточно, чтобы при условии, что P(x,y),Q(x,y), непрерывны в некоторой ограниченной односвязной области GR².

Дано: P(x,y)dx + Q(x,y)dy - полный дифференциал.

Док-ть:

Док-во:

Т. к. выражение P(x,y)dx + Q(x,y)dy - полный дифференциал, то по определению

Т. к. P(x,y),Q(x,y), непрерывны в G, то применяем теорему о равенстве вторых смешанных производных:

4 б) Поток вектора через поверхность (определение).

Пусть рассматривается некоторая гладкая ориентируемая поверхность (); пусть в каждой точке M(x;y;z)() задано поле нормалей и задано векторное поле . Поток векторного поля через поверхность () будет определяться поверхностным интегралом

Формулировка из Пискунова:

Поверхностный интеграл называется потоком векторного поля через поверхность .

5 а) Теорема о необходимых и достаточных условиях того, что выражение P(x,y)dx + Q(x,y)dy есть полный дифференциал (доказать достаточность).

Для того, чтобы выражение P(x,y)dx + Q(x,y)dy было полным дифференциалом некоторой функции u=u(x,y), необходимо и достаточно, чтобы при условии, что P(x,y),Q(x,y), непрерывны в некоторой ограниченной односвязной области GR².

Дано:

Док-ть:

Док-во: Для того, чтобы доказать требуемое нужно, чтобы

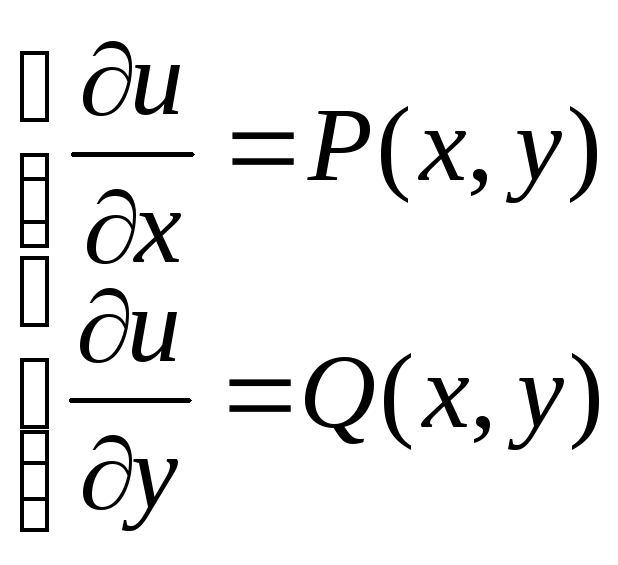
Фиксируем у, интегрируем по x:

5 б) Дивергенция (определение)

Дивергенцией вектора (или дивергенцией векторной функции) называется выражение

6 а). Определение производной по направлению, вывод формулы для ее вычисления.

Производной функции U=u(x,y,z) в т. M₀(x₀,y₀,z₀) по направлению l называется конечный предел (если он существует) отношения приращения функции по данному направлению к смещению, при условии, что смещение стремится к нулю.

Пусть функция U=u(x,y,z) в некоторой окрестности точки M₀(x₀,y₀,z₀) имеет непрерывные частные производные . Пусть вектор

определяет направление l. Тогда

Д-во:

Направление (l) задано вектором .

Тогда M(x,y,z)R³ составляем параметрическое уравнение прямой: x=x₀+tcos, y=y₀+tcos, z=z₀+tcos. Смещение

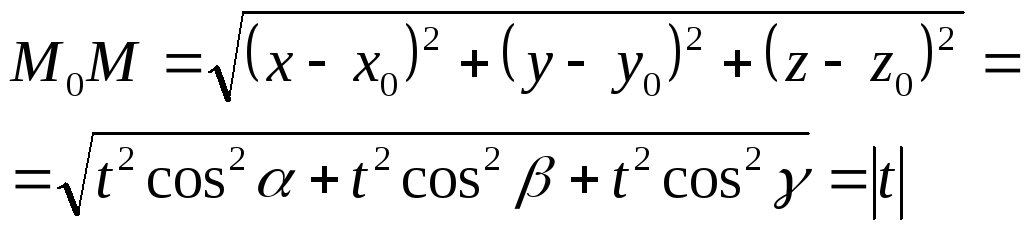
Рассмотрим _lU=U(x,y,z)-U(x₀,y₀,z₀)=

=U(x₀+tcos, y₀+tcos, z₀+tcos)-U(x₀,y₀,z₀) - это сложная функция от t. Введем (t)= U(x₀+tcos, y₀+tcos, z₀+tcos).

Тогда _lU=(t)-(0).

По определению производной по направлению

С другой стороны, U(M)=U(x,y,z)=

=U(x₀+tcos, y₀+tcos, z₀+tcos)=(t).

По правилу дифференцирования сложной функции

6 б). Вычисление массы и объема тела через тройной интеграл

7а) Определение градиента скалярного поля, доказать его свойства.

Градиентом скалярного поля в точке M(x,y,z) будем называть вектор, проекции которого на координатные оси равны значениям частных производных в этой точке.

Свойства градиента:

 Связь градиента и производной по направлению

Пусть функция U=u(x,y,z) дифференцируема в некоторой области GR³. Пусть в точке M(x,y,z)G. Рассмотрим некоторое направление (l): . Тогда

Док-во:

Отсюда следует, что значение производной по направлению равно проекции градиента на это направление:

 Производная по направлению имеет наибольшее значение, если это направление совпадает с направлением градиента.

При этом

Док-во:

 Производная по направлению, перпендикулярному направлению градиента, равна 0.

Док-во:

 В каждой точке поверхности уровня скалярного поля u(x,y,z)=C градиент направлен по нормали к этой поверхности в сторону возрастания функции.

Док-во:

В R³ - поверхность уровня U(x,y,z)=C=const

F(x,y,z)=U(x,y,z)-C=0

gradF=gradU.

Следствие:

В R² градиент будет направлен перпендикулярно касательной к линии уровня.

Градиент в каждой точке поверхности уровня характеризует наибольшую скорость изменения скалярного поля.

 U₁=u₁(x,y,z), U₂=u₂(x,y,z)

Тогда grad(U₁+U₂)=gradU₁+gradU₂

 U=u(x,y,z), A=const

Тогда grad(AU)=AgradU

7 б). Свойства двойного интеграла, теорема о среднем.

 Если f(x,y)=1, то

 Постоянный множитель можно выносить за знак двойного интеграла



 Аддитивность. Пусть (G)=(G₁)(G₂), причем (G₁) (G₂)=, то

 Пусть функция z=f(x,y) непрерывна в области (G) и известно, что существуют такие m и M, что mf(x,y)M. Тогда

 Теорема о среднем.

Пусть функция z=f(x,y) непрерывна в ограниченной замкнутой области . Тогда существует точка P(;)(G) такая что:

8 а). Определение максимума (минимума) функции двух переменных. Доказать теорему о необходимых условиях существования экстремума.

Точка M₀ называется точкой локального максимума [локального минимума] функции z=f(x,y), если существует такая >0 - окрестность точки M₀, такая что M(x;y)U_(M₀), MM₀, выполняется неравенство f(M)<f(M₀) [f(M)>f(M₀)].

Пусть функция z=f(x;y) во внутренней точке M₀G имеет локальный экстремум. Тогда если в этой точке существуют частные производные, то они равны 0.

Док-во:

Пусть точка M₀(x₀,y₀)(G) - точка локального максимума для функции z=f(x;y). Тогда

Фиксируем y=y₀. Рассматриваем функцию f(x,y₀)=f₁(x)

функция f₁(x) имеет в точке x₀ локальный максимум. По необходимым условиям экстремума функции f₁(x) .

Фиксируем x=x₀. Рассматриваем функцию f(x₀,y)=f₂(y)

функция f₂(y) имеет в точке y₀ локальный максимум. По необходимым условиям экстремума функции f₂(y) .

Аналогичное док-во, если M₀(x₀,y₀) - точка локального минимума.

8 б). Вычисление площади области через двойной и криволинейный интегралы.

9 а). Двойной интеграл: определение, свойства, вычисление в декартовой системе координат.

Двойным интегралом от функции z=f(x,y) по области (G) называется конечный предел, если он существует, таких интегральных сумм причем этот предел не зависит ни от способа разбиения области на элементарные части, ни от выбора точек P_k(_k,_k)

Свойства:

 Если f(x,y)=1, то

 Постоянный множитель можно выносить за знак двойного интеграла



 Аддитивность. Пусть (G)=(G₁)(G₂), причем (G₁) (G₂)=, то

 Пусть функция z=f(x,y) непрерывна в области (G) и известно, что существуют такие m и M, что mf(x,y)M. Тогда

 Теорема о среднем.

Пусть функция z=f(x,y) непрерывна в ограниченной замкнутой области . Тогда существует точка P(;)(G) такая что:

Пусть функция z=f(x,y) непрерывна в области (G), правильной относительно oy:

Пусть существует . Кроме того, . Тогда , причем

9 б). Формулировка достаточных условий существования экстремума функции двух переменных.

Пусть функция z=f(x,y) определена и непрерывна вместе со своими частными производными второго порядка в U_(M₀), >0, т. M₀ - стационарная точка. Обозначим:

Тогда:

1. Если , то экстремум есть,

причем, если A>0 (или C>0), то локальный минимум, если A<0 (или C<0), то локальный максимум.

2. Если (M₀)<0, то экстремума нет.

3. Если (M₀)=0, то требуются дополнительные

исследования.

10 а). Двойной интеграл: определение, свойства, вычисление в полярной системе координат.

Двойным интегралом от функции z=f(x,y) по области (G) называется конечный предел, если он существует, таких интегральных сумм причем этот предел не зависит ни от способа разбиения области на элементарные части, ни от выбора точек P_k(_k,_k)

Свойства:

 Если f(x,y)=1, то

 Постоянный множитель можно выносить за знак двойного интеграла



 Аддитивность. Пусть (G)=(G₁)(G₂), причем (G₁) (G₂)=, то

 Пусть функция z=f(x,y) непрерывна в области (G) и известно, что существуют такие m и M, что mf(x,y)M. Тогда

 Теорема о среднем.

Пусть функция z=f(x,y) непрерывна в ограниченной замкнутой области . Тогда существует точка P(;)(G) такая что:

10 б). Определение частных производных, их геометрический смысл.

Частной производной по x функции z=f(x,y) называется конечный предел (если он существует) отношения частного приращения по x к x при условии, что x0.

Геометрический смысл:

Значение частной производной по x в некоторой точке равно тангенсу угла наклона касательной, проведенной к сечению данной поверхности z=f(x,y) плоскостью y=y₀.

11 а). Криволинейный интеграл по координатам: определение, свойства, вычисление. Работа силы.

Криволинейным интегралом II рода (криволинейным интегралом по координатам) от функций P(x,y), Q(x,y) по кривой AB называется конечный предел, если он существует, таких сумм:

, который не зависит ни от способа разбиения дуги AB на элементарные дуги, ни от выбора точек N_k(_k,_k) на каждой элементарной дуге.

Свойства:

1. Криволинейный интеграл II рода обладает всеми основными свойствами определенного интеграла:

-постоянный множитель можно вынести за знак интеграла;

-интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от каждого из слагаемых.

-криволинейный интеграл по кривой, состоящей из одной точки, равен 0.

2. Криволинейный интеграл меняет знак при изменении ориентации кривой, т. е.

3. Если (AB)=(AC)(CB), то

Вычисление:

Пусть кривая (AB), по которой ведется интегрирование, задана параметрически: ; функции x(t), y(t) непрерывно дифференцируемы на [,]; а функции P(x,y)=P(x(t),y(t)), Q(x,y)=Q(x(t),y(t)) как функции t непрерывны на этом отрезке. Тогда

Если кривая (AB) задана в явном виде: y=f(x), x[a;b]. Тогда если y=f(x) непрерывно дифференцируема на [a;b], то

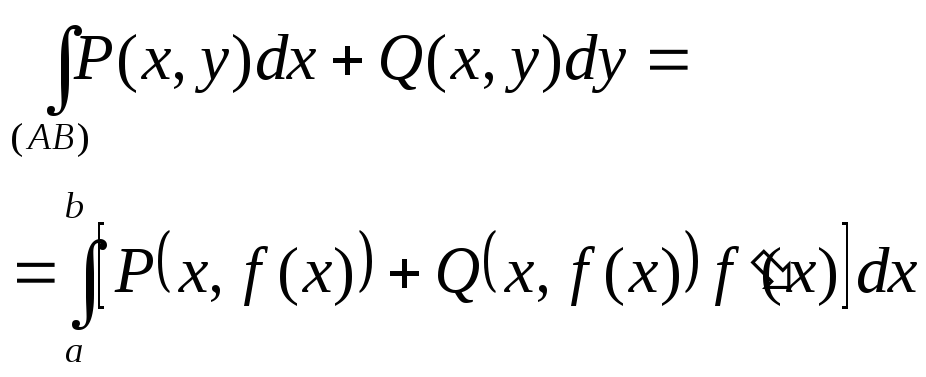
Работа силы:

Пусть в R² задано силовое поле, которое определяется вектором силы . Тогда

численно равен работе силы по перемещению материальной точки единичной массы из точки A в точку B по кривой AB.

11 б). Теорема о равенстве двух смешанных производных второго порядка.

Пусть функция z=f(x,y) определена в (G)R², и существуют непрерывные вторые смешанные частные производные . Тогда эти смешанные производные равны.

12 а). Интеграл Эйлера-Пуассона.

Интегралом Эйлера-Пуассона называется несобственный интеграл вида

Теорема:

Док-во:

12 б). Формулы для производной сложной функции нескольких переменных (случай 2-х от 3-х переменных или 3-х от 2-х переменных).

z=f(x,y), x=x(u,v,w), y=y(u,v,w) (z дифференцируема по (x,y); x,y дифференцируемы по (u,v,w) ).

w=f(x,y,z), x=x(u,v), y=y(u,v), z=z(u,v) (w дифференцируема по (x,y,z); x,y,z дифференцируемы по (u,v) ).

13 а). Криволинейный интеграл: определение, свойства. Доказать теорему о независимости криволинейного интеграла от пути интегрирования.

Криволинейным интегралом II рода (криволинейным интегралом по координатам) от функций P(x,y), Q(x,y) по кривой AB называется конечный предел, если он существует, таких сумм:

, который не зависит ни от способа разбиения дуги AB на элементарные дуги, ни от выбора точек N_k(_k,_k) на каждой элементарной дуге.

Свойства:

1. Криволинейный интеграл II рода обладает всеми основными свойствами определенного интеграла:

-постоянный множитель можно вынести за знак интеграла;

-интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от каждого из слагаемых.

-криволинейный интеграл по кривой, состоящей из одной точки, равен 0.

2. Криволинейный интеграл меняет знак при изменении ориентации кривой, т. е.

3. Если (AB)=(AC)(CB), то

Пусть функции P, Q, непрерывны в односвязной области (G)R². Тогда для того, чтобы не зависел от пути интегрирования, необходимо и достаточно, чтобы .

Док-во:

Достаточность:

Дано:

Док-ть: не зависит от пути интегрирования.

Док-во:

Пусть () - некоторый контур в (G). Тогда

По теореме о равенстве 0 криволинейного интеграла по замкнутому контуру не зависит от пути интегрирования.

Необходимость:

Дано: не зависит от пути интегрирования.

Док-ть:

Док-во:

Из теоремы о равенстве 0 криволинейного интеграла по замкнутому контуру следует, что

В силу непрерывности функций, входящих в это неравенство, существует такая окрестность U_(M₀), >0, что

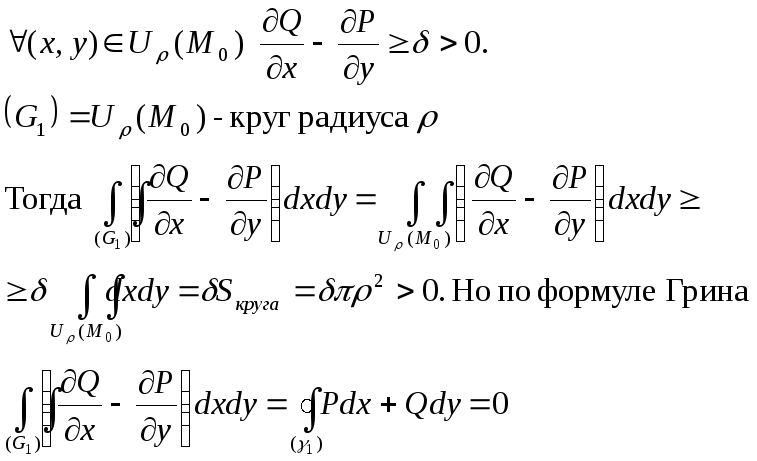
Противоречие. Оно устраняется, если

13 б) Формула Гаусса-Остроградского (без доказательства)

Пусть в R³ задано некоторое тело (T), которое ограничено гладкой замкнутой ориентируемой поверхностью (), на которой определено поле внешних нормалей ; пусть на (T) задано векторное поле ; функции P,Q,R непрерывны в (T) и на (); кроме того, непрерывны в (T) и на (). Тогда имеет место формула

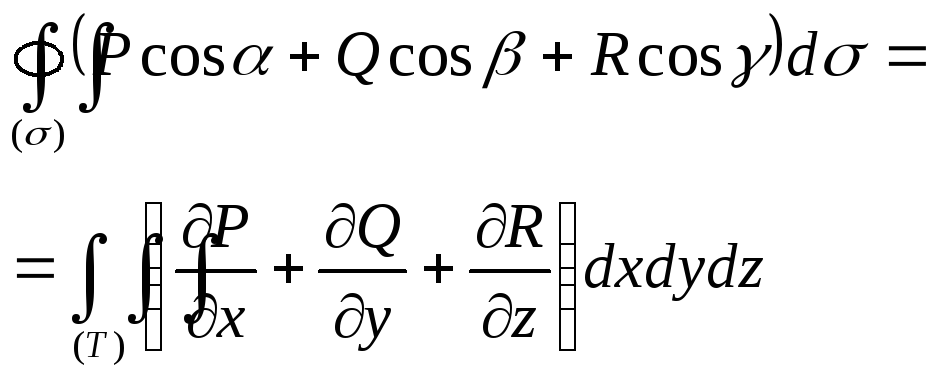
В векторной форме:

Поток векторного поля через данную поверхность равен тройному интегралу от дивергенции данного векторного поля по телу, ограниченному данной поверхностью.

14 а). Доказать формулу Грина.

Пусть в R² задана замкнутая кривая (), ограничивающая некоторую область (G), причем эта область является правильной как относительно оси оy, так и относительно оси ox. Пусть функции P(x,y),Q(x,y), непрерывны в замкнутой области , причем контур () обходится против часовой стрелки. Тогда

Док-во:

1 часть:

(G) - правильная относительно оси oy:

2 часть:

(G) - правильная относительно ox:

Складывая выражения, полученные в 1-ой и 2-ой частях, получаем:

14 б). Потенциальное поле, потенциальная функция. Выражение криволинейного интеграла через потенциальную функцию (и наоборот).

Векторное поле в R², определяемое функцией , называется потенциальным, если существует такая скалярная функция u=u(x,y), для которой . Такая функция u называется потенциальной функцией (или потенциалом) данного векторного поля .