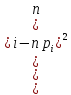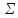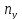- •Математическая обработка статистических данных
- •Содержание
- •Введение
- •Индивидуальные задания
- •Вариант №1
- •Вспомогательная таблица для расчета числовых характеристик выборки
- •Расчетная таблица для вычисления
- •Корреляционная таблица эмпирического распределения двумерной случайной величины (X, y)
- •Заключение
- •Список использованной литературы
Расчетная таблица для вычисления
|
Интервалы
|
Частоты эмпирические ni |
Вероятности pi |
Теоретические частоты npi |
|
|
|
2 |
0,02442 |
2,442 |
0,08 |
|
|
6 |
0,06258 |
6,258 |
0,0106 |
|
|
17 |
0,13663 |
13,663 |
0,815 |
|
|
19 |
0,21281 |
21,281 |
0,2445 |
|
|
21 |
0,2372 |
23,72 |
0,3119 |
|
|
20 |
0,1795 |
17,95 |
0,2341 |
|
|
11 |
0,09739 |
9,739 |
0,1633 |
|
|
3 |
0,03756 |
3,756 |
0,1522 |
|
|
1 |
0,01191 |
1,191 |
0,0306 |
|
|
100 |
1 |
100 |
2,0422 |
Значение
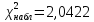 .
.
В
таблице критических точек распределения
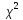 по уровню значимости
по уровню значимости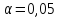 и числу степеней свободы
и числу степеней свободы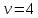 найдем критическое значение
найдем критическое значение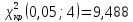 .
.
Так
как
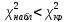 ,
то считаем, что нет оснований для
отклонения нулевой гипотезы при заданном
уровне значимости
,
то считаем, что нет оснований для
отклонения нулевой гипотезы при заданном
уровне значимости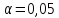 .
.
Построим
график эмпирической функции
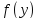 .
Для этого из середины частичных интервалов
восстановим перпендикуляры высотой
равнойpi
– вероятностям попадания СВ Y
в соответствующий частичный интервал.
На рис.3 концы перпендикуляров отмечены
точками, полученные точки соединены
плавной кривой.
.
Для этого из середины частичных интервалов
восстановим перпендикуляры высотой
равнойpi
– вероятностям попадания СВ Y
в соответствующий частичный интервал.
На рис.3 концы перпендикуляров отмечены
точками, полученные точки соединены
плавной кривой.
РИС. 3
Сравнение
полигона относительных частот и
нормальной кривой показывает, что
построенная нормальна кривая
удовлетворительно сглаживает полигон.
Найдем
интервальные оценки параметров
нормального закона распределения. Для
нахождения доверительного интервала,
покрывающего математическое ожидание
СВ У, найдем по таблицам квантилей
распределения Стьюдента по заданной
доверительной вероятности 0,95 и числу
степеней свободы
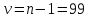 число
число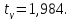
Вычислим предельную погрешность интервального оценивания:
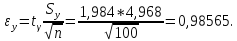
Запишем искомый доверительный интервал для мат. ожидания a:
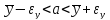
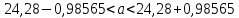
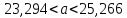
Если будет произведено достаточное большое число выборок из одной и той же генеральной совокупности, что в 95% выборок доверительный интервал (23,294;25,266) покроет математическое ожидание a; и только в 5% выборок математическое ожидание может выйти за границы доверительного интервала.
Для
нахождения доверительного интервала,
покрывающего неизвестное среднее
квадратическое отклонение
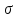 с заданной вероятностью
с заданной вероятностью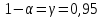 ,
найдем по
,
найдем по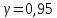 и числу степеней свободы
и числу степеней свободы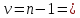
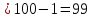 два
числа
два
числа
 и
и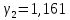 .
.
Искомый доверительный интервал равен:
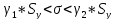
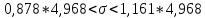
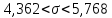
Если
будет произведено достаточно большое
число выборок из одной и той же генеральной
совокупности, что в 95% выборок доверительный
интервал (4,362;5,768) покроет среднее
квадратическое отклонение
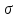 ,
и только в 5% среднее квадратическое
отклонение
,
и только в 5% среднее квадратическое
отклонение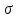 может выйти за границы доверительного
интервала (4,362;5,768).
может выйти за границы доверительного
интервала (4,362;5,768).
Проведем корреляционный анализ выборочных данных СВ X и СВ Y.
Составим корреляционную таблицу. Интервалы для СВX:
(10,1;19,9], (19,9;29,7], (29,7;39,5], (39,5;49,3], (49,3;59,1], (59,1;68,9], (68,9;78,7], (78,7;88,5], (88,5;98,3].
Интервалы для СВ Y:
(11,5;14,5], (14,5;17,5], (17,5;20,5], (20,5;23,5], (23,5;26,5], (26,5:29,5], (29,5;32,5], (32,5;35,5], (35,5;38,5].
ТАБЛИЦА 4
Корреляционная таблица эмпирического распределения двумерной случайной величины (X, y)
|
|
15 |
24,8 |
34,6 |
44,4 |
54,2 |
64 |
73,8 |
83,5 |
93,4 |
|
|
13 |
1 |
1 |
|
|
|
|
|
|
|
2 |
|
16 |
2 |
3 |
1 |
|
|
|
|
|
|
6 |
|
19 |
1 |
4 |
5 |
5 |
2 |
|
|
|
|
17 |
|
22 |
|
1 |
9 |
8 |
1 |
|
|
|
|
19 |
|
25 |
|
|
1 |
7 |
6 |
7 |
|
|
|
21 |
|
28 |
|
|
|
1 |
6 |
6 |
7 |
|
|
20 |
|
31 |
|
|
|
|
1 |
3 |
4 |
3 |
|
11 |
|
34 |
|
|
|
|
|
1 |
1 |
1 |
|
3 |
|
37 |
|
|
|
|
|
|
|
|
1 |
1 |
|
|
4 |
9 |
16 |
21 |
16 |
17 |
12 |
4 |
1 |
100 |
Зная,
что
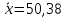 ,
, ,
,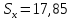 ,
,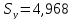 ,
вычисляем сначала выборочный корреляционный
момент:
,
вычисляем сначала выборочный корреляционный
момент:
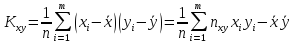
где m – число заполненных клеток.
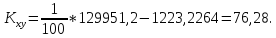
Выборочный коэффициент корреляции:
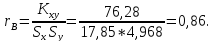
Положительный знак выборочного коэффициента корреляции rB показывает, что с увеличением значений СВ Х эмпирические значения СВ У в среднем увеличиваются.
Проверим
значимость полученного выборочного
коэффициента корреляции, то есть проверим
нулевую гипотезу о том, что коэффициент
корреляции p
равен нулю
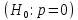 при альтернативной гипотезе
при альтернативной гипотезе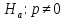 .
.
Вычислим
статистику:
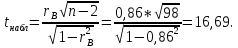
Принятие
гипотезы Ha
при уровне значимости
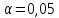 означает, что выборочный коэффициент
корреляции отличается от нуля с ошибкой
5%.
означает, что выборочный коэффициент
корреляции отличается от нуля с ошибкой
5%.
Коэффициент Стьюдента равен 1,984.
Так
как
 ,
то нулевая гипотеза отвергается и
коэффициент корреляции можно считать
существенным, а связь между СВ достоверной,
то есть
,
то нулевая гипотеза отвергается и
коэффициент корреляции можно считать
существенным, а связь между СВ достоверной,
то есть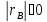 .
Поэтому между СВ Х и СВ У существует
корреляционная зависимость.
.
Поэтому между СВ Х и СВ У существует
корреляционная зависимость.
Построим
корреляционное поле. Изобразим результаты
измерений
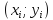 в виде точек в декартовой системе
координат.
в виде точек в декартовой системе
координат.
РИС. 4 – Корреляционное поле и линии регрессии
Найдем
выборочное уравнение регрессии Y
на X:
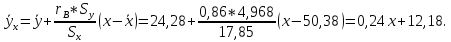
Найдем выборочное уравнение регрессии X на Y:
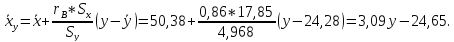
Контроль вычислений:
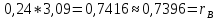
Графики найденных выборочных функций регрессии нанесены на рис.4
ВЫВОД
Была проведена исследовательская работа над случайной двумерной величиной Х – кол-во обработанных деталей, шт.; У – время непрерывной работы станков, ч. Были построены интервальный и дискретный статистически ряды распределения частот и относительных частот, гистограммы и полигоны относительных частот, эмпирические функции распределения. Были вычислены числовые характеристики выборки: выборочная средняя, выборочная дисперсия, выборочные коэффициенты асимметрии и эксцесса. Для Х – кол-во обработанных деталей и для У – время непрерывной работы станков, ч. несимметричный полигон (гистограмма) Правосторонняя асимметрия данного распределения, и полигон менее крут чем нормальная кривая.
Х – кол-во обработанных деталей, шт.; У – время непрерывной работы станков, ч. распределены по нормальному закону, это видно исходя из механизма их образования, по виду гистограммы и полигона относительных частот и по значениям выборочных коэффициентов асимметрии и эксцесса.
Далее были найдены точечные оценки параметров нормального закона распределения, и записаны функции плотности распределения вероятностей для Х – кол-во обработанных деталей, шт.; и для У – время непрерывной работы станков, ч.
Проверил с помощью критерия согласия Пирсона гипотезу о том, что выборка извлечена из генеральной совокупности с предполагаемым нормальным законом распределения. Была приняты гипотезы и найдены интервальные оценки параметров нормального закона распределения.
И
теперь соединив значения Х – кол-во
обработанных деталей, шт.; У – время
непрерывной работы станков, ч. провел
корреляционный анализ: составил
корреляционную таблицу; нашел выборочный
коэффициент корреляции; проверил
значимость выборочного коэффициента
корреляции rв;
построил корреляционное поле и по
характеру расположения точек на нем
подобрать общий вид функции регрессии;
нашел эмпирические функции регрессии
У – время непрерывной работы станков,
ч. на Х – кол-во обработанных деталей,
шт.;, X на Y и построил их графики.