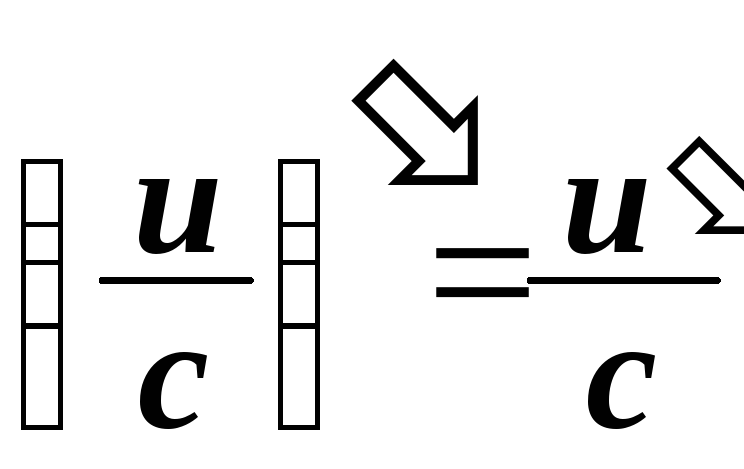- •Ключевые слова
- •Умножение
- •Векторы:
- •Аналитическая геометрия:
- •Прямая и плоскость в пространстве
- •Кривые второго порядка
- •Уравнение нормали:
- •Интегральное исчисление
- •Двойные интегралы:
- •Дифференциальные уравнения (ду)
- •(Распределение Бернулли)
- •Математическая статистика
- •Абстрактная алгебра
- •(Например, ), –шаг.
- •Формулы комбинаторики:
- •V это непустое множество вершин,
- •V это непустое множество вершин или узлов,
- •0 Во всех остальных случаях.
Кривые второго порядка
|
Эллипс |
эксцентриситет
ε =
|
|
|
Окружность |
с центром в начале координат О(0,0), радиусом R:
|
с центром в точке С(х0; у0) и радиусом R:
|
|
Гипербола |
а
эксцентриситет
ε =
а
y |
|
|
П
|
F
х2 = 2ру
x
О
Эксцентриситет ε =1
|
|
Преобразовать уравнение кривой к
каноническому виду – выделить полный
квадрат по каждой переменной
(полный квадрат:
![]() ):
):
 .
.

Уравнение касательной плоскости
к поверхности
![]() в точке
в точке
![]() имеет вид
имеет вид
![]() – (z – z0)
= 0.
– (z – z0)
= 0.
Уравнение касательной плоскости
к поверхности
![]() в т.
в т.
![]() имеет
вид
имеет
вид
![]() .
.
Кривизна K кривой
![]() равна
равна
 ;
для кривой
;
для кривой
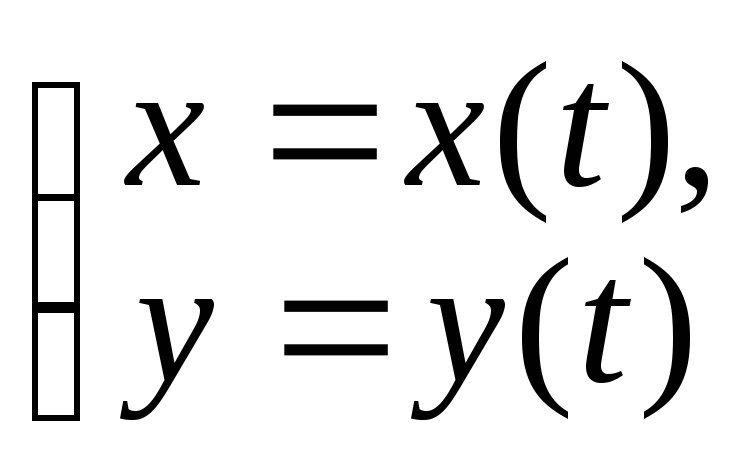
 .
Для прямой линии кривизна
.
Для прямой линии кривизна
![]() ,
для окружности радиуса r
,
для окружности радиуса r
![]() .
Радиус R кривизны
связан с кривизной K
равенством
.
Радиус R кривизны
связан с кривизной K
равенством
![]() .
Центр кривизны имеет координаты
.
Центр кривизны имеет координаты
 .
.
Годограф вектор-функции
![]() –линия
описываемая концом вектора
–линия
описываемая концом вектора
![]() .
Производная вектор-функции
.
Производная вектор-функции
![]() –
вектор, направленный по касательной к
годографу
–
вектор, направленный по касательной к
годографу
Производная и ее приложения
6 |
(sin и) = cos и и (cos u) = – sin и и |
|
Уравнение
касательной:
![]()






 арабола
арабола



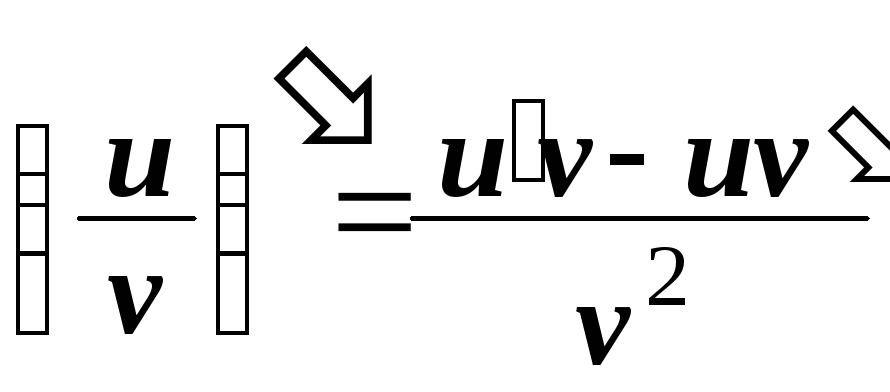
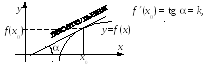 .а.
.а.