27

Ключевые слова

Асимптота 8

Алгебра 18

Бинарное отношение 18

Вектор 4

–собственный 3

Векторное произведение 4

Вероятность 14

Выборка 15

Гармонические колебания 13

Гипербола 6

Гипотеза основная 15

– конкурирующая 15

Годограф 7

Градиент 9

Граф 20

Группа 18

Дифференциальное уравнение 11

Замыкание 3

Замкнутое множество 3

Интеграл 10

–определенный 10

–несобственный 10

Интегральное уравнение 19

Интервал сходимости 12

Интервальная оценка 15

Интерполяционный полином 19

Касательная

–к кривой 8

–плоскость 7

Квадратичная форма 17

Комплексное число 16

Корень уравнения 19

-кратный 17

-многочлена 17

Коэффициент корреляции 15

Кольцо 18

Кривизна 7

Линия уровня 9

Матрица 2

– оператора (отображения) 3

– расширенная 2

Математическое ожидание 14

Мера 3

Множество 3, 18

Мода 15

Норма вектора 4

Окрестность точки 3

Определитель 2

Образ 3

Особая точка 16

Открытое множество 3

Параллельные прямые, плоскости 5

Перестановки 19

Перпендикулярные

–прямые 5

–плоскости 5

Периодические функции 13

Плоскость 5

Поверхность 7

Поле 18

Полярные координаты 9

Прямая 5

Производная 8

Радиус

–кривизны 7

–сходимости 12

Размещения 19

Разложение дробей 17

Расстояние 3,4,5

Регрессии уравнение 15

Рефлексивность 18

Ряд

–степенной 12

–числовой 12

–Фурье 13

Середина отрезка 4

Симметричность 18

Скалярное произведение 4

Случайные события 14

–совместные 14

–независимые 14

Собственные значения 3

Сочетания 19

Сравнение рядов 12

Статистическое распределение 15

Сходимость ряда 12

Таблицы истинности 20

Точечная оценка 15

Транзитивность 18

Угол

–между прямыми 5

– между плоскостями 5

Формула Эйлера 19

Характеристические числа 3

Характеристическое уравнение 3

Число способов выбора 19

Определите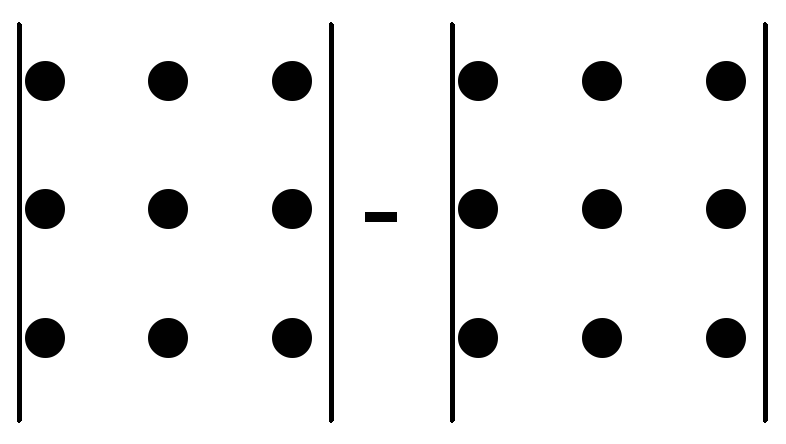ли:,

 или

Алгебраические дополнения элементов матрицы:



 элемента 

элемента 

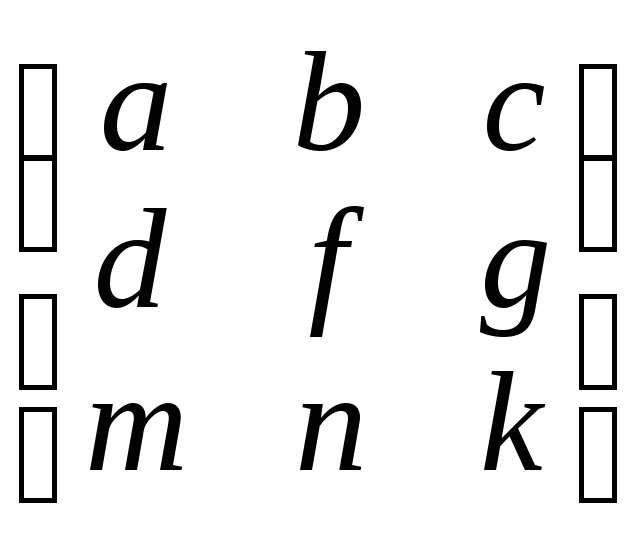
Матрицы: сложение

Умножение

Обратная к , где

Ранг матрицы – число ненулевых строк в матрице, преобразованной к треугольному виду:

(–3)

(–2)

+

(–1)

+

+

 

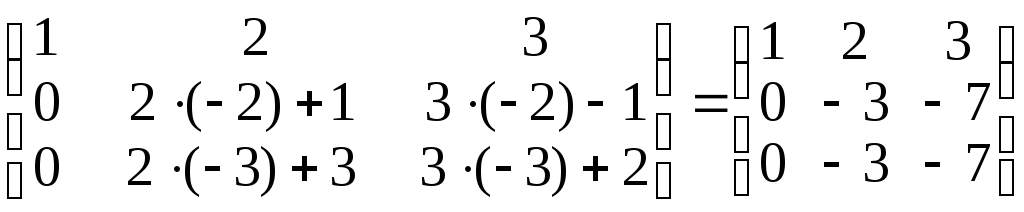
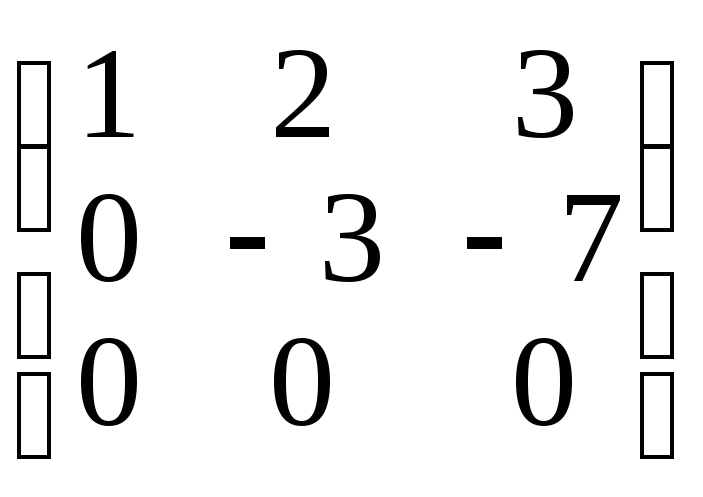
Системы линейных уравнений:

основная матрица системы,

матрица-столбец

неизвестных

матрицу-столбец

свободных членов

расширенная матрица

системы

Х = В =

Правило Крамера , например

, =25,  и т.д.

Линейные преобразования (отображения)

А–матрица преобразования (отображения) A, Х – столбец координат вектора. Образ вектора Х при преобразовании A равен АХ. A – линейное если A(х+у)= Aх+Aу, A(λх)= λ(Aх).

Если =АХ+В–отображение, то образ отрезка равен .

Собственные числа матрицы – корни _1,2 характеристического уравнения

,

Собственные векторы матрицы А – такие векторы и, что Аи = и. Например:

, и= Аи = =20и

Метрические пространства (МП)

Множество М – метрическое пространство, если х,уМ определено число (расстояние между точками) такое, что:

1); 2) , хМ; 3) .

Примеры: R, Rⁿ, множество непрерывных на [a, b] функций, множество интегрируемых с квадратом на [a, b] функций. В R , в Rⁿ _. -Окрестность точки аМП – множество точек х таких, что .

-Окрестность в R – интервал, в R² - круг радиуса  с центром в т.а.

х – предельная точка М, если в  ее окрестности есть другие точки М; х – внутренняя точка М, если  ее окрестность, содержащая только точки М. М – замкнуто, если содержит все свои предельные точки (содержит свою границу); М – открыто, если все его точки – внутренние (не содержит граничных точек). М – полное, если в нем всякая фундаментальная последовательность сходится. Примеры полных МП; Rⁿ, . Замыкание множества М – это множество{М{все предельные точки М (или граничные)}}

Компакт–замкнутое, ограниченное множество.

Множество А–замкнуто в М, если М\A– открыто.