
Задача №3 Экономический анализ производственной функции
Цель работы: Получение линейной производственной функции средствамиExcelи ее экономический анализ.
Задание:
Приведена выборка пятнадцати значений выпуска продукции Y, затрат основных производственных фондов K и ресурсов трудозатрат L.
Требуется:
построить производственную функцию в форме линейной зависимости
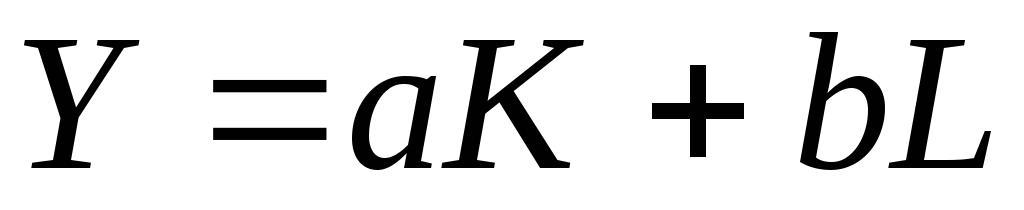 ;
;провести имитационные расчеты трех вариантов планов производства продукции при следующих предположениях:
а) выбрать значения
выпуска продукции базового периода
![]() и трудозатрат
и трудозатрат![]() близкие к исходным данным;
близкие к исходным данным;
б) выпуск в следующем периоде увеличить на 25%;
в) далее еще на
25%, предполагая, что затраты ресурса
![]() не ограничены, а трудозатраты должны
оставаться на прежнем уровне;
не ограничены, а трудозатраты должны
оставаться на прежнем уровне;
определить средние эффективности производственных ресурсов
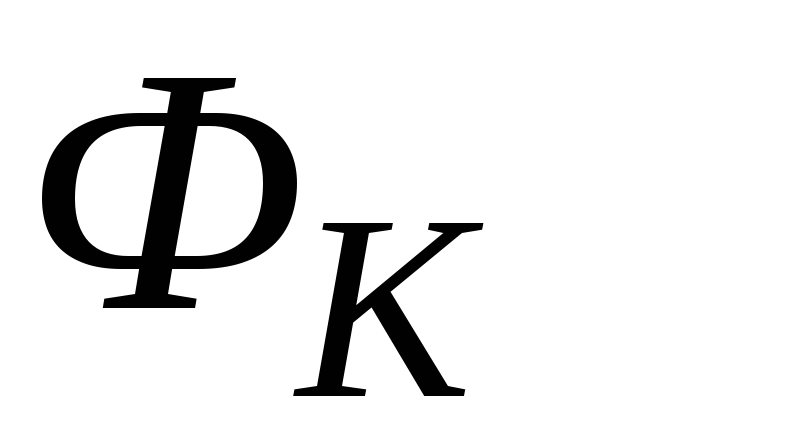 и
и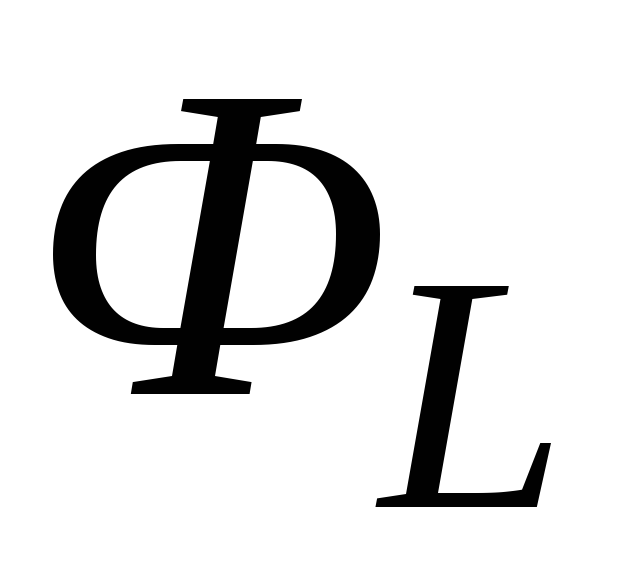 для трех вариантов планов, дать
экономический анализ найденным числовым
характеристикам;
для трех вариантов планов, дать
экономический анализ найденным числовым
характеристикам;рассчитать для трех вариантов предельные эффективности ресурсов
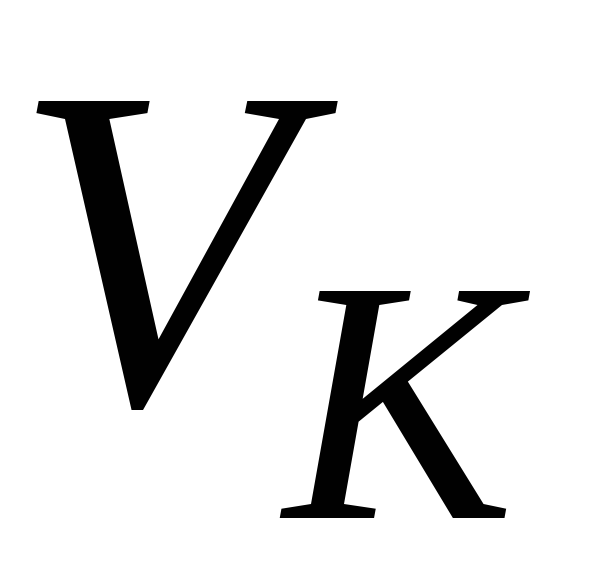 и
и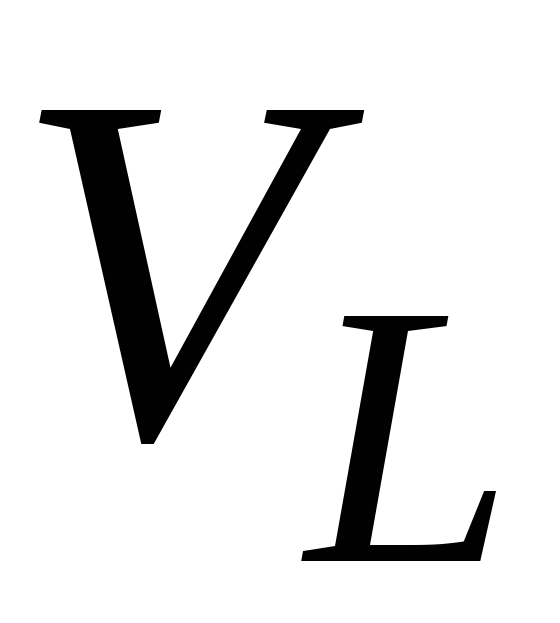 ,
проанализировать результаты;
,
проанализировать результаты;найти коэффициенты эластичности выпуска по ресурсам

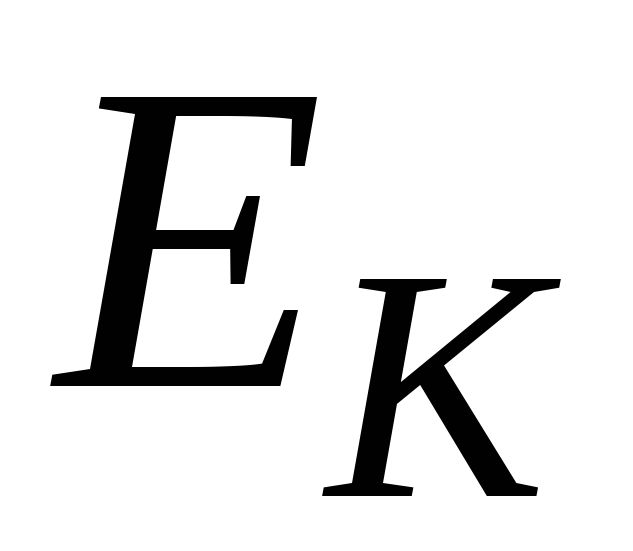 и
и
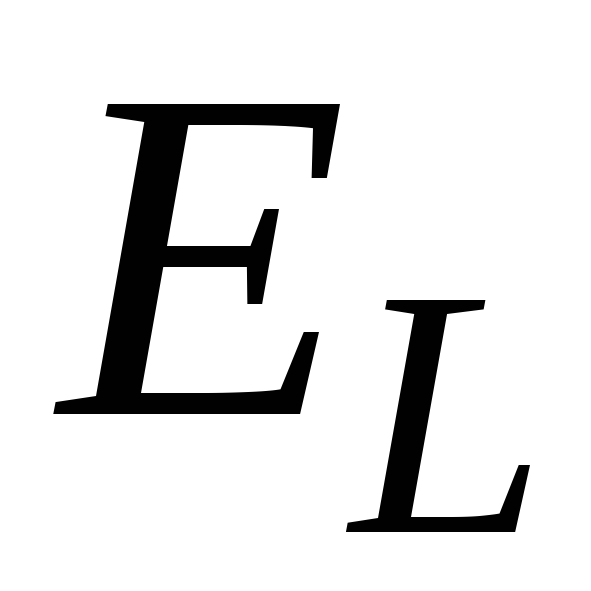 ,
вычислить и проанализировать результаты
при заданных значениях выпуска и
факторов;
,
вычислить и проанализировать результаты
при заданных значениях выпуска и
факторов;определить предельные нормы замещения ресурсов, дать экономический анализ полученным числовым характеристикам;
построить изокванты модели при фиксированных значениях выпуска, которые следует выбрать самостоятельно.
Таблица 3.1 – Исходные данные
|
№4 |
1 |
2 |
3 |
|
1 |
15,16 |
32,1 |
24,56 |
|
2 |
16,7 |
31 |
23,7 |
|
3 |
15,44 |
32,4 |
23,78 |
|
4 |
15,65 |
33,2 |
24,1 |
|
5 |
13,13 |
31,2 |
24 |
|
6 |
14,22 |
34,8 |
23,67 |
|
7 |
16,73 |
35,4 |
24,9 |
|
8 |
17,8 |
33 |
32,75 |
|
9 |
16,88 |
34,8 |
26,24 |
|
10 |
15,67 |
33,3 |
25,37 |
|
11 |
15,99 |
36,1 |
25,66 |
|
12 |
14,33 |
38,3 |
24,34 |
|
13 |
15,77 |
30,6 |
22,1 |
|
14 |
15,28 |
32,1 |
20,57 |
|
15 |
17,04 |
37,6 |
24,61 |
Решение.
Построим производственную функцию в форме линейной зависимости
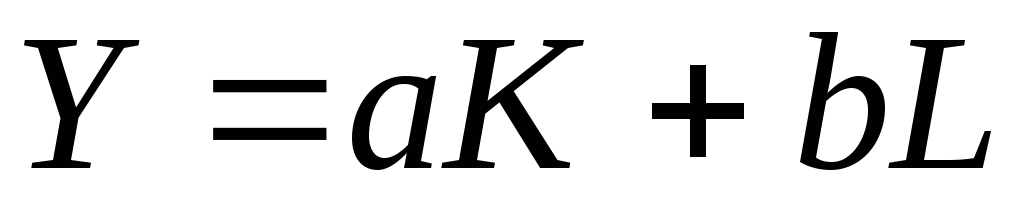 .
.
Таблица 3.2 - Расчеты вариантов планов
|
|
| ||||
|
Параметры производственной функции |
| ||||
|
| |||||
|
| |||||
|
| |||||
|
B |
|
A |
| ||
|
|
|
|
| ||
|
0,34 |
|
0,21 |
| ||
Таким образом производственная линейная функция имеет вид:
![]() ,
(1)
,
(1)
где
![]() -
это затраты основных производственных
фондов (ОПФ),
-
это затраты основных производственных
фондов (ОПФ),
а
![]() -ресурсы
трудозатрат.
-ресурсы
трудозатрат.
2. Проведем имитационные расчеты трех вариантов планов производства продукции при следующих предположениях:
Выберем значения
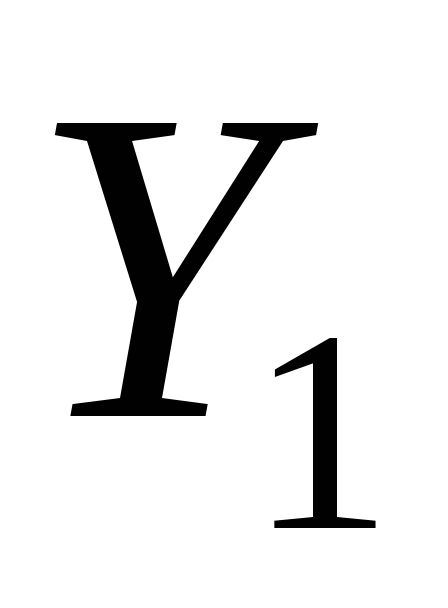 и
и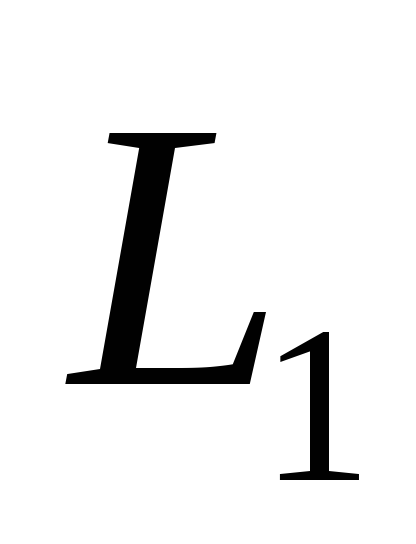 близкие к исходным данным. Пусть в
базовом периоде выпускалось 16 ед. (одна
единица, например, соответствует 100 000
руб.) продукции, т.е.
близкие к исходным данным. Пусть в
базовом периоде выпускалось 16 ед. (одна
единица, например, соответствует 100 000
руб.) продукции, т.е.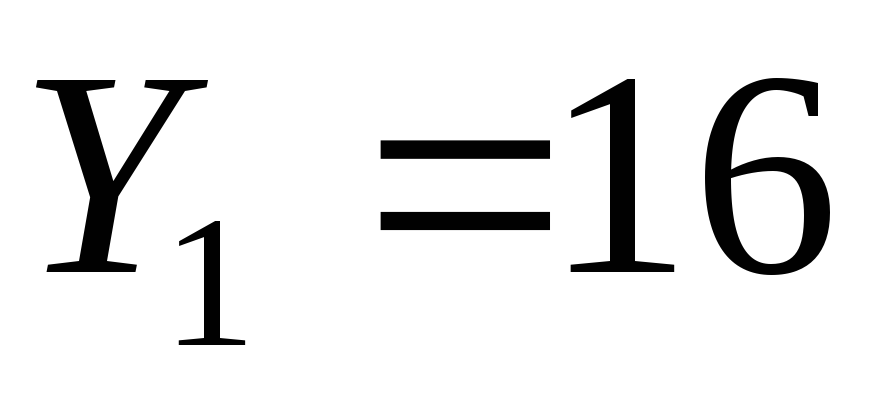 .
Предположим, что на этот объем выпуска
продукции расходовалось 33 единицы
трудозатрат, т.е.
.
Предположим, что на этот объем выпуска
продукции расходовалось 33 единицы
трудозатрат, т.е.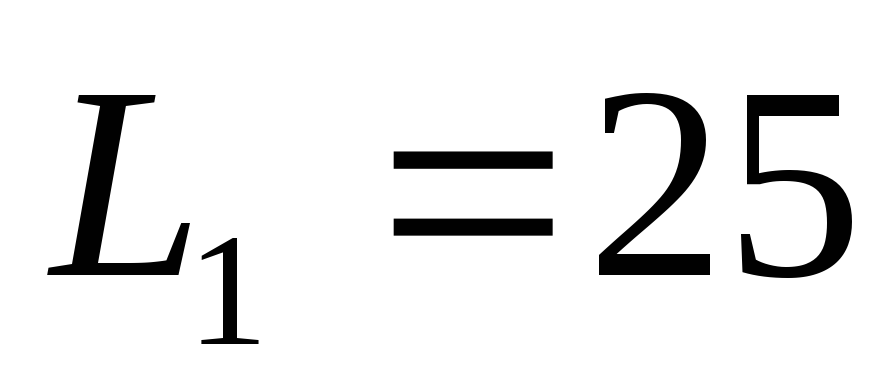 .
Соответствующее количество трудозатрат
находится из решения уравнения (1):
.
Соответствующее количество трудозатрат
находится из решения уравнения (1):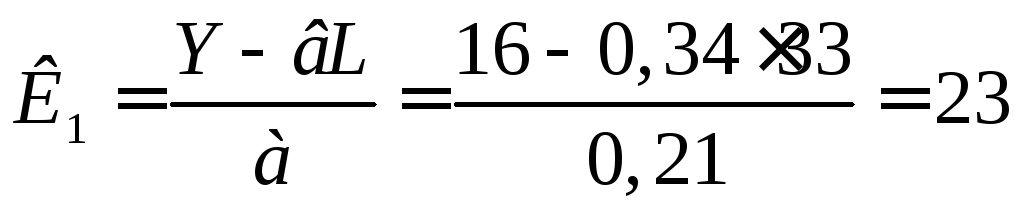 ,
т.е.
,
т.е.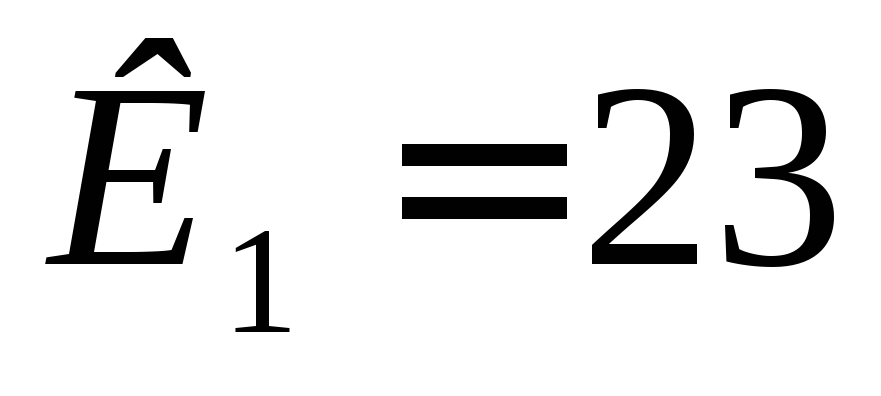 .
.В следующем периоде выпуск увеличим на 25%, предполагая, что затраты ресурса К не ограничены, а трудозатраты должны оставаться на прежнем уровне. Получим, что
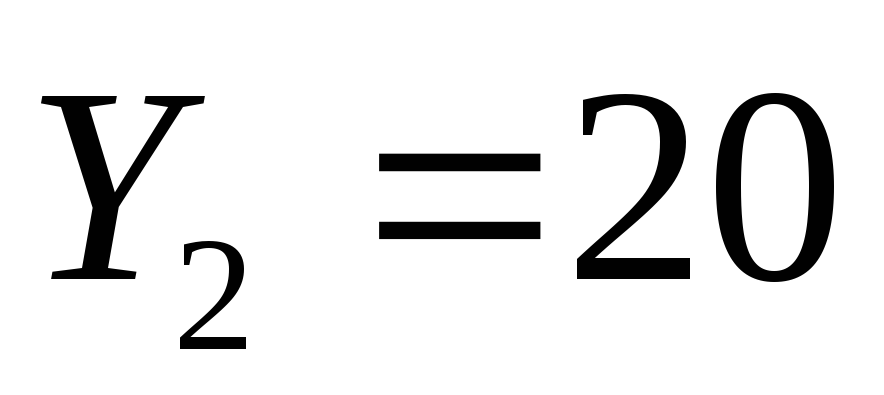 ,
,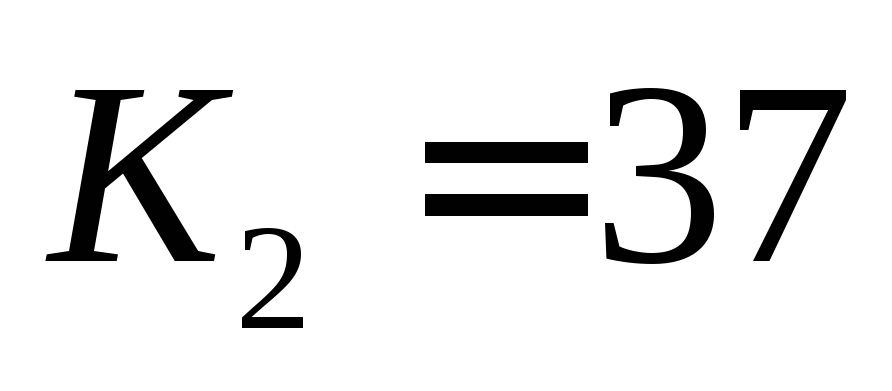 и
и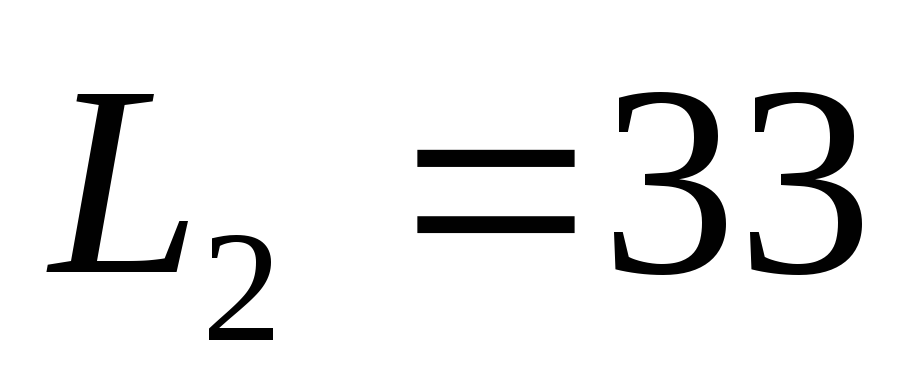 .
.А далее выпуск увеличим еще на 25%,
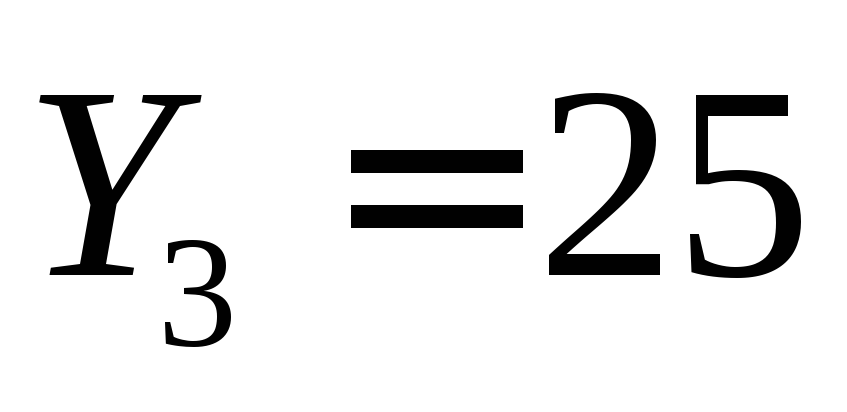 ,
,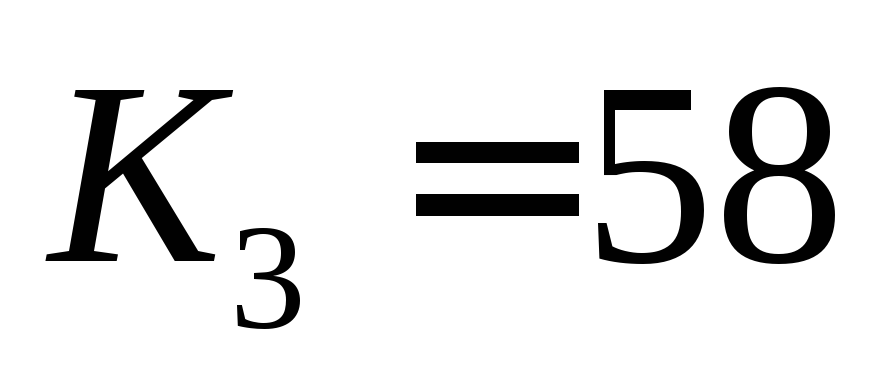 и
и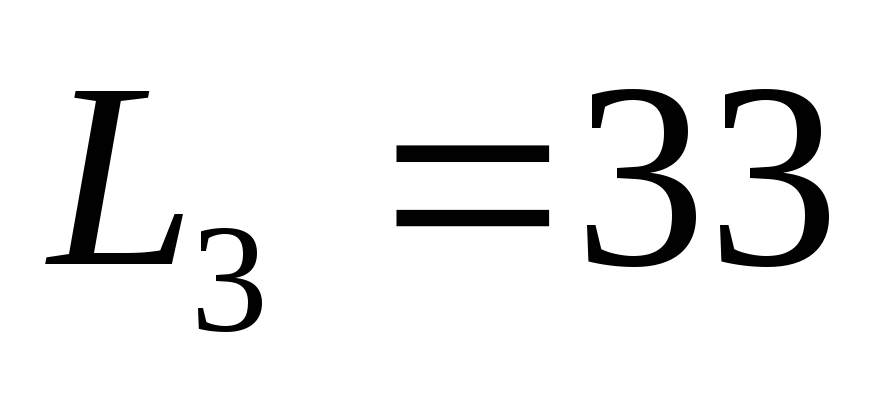 .
.
3.
Определим
средние эффективности производственных
ресурсов
![]() и
и![]() для трех вариантов планов:
для трех вариантов планов:
![]() ,
,
![]() .
.
При
![]() ,
,![]() и
и![]() средняя эффективность ОПФ Фк
=0,69,
а средняя эффективность трудозатрат
Фл=0,64
Т.о., на единицу основных фондов приходится
4 единицы выпуска продукции, а на единицу
трудозатрат 0,64 единиц выпускаемой
продукции.
средняя эффективность ОПФ Фк
=0,69,
а средняя эффективность трудозатрат
Фл=0,64
Т.о., на единицу основных фондов приходится
4 единицы выпуска продукции, а на единицу
трудозатрат 0,64 единиц выпускаемой
продукции.
Средние
эффективности производственных ресурсов
![]() и
и![]() для II и III вариантов рассчитывается
аналогично. Расчеты представлены в
таблице 3.3.
для II и III вариантов рассчитывается
аналогично. Расчеты представлены в
таблице 3.3.
Таблица
3.3 – Расчет средней эффективности
производственных ресурсов
![]() и
и![]()
|
| ||||
|
У |
К |
L |
Фk |
Фл |
|
16 |
23 |
25 |
0,695652 |
0,64 |
|
20 |
37 |
25 |
0,540541 |
0,8 |
|
25 |
58 |
25 |
0,431034 |
1 |
4. Рассчитаем предельные эффективности ресурсов:
![]() ,
,
![]() .
.
Очевидно, что для линейной производственной функции предельные эффективности ресурсов постоянны. Имеет место постоянная отдача от расширения производства. Таким образом, объем выпуска увеличится на 0,21 ед. при изменении затрат ОПФ на единицу и при неизменных затратах труда. Если же затраты труда увеличить на единицу, а ОПФ оставить прежними, то выпуск продукции увеличится на 0,34 ед..
5. Определим коэффициенты эластичности выпуска по ресурсам:
 ,
,
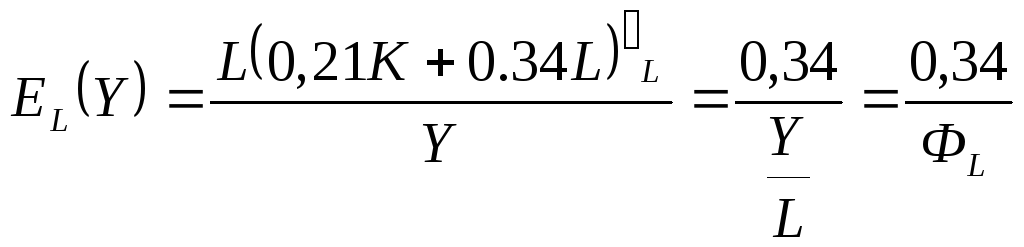 .
.
Для
рассчитываемого базового периода
коэффициент эластичности выпуска по
фондам равен
![]() .
Он показывает, что при увеличении ОПФ
на 1% от 7,36 единиц (
.
Он показывает, что при увеличении ОПФ
на 1% от 7,36 единиц (![]() становится равным
становится равным![]() )
и неизменных затратах труда выпуск
продукции увеличится на 0,4% и составит
16,06 ед..
)
и неизменных затратах труда выпуск
продукции увеличится на 0,4% и составит
16,06 ед..
Коэффициент
эластичности выпуска по труду для
базового периода равен
![]() .
Таким образом, можно утверждать, что
выпуск продукции увеличится на 0,53% от
базового, равного 16, если при неизменных
ОПФ увеличить трудозатраты на 1% от 33.
.
Таким образом, можно утверждать, что
выпуск продукции увеличится на 0,53% от
базового, равного 16, если при неизменных
ОПФ увеличить трудозатраты на 1% от 33.
Расчеты представлены в таблице 3.4.
Таблица 3.4 – Расчет коэффициентов эластичности
|
|
|
|
|
|
|
|
|
У |
К |
L |
Фk |
Фл |
Ek(Y) |
El(Y) |
|
16 |
23 |
25 |
0,695652 |
0,64 |
0,308 |
0,535 |
|
20 |
37 |
25 |
0,540541 |
0,8 |
0,396 |
0,428 |
|
25 |
58 |
25 |
0,431034 |
1 |
0,497 |
0,343 |
6. Определяются предельные нормы замещения ресурсов:
![]() ,
,
![]()
Для линейной ПФ предельные нормы замещения ресурсов не зависят от объемов труда и капитала, т.е. являются постоянными величинами. Для того, чтобы выпуск продукции остался на прежнем уровне, можно затраты труда увеличить на единицу, а высвободить 0,63 ед. основных фондов. Аналогично, увеличение затрат капитала на одну единицу позволяет высвободить 1,6 ед. труда, что сохранит выпуск продукции на прежнем уровне.
7. Построим
изокванты модели при фиксированных
значениях выпуска. Уравнение изокванты
имеет вид:![]() .Для базового
.Для базового
![]() и двух планируемых периодов
и двух планируемых периодов![]() ,
,![]() получаем соответствующие уравнения:
получаем соответствующие уравнения:
![]() ,
,
![]() ,
(1)
,
(1)
![]() .
.
Отсюда считаем L и К для графика
Графиками уравнений (1) являются параллельные прямые. Прямая строится по двум точкам. Возьмем для каждой прямой точки пересечения с координатными осями. Рассчитаем их координаты.(таблица 3. 5)На рисунке 2 представлены изокванты моделей.
Таблица 3.5 – Координаты прямых
|
Y |
K |
L |
|
16 |
0 |
47 |
|
|
76 |
0 |
|
20 |
0 |
59 |
|
|
95 |
0 |
|
25 |
0 |
74 |
|
|
119 |
0 |
рисунок 3.2- изокванты моделей
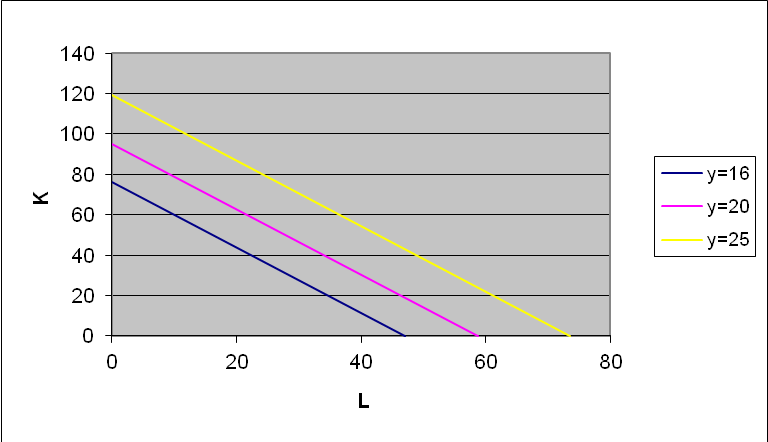
Полученные
прямые показывают различные сочетания
факторов производства
![]() и
и![]() ,
при которых достигается заданный объем
выпуска продукции.
,
при которых достигается заданный объем
выпуска продукции.
