
Пример 3.3
Найти стороны прямоугольника наибольшего периметра, вписанного в окружность радиуса 3
Р ешение.
Введем
систему координат так, как показано на
рисунке 3.2. Тогда окружность имеет
уравнение
ешение.
Введем
систему координат так, как показано на
рисунке 3.2. Тогда окружность имеет
уравнение
![]() .
Пусть 2х
и 2у
– стороны вписанного в эту окружность
прямоугольника. Его периметр равен
.
Пусть 2х
и 2у
– стороны вписанного в эту окружность
прямоугольника. Его периметр равен
![]() .
.
По условию задачи,
вершина
![]() прямоугольника лежит на окружности,
следовательно, ее координаты удовлетворяют
уравнению
прямоугольника лежит на окружности,
следовательно, ее координаты удовлетворяют
уравнению
![]() .
.
Тогда исходную задачу можно сформулировать так:
найти точку
максимума функции
![]() при условии
при условии
![]() .
.
Таким образом, получили задачу на отыскание условного экстремума функции. Решим эту задачу методом множителей Лагранжа. Составим функцию Лагранжа
![]()
и найдем ее безусловный экстремум.
Необходимые условия экстремума в этом случае имеют вид
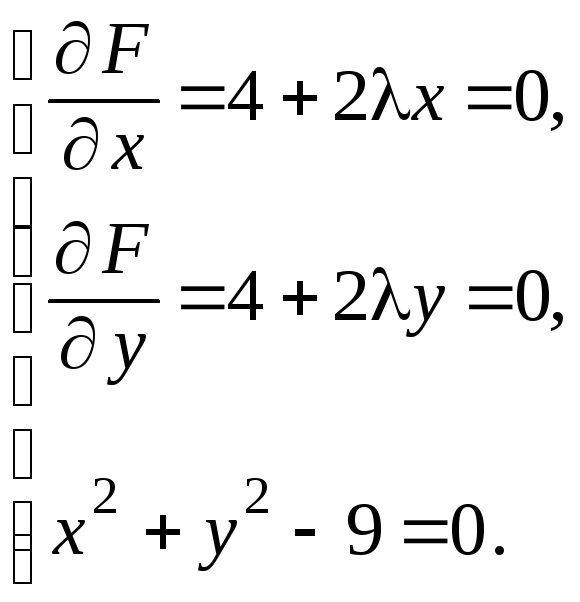
Решая эту систему, получим
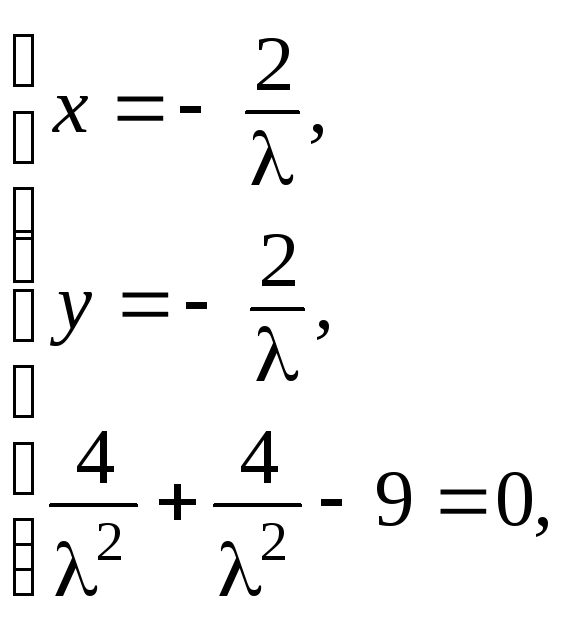
откуда
![]() и
и
![]()
![]()
![]() .
Но так как по условию задачи
.
Но так как по условию задачи
![]() (х
и у
определяют длины сторон прямоугольника),
то имеем единственную критическую точку
(х
и у
определяют длины сторон прямоугольника),
то имеем единственную критическую точку
![]() при
при
![]() .
Проверим выполнение достаточных условий
экстремума. Имеем
.
Проверим выполнение достаточных условий
экстремума. Имеем
![]() ,
,
![]() ,
,
![]() ,
,
отсюда
![]() .
.
При
![]() ,
т.е. в точке
,
т.е. в точке
![]() ,
,
![]() ,
а
,
а
![]() ,
,
значит, точка М
есть точка максимума функции
![]() и, следовательно, точка условного
максимума функции
и, следовательно, точка условного
максимума функции
![]() .
.
Таким образом, из
всех прямоугольников, вписанных в
окружность радиуса 3, наибольший периметр
имеет квадрат со стороной, равной
![]() .
.
Пример 3.4
Найти наибольшее
и наименьшее значения функции
![]() в области, ограниченной линиями
в области, ограниченной линиями
![]() ,
,
![]() ,
,
![]() .
.
Р ешение.
Для
наглядности построим область. Каждое
из уравнений
ешение.
Для
наглядности построим область. Каждое
из уравнений
![]() ,
,
![]() ,
,
![]() определяет на плоскости прямую; построив
эти прямые получим искомую область –
треугольник АОВ (рисунок 3.3, обозначим
эту область Q).
Заметим, что областью определения
заданной функции является вся плоскость
ХОУ, значит, эта функция определена в
области Q.
определяет на плоскости прямую; построив
эти прямые получим искомую область –
треугольник АОВ (рисунок 3.3, обозначим
эту область Q).
Заметим, что областью определения
заданной функции является вся плоскость
ХОУ, значит, эта функция определена в
области Q.
Будем решать задачу, используя аналитический метод. Найдем критические точки функции. Имеем
![]() ,
,
![]() .
.
Эти производные
не существуют при
![]() ,
следовательно, точка
,
следовательно, точка
![]() – критическая точка функции. Но, очевидно,
условия
– критическая точка функции. Но, очевидно,
условия
![]() приводят к той же точке
приводят к той же точке
![]() .
Значит, других критических точек функция
.
Значит, других критических точек функция
![]() не имеет.
не имеет.
Точка
![]() принадлежит области Q
и является «угловой» точкой этой
области. Вычислим значение функции в
этой точке:
принадлежит области Q
и является «угловой» точкой этой
области. Вычислим значение функции в
этой точке:
![]() .
.
Исследуем функцию на границе области Q.
а) Участок АВ
границы имеет уравнение
![]() ,
или
,
или
![]() ,
где
,
где
![]() .
Подставив это значение у
в функцию
.
Подставив это значение у
в функцию
![]() ,
получим функцию одной переменной
,
получим функцию одной переменной
![]() ,
,
![]() .
.
Найдем критические точки этой функции
![]() .
.
Легко убедиться,
что дискриминант квадратного трехчлена
![]() отрицателен, поэтому производная
отрицателен, поэтому производная
![]() определена на всем промежутке
определена на всем промежутке
![]() .
Значит, критические точки функции
.
Значит, критические точки функции
![]() находим только из условия
находим только из условия
![]() ,
т.е. решив уравнение
,
т.е. решив уравнение
![]() ,
откуда
,
откуда
![]() .
Из уравнения
.
Из уравнения
![]() находим
находим
![]() и получаем точку
и получаем точку
![]() ,
лежащую на участке АВ границы области
Q.
Вычислим значение функции
,
лежащую на участке АВ границы области
Q.
Вычислим значение функции
![]() в этой точке
в этой точке
![]() .
.
б) Аналогично
рассмотрим участок ВО, на нем
![]() ,
,
![]() ,
функция
,
функция
![]() примет вид
примет вид
![]() (т.к.
(т.к.
![]() ).
).
Тогда
![]() ,
критических точек нет.
,
критических точек нет.
в) На участке ОА
![]() ,
подставив это значение в функцию
,
подставив это значение в функцию
![]() ,
получим
,
получим
![]() (т.к.
(т.к.![]() в области Q),
в области Q),
![]() ,
,
следовательно, на этом участке границы также нет критических точек.
«Угловыми» точками
области Q,
наряду с точкой
![]() ,
являются точки А
,
являются точки А![]() и В
и В![]() ,
вычислим значения функции в этих точках:
,
вычислим значения функции в этих точках:
![]() ,
,
![]() .
.
Сравнивая все полученные значения функции
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
приходим к выводу,
что наименьшее значение функции равно
нулю и достигает его функции в точке
![]() ,
а наибольшее значение равно 8, достигается
в точке В
,
а наибольшее значение равно 8, достигается
в точке В![]() .
Итак,
.
Итак,
![]() ,
,
![]() .
.
