
Пример 1.6
Указать точки разрыва функции.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
Решение.
а)
Функция
![]() элементарная, поэтому точками
разрыва ее
являются точки, в которых функция не
определена. Область определения данной
функции есть вся координатная плоскость,
кроме точки
элементарная, поэтому точками
разрыва ее
являются точки, в которых функция не
определена. Область определения данной
функции есть вся координатная плоскость,
кроме точки
![]() – это и есть точки разрыва данной
функции.
– это и есть точки разрыва данной
функции.
б)
Функция
![]() определена и непрерывна для тех значений
х
и у,
для которых выполняется неравенство
определена и непрерывна для тех значений
х
и у,
для которых выполняется неравенство
![]() ,
которое, очевидно выполняется, при
условии
,
которое, очевидно выполняется, при
условии
![]() ,
или
,
или
![]() .
.
Но уравнение
![]() ,
или
,
или
![]() определяет эллипс с центром в начале
координат и полуосями
определяет эллипс с центром в начале
координат и полуосями
![]() .
Следовательно, получили линию
разрыва –
эллипс
.
Следовательно, получили линию
разрыва –
эллипс
![]() .
.
в)
Область непрерывности функции трех
переменных
![]() образует множество точек трехмерного
пространства, координаты которых
удовлетворяют условию
образует множество точек трехмерного
пространства, координаты которых
удовлетворяют условию
![]() .
Рассмотрим уравнение
.
Рассмотрим уравнение
![]() ,
или
,
или
![]()
– это уравнение
однополостного гиперболоида, точки
которого и являются точками разрыва
заданной функции. Таким образом, имеем
поверхность
разрыва –
гиперболоид
![]() .
.
Пример 2.1
Найти частные производные первого порядка функции:
а)
![]() ; б)
; б)
![]() .
.
Решение. а) Основной принцип нахождения частной производной функции нескольких переменных заключается в следующем:
чтобы найти производную функции по одной из ее переменных, нужно все остальные переменные считать постоянными и дифференцировать функцию по тем же правилам и формулам, по которым вычисляется производная функции одной переменной.
Используем этот принцип:
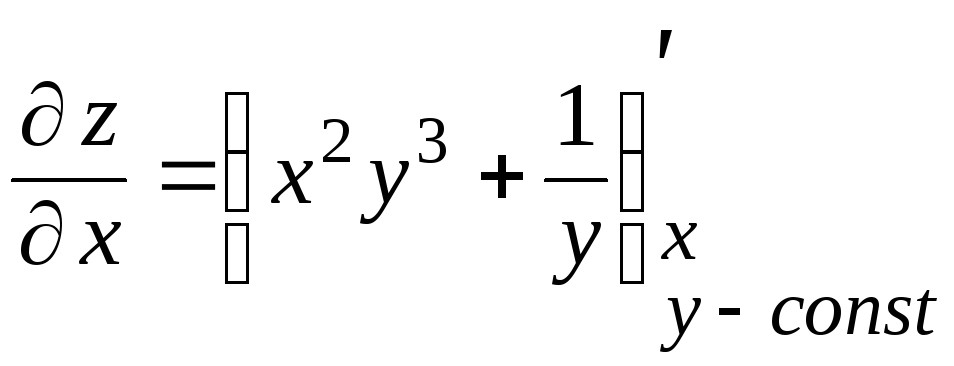 =
=![]() ,
,
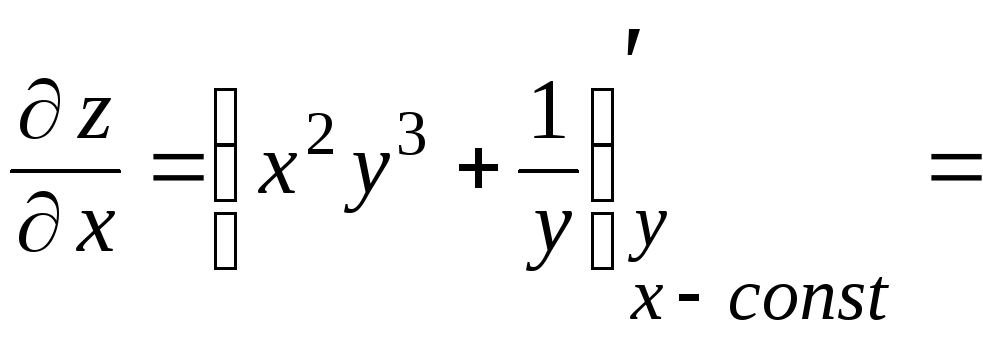
![]()
![]() .
.
б) Аналогично находим
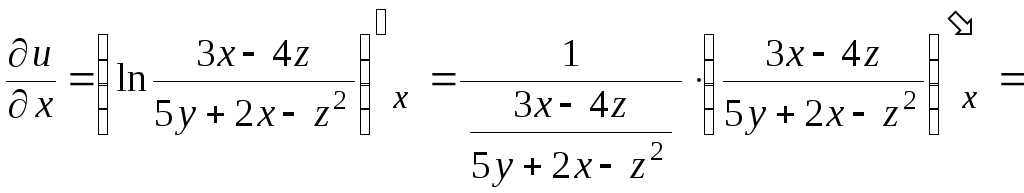
![]()
![]()
![]()
![]() ;
;
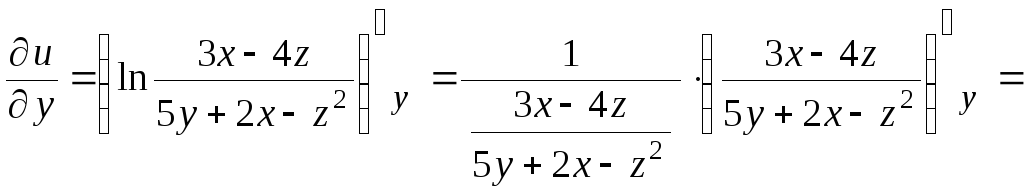
![]()
![]() ;
;
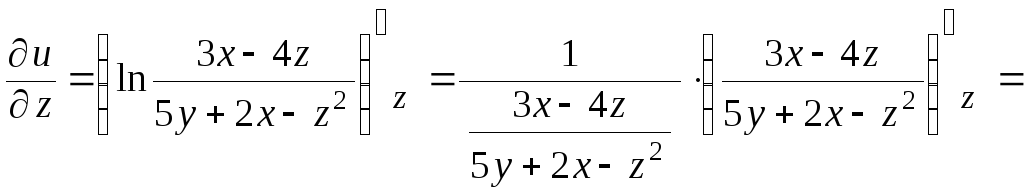
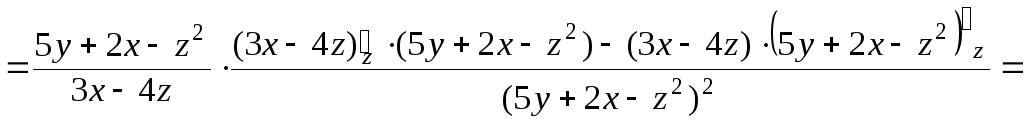
![]() .
.
Пример 2.2
Найти стационарные
точки функции
![]() .
.
Решение. Стационарными называют точки области определения функции, в которых частные производные первого порядка от данной функции по всем ее аргументам равны нулю.
Областью определения данной функции является, очевидно, вся координатная плоскость ХОУ.
Найдем частные производные этой функции:
![]() ,
,
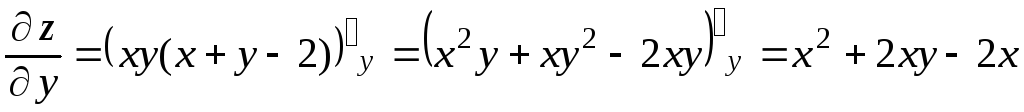 .
.
Составим и решим
систему уравнений
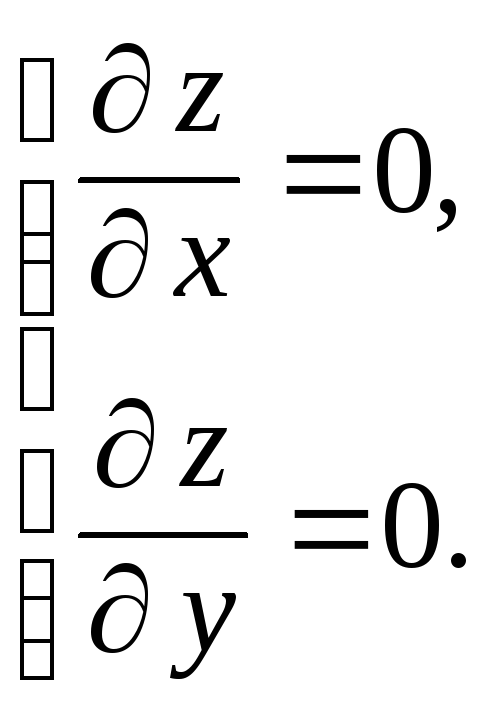
Получим
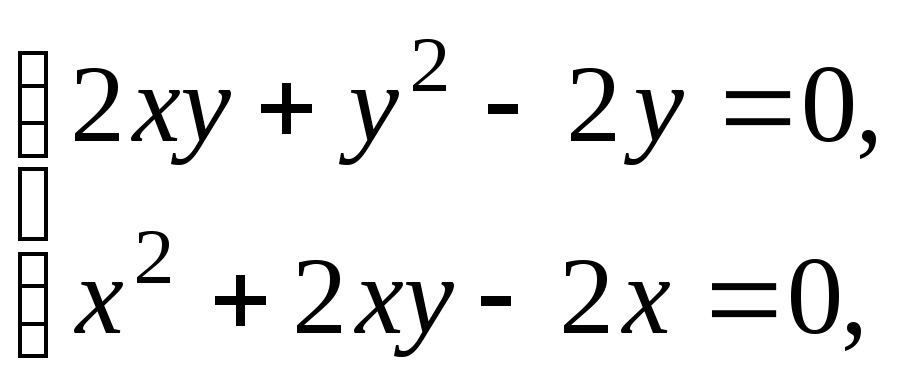
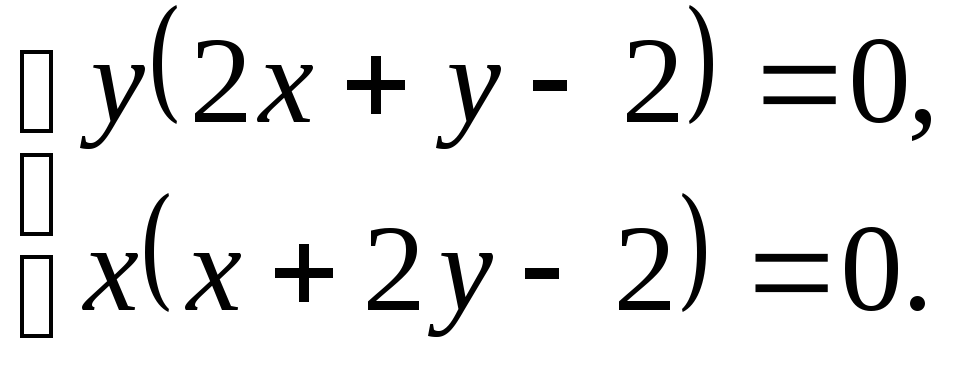 Из первого уравнения системы находим
Из первого уравнения системы находим
![]() или
или
![]() .
.
Если
![]() ,
то второе уравнение системы примет вид
,
то второе уравнение системы примет вид
![]() ,
откуда
,
откуда
![]() или
или
![]() .
Получим точки
.
Получим точки
![]() .
.
Если
![]() ,
откуда
,
откуда
![]() ,
то второе уравнение решаемой системы
примет вид
,
то второе уравнение решаемой системы
примет вид
![]() ,
или
,
или
![]() ,
откуда
,
откуда
![]() или
или
![]() .
При
.
При
![]() получим
получим
![]() ;
при
;
при
![]() получим
получим
![]() .
Значит, получили еще две точки
.
Значит, получили еще две точки
![]() ,
,
![]() .
.
Таким образом,
данная функция имеет четыре стационарные
точки
![]() ,
,
![]() ,
,
![]() .
.
Пример 2.3
Найти все частные производные второго порядка функции
![]() .
.
Решение. Сначала необходимо найти производные первого порядка по каждой переменной:
![]()
![]() ,
,
![]() .
.
Теперь найдем производные второго порядка, продифференцировав полученные функции по каждой переменной:
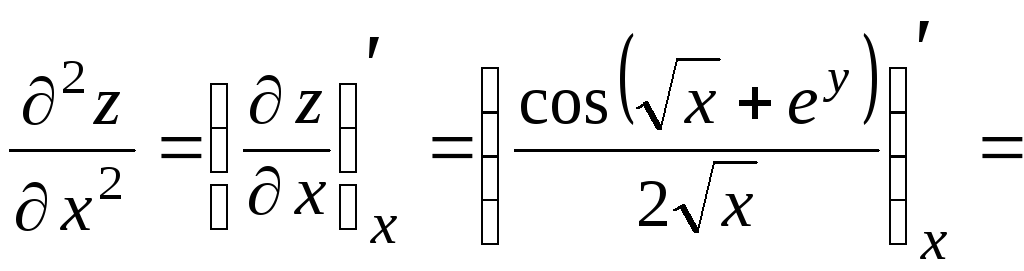
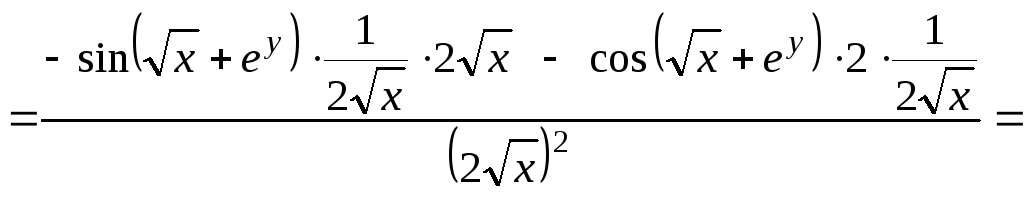
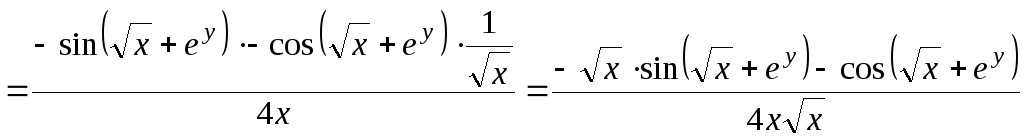 ,
,
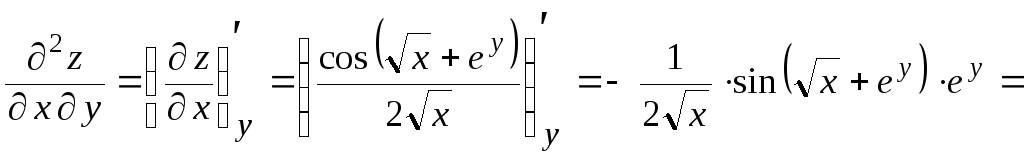
=
![]() ,
,
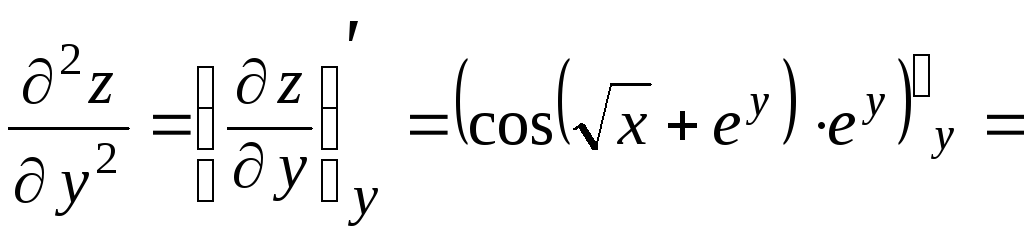
![]() ,
,
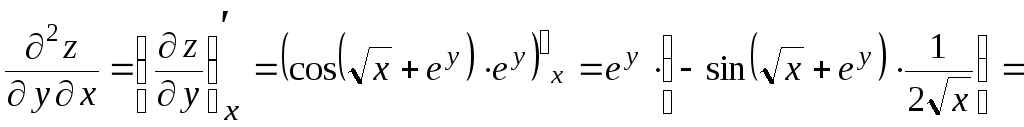
![]() .
.
Обратите внимание
на равенство производных
![]() и
и
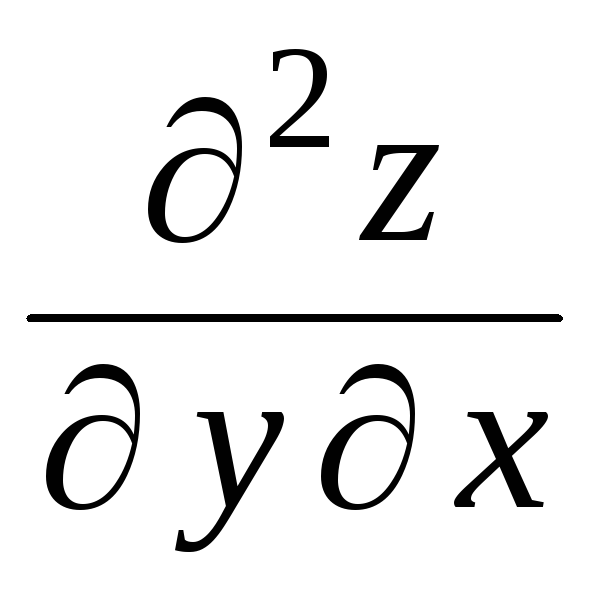 .
.
Пример 2.4
Доказать, что
функция
![]() удовлетворяет уравнению
удовлетворяет уравнению
.
![]() .
.
Решение. Функция удовлетворяет данному уравнению, если при подстановке в это уравнение и самой функции, и ее производных указанного вида уравнение обращается в тождество (равенство, справедливое для любых допустимых значений переменных).
Найдем необходимые частные производные:
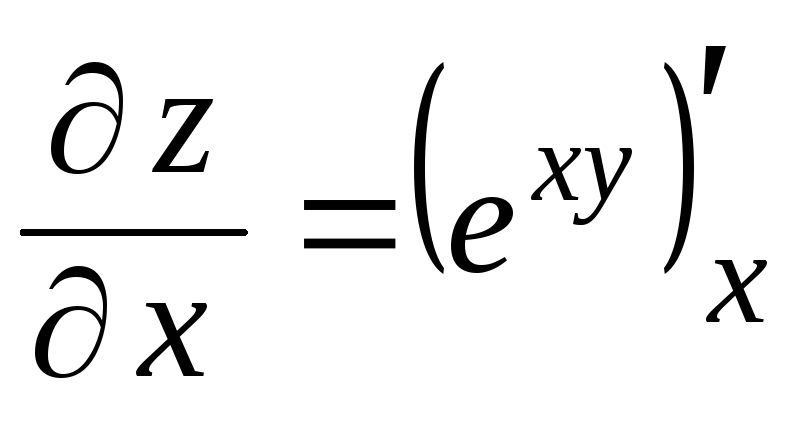 =
=
![]()
![]() ,
,
![]() =
=
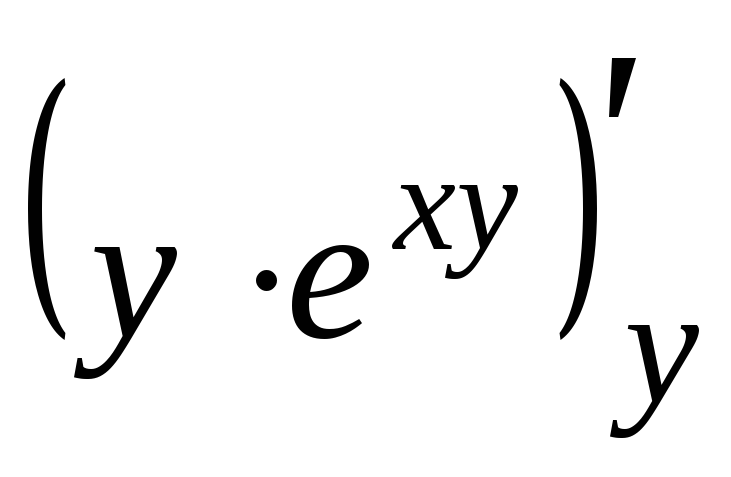 =
=
![]() ,
,
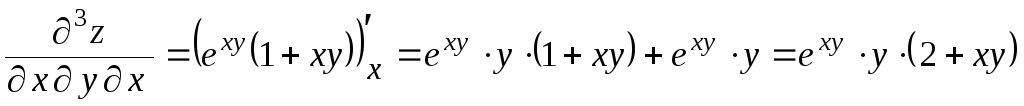 ;
;
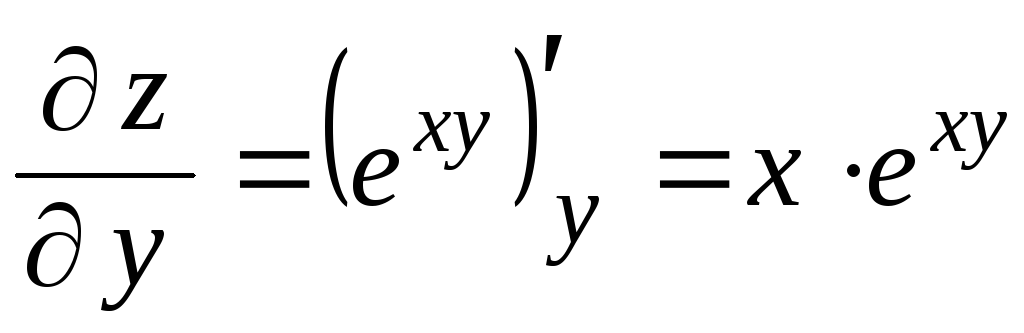 ,
,
![]() =
=
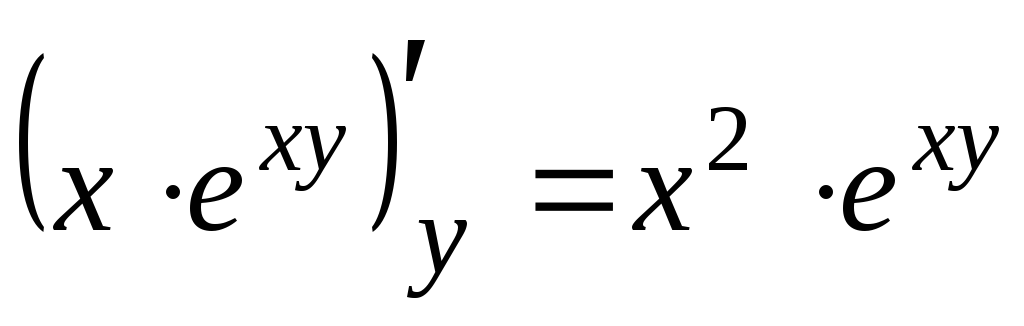 ,
,
![]()
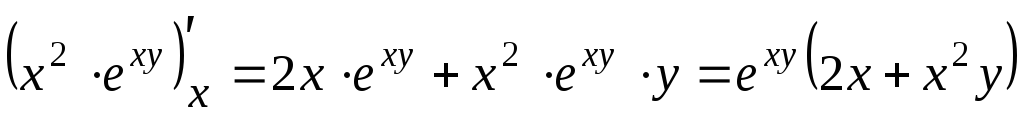 .
.
Тогда левая часть заданного уравнения примет вид
![]()
![]()
Правая же часть уравнения для данной функции имеет вид
![]() .
.
Очевидно,
![]() – получили тождество, значит, заданная
функция удовлетворяет уравнению.
– получили тождество, значит, заданная
функция удовлетворяет уравнению.
Пример 2.5
Найти производные первого порядка для функций, заданных неявно и вычислить их значения в точке (0, 1):
а)
![]() ;
;
б)
![]() .
.
Решение.
а)
Используем
информацию: если функция z
задана неявно уравнением
![]() ,
то ее частные
производные первого порядка равны
,
то ее частные
производные первого порядка равны
:
![]() ,
,
![]() .
.
В нашем случае
![]()
![]() .
Тогда
.
Тогда
![]()
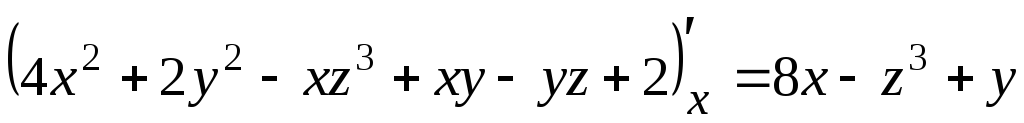 ,
,
![]()
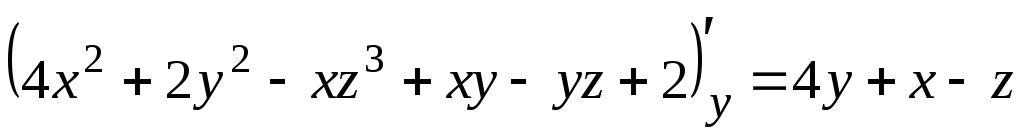 ,
,
![]()
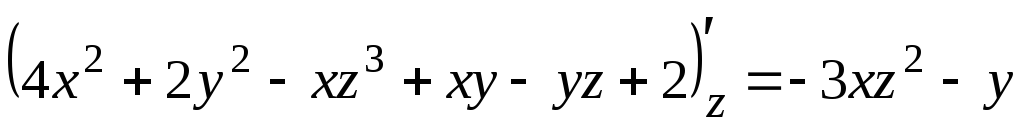 .
.
Тогда
![]() ,
,
![]() .
.
Чтобы вычислить
значения этих частных производных в
точке (0, 1), найдем сначала значение
функции z
в этой точке. Для этого используем
уравнение
![]() .
Полагая здесь
.
Полагая здесь
![]() ,
,
![]() ,
получим
,
получим
![]() ,
,
![]() ,
,
откуда
![]() .
Тогда
.
Тогда
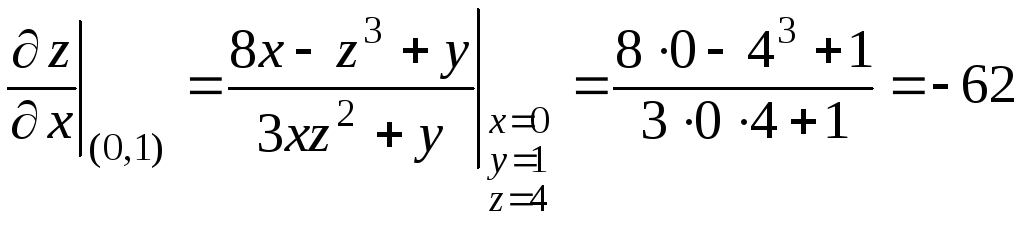 ,
,
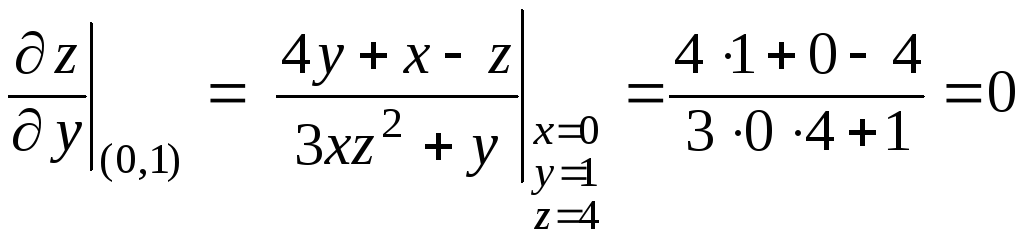 .
.
б)
Если у
есть неявная функция переменной х,
заданная уравнением
![]() ,
то ее производная
первого порядка равна
,
то ее производная
первого порядка равна
![]() .
.
Используя эту
формулу, найдем производную функции у
переменной
х
заданной неявно формулой
![]() .
Здесь
.
Здесь
![]()
![]() .
.
Тогда
![]()
![]() ,
,
![]()
![]() ,
,
следовательно
![]() =
=
![]() .
.
Найдем значение производной в точке (0, 1)
![]()
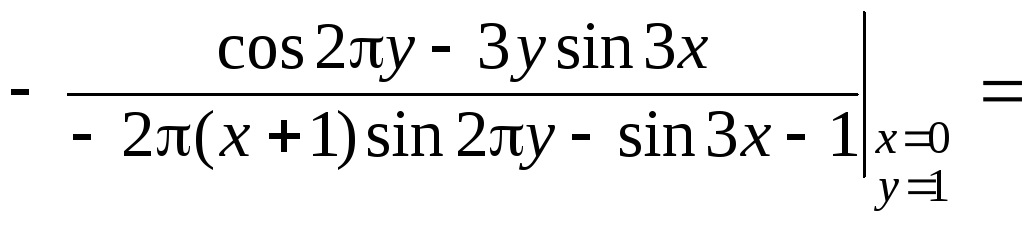
![]() .
.
