
Пример 5.1
Подобрать эмпирическую формулу для описания зависимости между величинами х и у по данным эксперимента:
-
х
1
2
3
4
5
6
7
у
7,5
6,4
6,1
5,9
5,5
4
3,5
Решение. На координатную плоскость ХОУ нанесем точки, соответствующие данным таблицы:
![]() ,
(2; 6,4), (3; 6,1), (4; 5,9), (5; 5,5), (6; 4),
(7; 3,5).
,
(2; 6,4), (3; 6,1), (4; 5,9), (5; 5,5), (6; 4),
(7; 3,5).
По характеру
расположения этих точек можно сделать
предположение, что переменные х
и у
связаны линейной зависимостью
![]() ,
причем
,
причем
![]() ,
т.к. величина у
убывает с возрастанием х
(рисунок 5.2). Для отыскания параметров
а
и b
применим метод наименьших квадратов.
,
т.к. величина у
убывает с возрастанием х
(рисунок 5.2). Для отыскания параметров
а
и b
применим метод наименьших квадратов.
 Составим
функцию
Составим
функцию
![]() .
.
Найдем точку минимума этой функции. Используем необходимые условия экстремума:
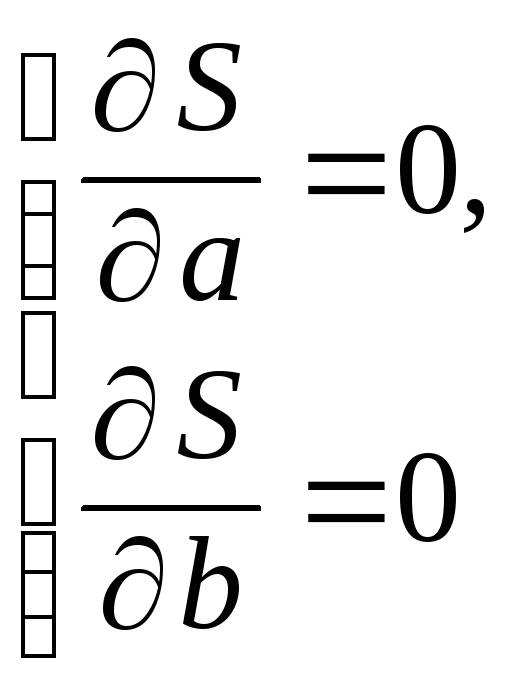
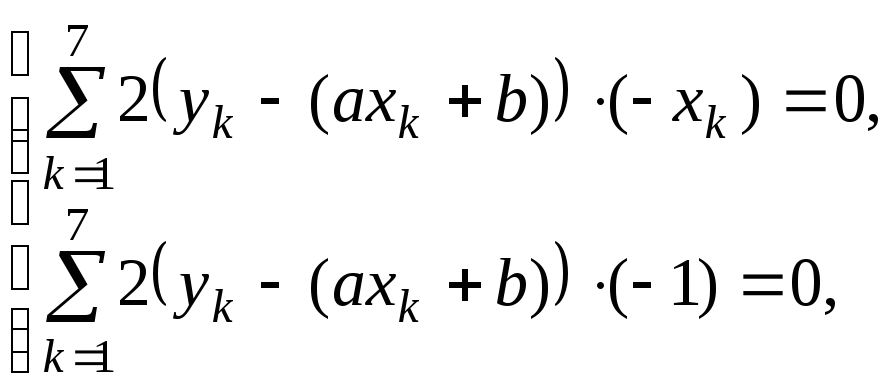
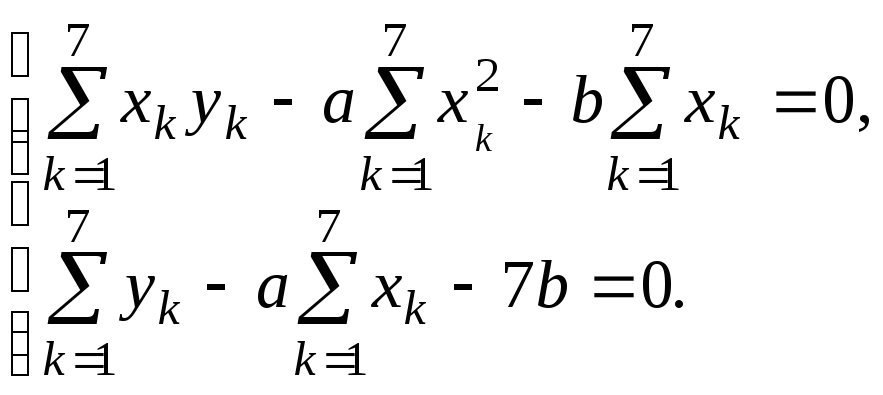
Для вычисления сумм удобно составить таблицу:
-
№
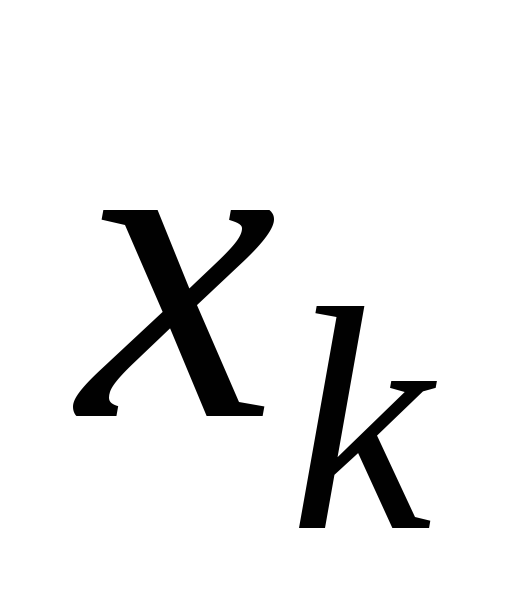
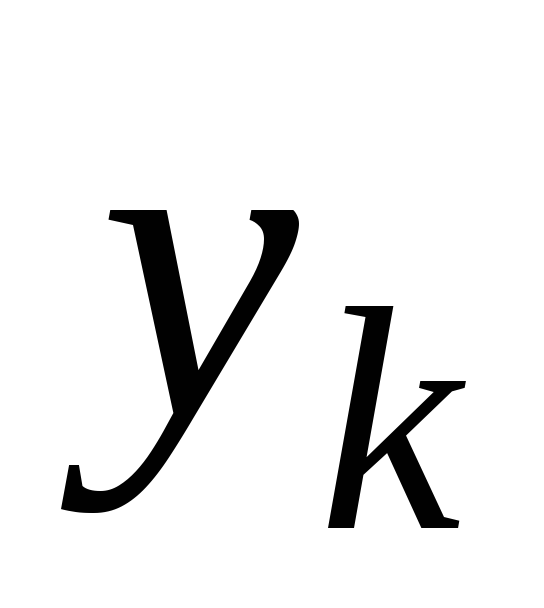
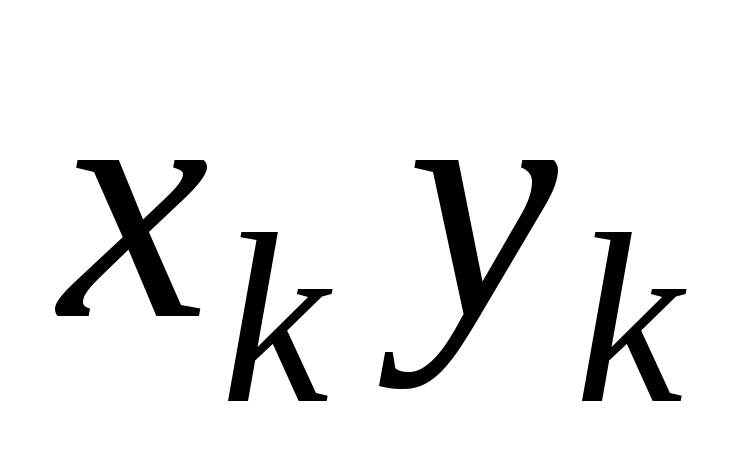
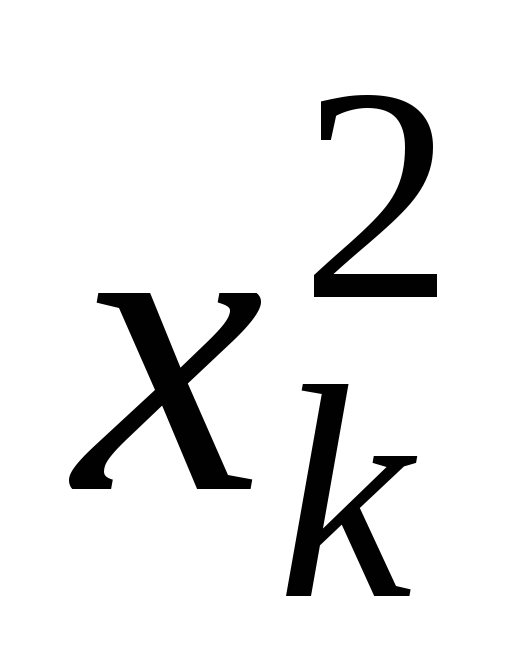
1
1
7,5
7,5
1
2
2
6,4
12,8
4
3
3
6,1
18,3
9
4
4
5,9
23,6
16
5
5
5,5
27,5
25
6
6
4
24
36
7
7
3,5
24,5
49
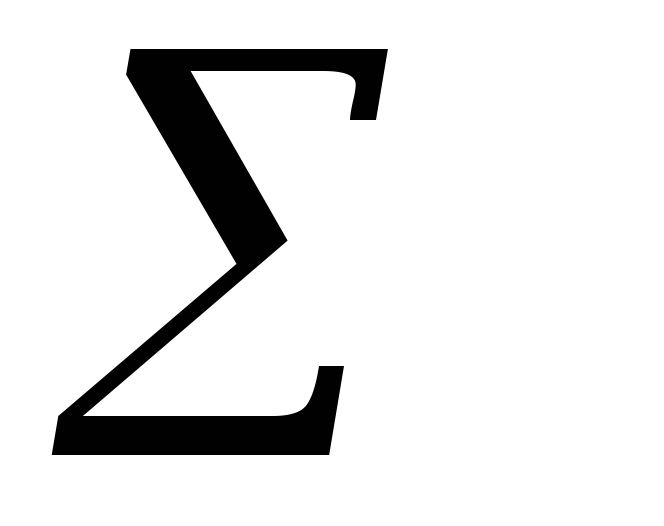
28
38,9
138,2
140
Тогда система уравнений для отыскания параметров а и b примет вид
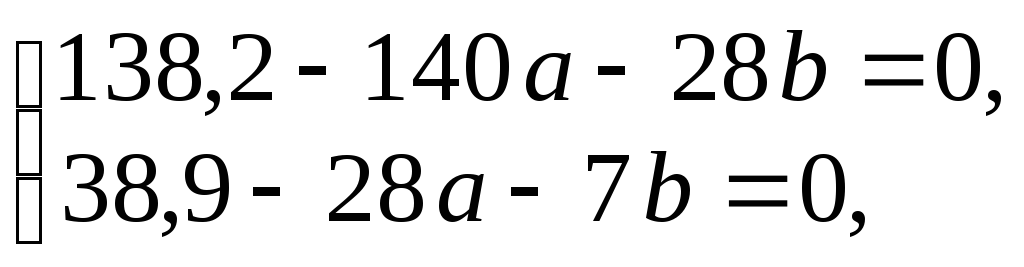 или
или
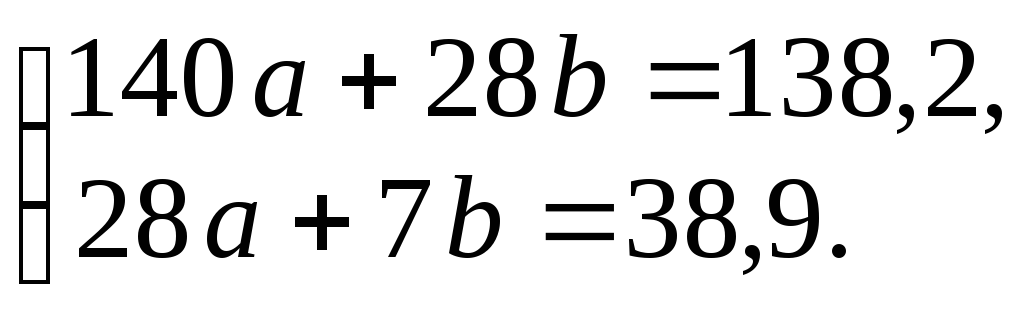
Решая эту систему,
получим![]() .
Таким образом, искомая эмпирическая
формула имеет вид
.
Таким образом, искомая эмпирическая
формула имеет вид
![]() .
.
Пример 5.2
Измерение температуры корпуса работающего агрегата, производимые с интервалом 5 минут, дало следующие результаты:
-
t, мин
5
10
15
20
25
Т, С
59,3
59,8
60,1
64,9
70,2
Считая, что зависимость между температурой и временем квадратичная, найти формулу, описывающую эту зависимость.
Решение.
Квадратичная
зависимость между переменными Т
и
t
можно описать формулой
![]() .
Параметры
.
Параметры
![]() этой зависимости найдем методом
наименьших квадратов.
этой зависимости найдем методом
наименьших квадратов.
Составим функцию
![]() .
.
Чтобы найти точку минимума этой функции, используем необходимые условия экстремума:
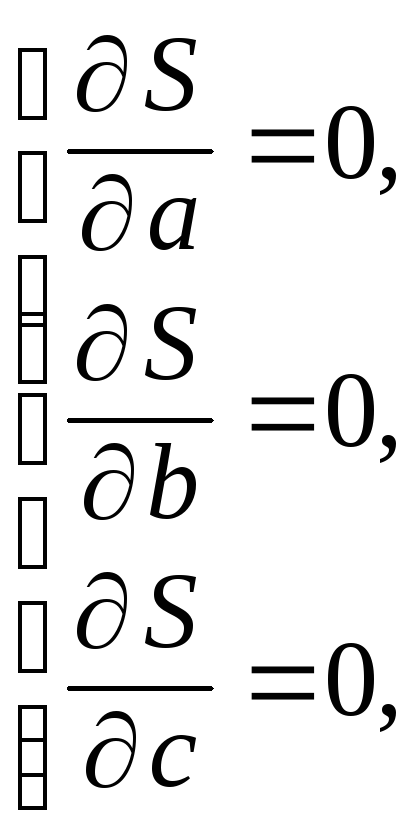
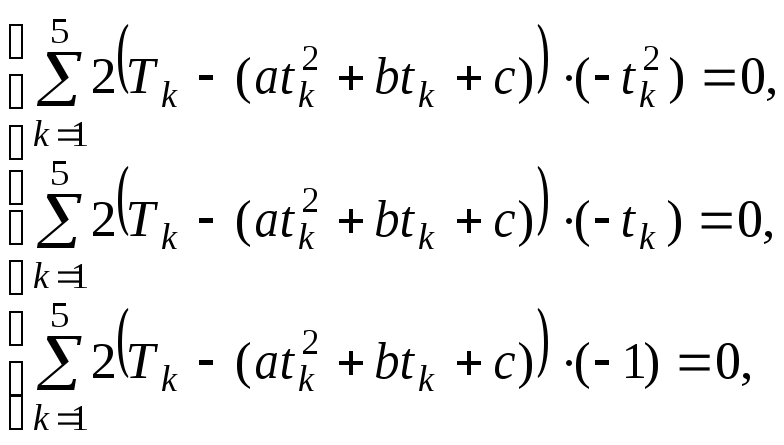
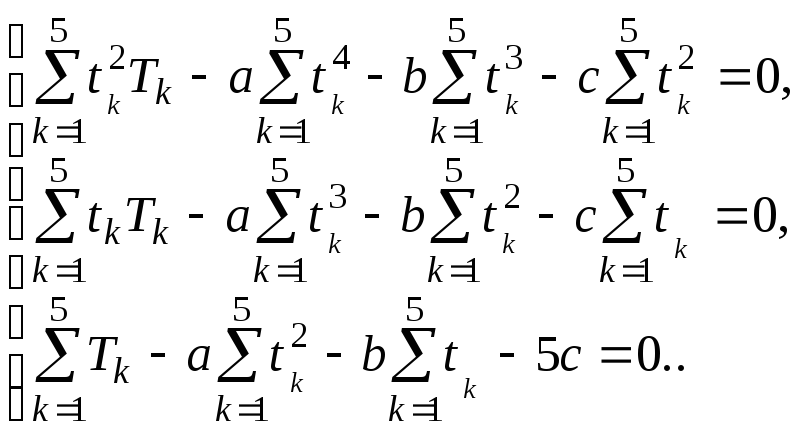
Для вычисления сумм составим таблицу:
|
№ |
|
|
|
|
|
|
|
|
1 |
5 |
59,3 |
25 |
125 |
625 |
296,5 |
1482,5 |
|
2 |
10 |
59,8 |
100 |
1000 |
10000 |
598 |
5980 |
|
3 |
15 |
60,1 |
225 |
3375 |
50625 |
901,5 |
13522,5 |
|
4 |
20 |
64,9 |
400 |
8000 |
160000 |
1298 |
25960 |
|
5 |
25 |
70,2 |
625 |
15625 |
390625 |
1755 |
43875 |
|
|
75 |
314,3 |
1375 |
28125 |
611875 |
4849 |
90820 |
Тогда система
уравнений относительно параметров
![]() имеет вид
имеет вид
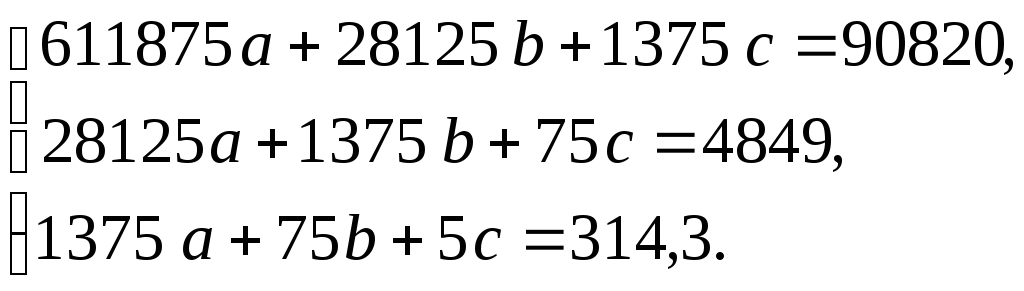
Решая эту систему,
получаем
![]() .
Таким образом, искомая зависимость
выражается формулой
.
Таким образом, искомая зависимость
выражается формулой
![]() .
.
