Лекция 2 Определители

6

Лекция 2. определители

1. Определители второго порядка

2. Определители третьего порядка

3. Алгебраические дополнения и миноры

4. Разложение определителя по строке или столбцу

5. Свойства определителей

6. Обратная матрица

7. Свойства обратной матрицы

1. Определители второго порядка

Понятие определителя вводится только для квадратной матрицы.

Определитель – это число, которое считается по определенным правилам. Порядок определителя – это порядок квадратной матрицы. Если для задания матриц использовались круглые скобки, то в теории определителей используют прямые скобки.

Каждой квадратной матрице поставим в соответствие некоторое число, которое будем называть определителем матрицы, и укажем правило его вычисления. Обозначения:

• Дана матрица _. Определителем второго порядка называется число, вычисляемое по правилу:

.

Пример 1. .

2. Определители третьего порядка

• Дана матрица . Определителем третьего порядка называется число, вычисляемое по правилу:

В каждом произведении нет чисел из одного столбца или одной строки.

Приведем схему для запоминания порядка получения слагаемых в определителе.

Произведение чисел на одной диагонали берется со знаком «+» (это главная диагональ матрицы), а на другой – с противоположным знаком.

Пример 2.

3. Алгебраические дополнения и миноры

Для вычисления определителей порядка больше третьего применяют другие способы вычисления.

• Минором элемента определителя называется определитель , полученный из определителя вычеркиванием -ой строки и -го столбца, на пересечении которых стоит элемент .

Пример 3. Минор определителя есть .

• Алгебраическим дополнением элемента определителя называется минор , умноженный на :

.

Полезно запомнить, что и .

Пример 4. В примере 3 алгебраическое дополнение

.

4. Разложение определителя по строке или столбцу

Вычисление определителя -го порядка можно свести к вычислению определителей порядка , используя следующие формулы.

1. Разложение определителя по -й строке:

Это число равно сумме произведений элементов любой -й строки на их алгебраические дополнения.

Пример 5. Вычислить определитель третьего порядка разложением по первой строке.

Решение

2. Разложение определителя по -му столбцу:

Это число равно сумме произведений элементов любого -го столбца на их алгебраические дополнения.

Независимо от способа разложения всегда получается один и тот же ответ.

5. Свойства определителей

1. При транспонировании квадратной матрицы ее определитель не меняется: .

Вывод. Свойства определителей, сформулированных для строк, справедливы и для столбцов.

2. При перестановке двух строк (столбцов) определитель меняет знак на противоположный. Например, _.

3. Определитель равен нулю, если:

а) он имеет нулевую строку (столбец) ;

б) он имеет пропорциональные (одинаковые) строки (столбец) .

4. Общий множитель в строке (столбце) можно выносить за знак определителя. Например, .

5. Определитель не изменяется, если к элементам какой-либо строки прибавить (вычесть) соответствующие элементы другой строки, умноженные на любое число.

Например, .

6. Если в определителе каждый элемент строки есть сумма двух слагаемых, то этот определитель равен сумме двух определителей:

.

7. Определитель произведения двух квадратных матриц одного и того же порядка равен произведению определителей этих матриц:

.

8. Определитель квадратной матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали:

.

6. Обратная матрица

Вместо операции деления матриц вводится понятие обратной матрицы.

• Если при умножении квадратных матриц _и в любом порядке получается единичная матрица (_{), то матрица} называется обратной матрицей для квадратной матрицы , а _{матрица - обратная для матрицы .}

Обозначается обратная матрица _{, то есть .}

Очевидна аналогия с числами: для числа 2 число ½ есть обратное, так как . Именно поэтому матрица, обратная к А, обозначается _.

Теорема «Необходимое и достаточное условие существования обратной матрицы». Для того чтобы квадратная матрица имела обратную матрицу, необходимо и достаточно, чтобы определитель матрицы был не равен нулю.

Правило нахождения обратной матрицы

0) Смотрим, является ли матрица квадратной. Если нет, то обратной матрицы не существует; если квадратная, то переходим к пункту 1.

1) Вычисляем определитель матрицы : если он не равен нулю, то обратная матрица существует: _{; если равен нулю, то обратной матрицы нет.}

2) Для каждого элемента матрицы вычисляем его алгебраическое дополнение .

3) Составляем матрицу из алгебраических дополнений, которая затем транспонируем: _.

4) Каждый элемент матрицы делим на определитель : _{Получаем матрицу, обратную данной.}

7. Нахождение обратной матрицы для матриц второго порядка

Пример 6. Дана матрица . Найти обратную матрицу.

Решение.

Проверка. Убедимся, что найдена действительно обратная матрица. Найдем произведение матриц и .

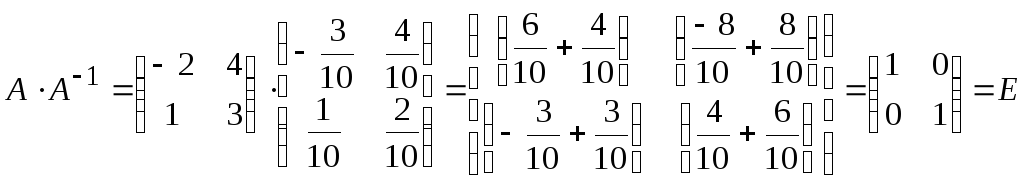
8. Свойства обратной матрицы

1. ,

где А и В – невырожденные квадратные матрицы одинакового порядка.

2. .

3. .

4. .

Контрольные вопросы

1. Что называется определителем второго порядка?

2. Как вычислить определитель третьего порядка?

3. Как вычислить определитель 3 порядка по правилу треугольников?

4. Что называется алгебраическим дополнением элемента определителя? Приведите примеры для определителей 2 и 3 порядков.

5. Напишите разложения определителя третьего порядка по элементам произвольной строки и произвольного столбца.

6. Сформулируйте основные свойства определителей.

7. В каком случае определители равны нулю? Приведите примеры.

8. Представьте определитель в виде суммы двух определителей.

9. Заполните пропущенные места так, чтобы значения определителей были одинаковы: и .

10. Запишите определитель третьего порядка треугольного вида. Как его вычислить?

11. Какая матрица называется обратной для данной матрицы?

12. Для любой ли квадратной матрицы существует обратная?

13. Пусть . Будут ли матрицы и взаимно обратными?

14. При каких значениях параметра существует матрица, обратная матрице ?

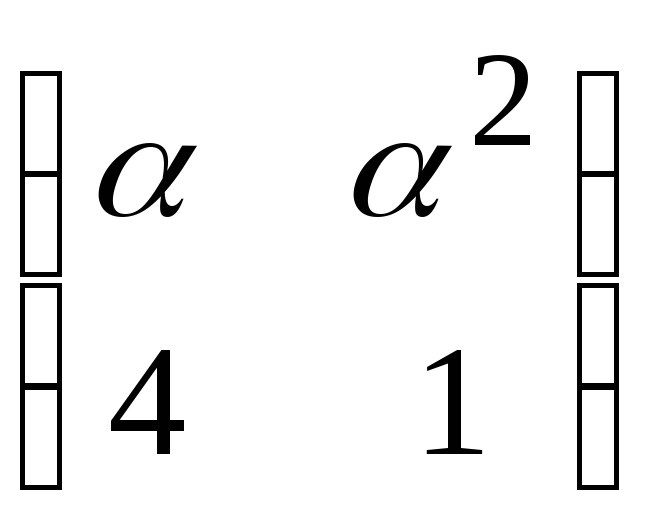15. Запишите формулу для нахождения обратных матриц 2 и 3 порядков.

16. Сформулируйте правило нахождения обратной матрицы.