
матем Матрицы 1 модуль_8
.doc
Министерство образования и науки Российской Федерации
ФГБОУ ВПО «Сибирский государственный технологический университет»
М.М. БАБКина
Математика
Сборник задач к практическим занятиям (1-й семестр)
Красноярск
2014-15 уч. год
Содержание практических занятий
Модуль 1. Линейная АЛГЕБРА
6 недель, 3 лекции, 6 практич. занятий
-
Проверочная работа по школьному курсу 2 ч
-
Матрицы, операции над ними 2 ч
-
Определители: вычисление и свойства 2 ч
-
Системы линейных уравнений. Метод определителей (Крамера) 2 ч
-
Системы линейных уравнений. Метод исключения неизвестных (Гаусса) 2 ч
-
Контрольная работа № 1 «Линейная алгебра» 2 ч
Модуль 2. Векторы и аналитическая геометрия
6 недель, 3 лекции, 6 практич. занятий
-
Векторы на плоскости 2 ч
-
Прямая на плоскости 2 ч
-
Взаимное расположение прямых. Графическое решение систем линейных неравенств.
-
Кривые второго порядка 2 ч
-
Контрольная работа № 2 «Векторы и аналитическая геометрия» 2 ч
-
* Задачи с экономическим содержанием 2 ч
Модуль 3. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
6 недель, 3 лекции, 6 практич. занятий
-
Функции одной переменной: область определения и значений, свойства функции 2 ч
-
Графики функций одной переменной 2 ч
-
Предел функции 2 ч
-
Контрольная работа №3 «Введение в математический анализ» 2 ч
-
Зачетное занятие 2 ч
-
Зачетное занятие 2 ч
Модуль 1. линейная алгебра
Практическое занятие 1.
проверочная работа по школьному курсу
Тема «Линейные уравнения и неравенства, их системы»
Образец варианта
Часть 1. Линейные уравнения и их системы
№1. (1 балл) Какое из уравнений является линейным уравнением с двумя переменными?
А)
3х + 5у = 10; Б) ху = 20; В) 4х + 3 = 15; Г)
х![]() +у
+у![]() =17.
=17.
№2. (1 балл) Через какую из данных точек проходит график функции х + 4у = 14?
А) А(6; 3); Б) В(-10; 6); В) С(7; 7); Г) К(0; 4).
№3.
(1 балл) Какая из пар чисел является
решением системы уравнений
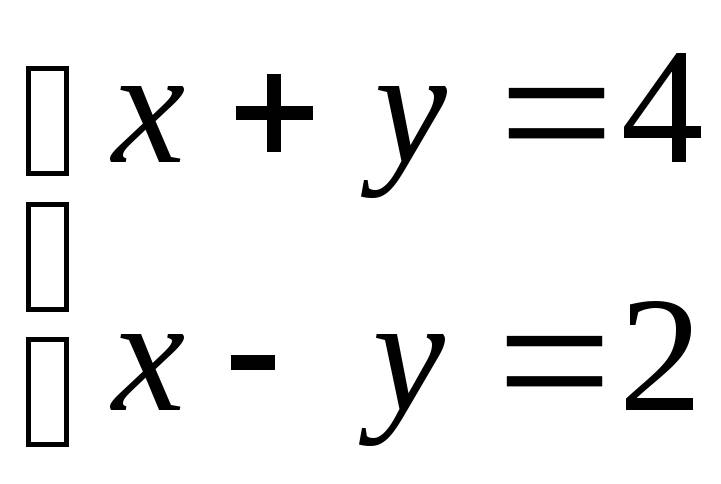 ?
?
А) (-2; 0); Б) (0; -5); В) (3; 1); Г) другой ответ.
№4.
(2
балла)
Решите
систему уравнений:
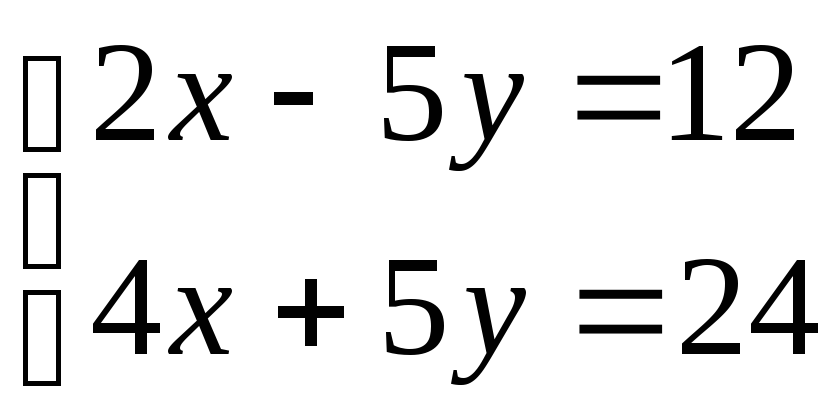 .
.
№5.
(3
балла)
Постройте график функции
![]() .
Пользуясь построенным графиком,
установите, при каких значениях аргумента
функция принимает положительные
значения.
.
Пользуясь построенным графиком,
установите, при каких значениях аргумента
функция принимает положительные
значения.
Часть 2. Линейные неравенства и их системы
№1.
(1 балл) Если
![]() ,
то для любых
,
то для любых
![]() и
и
![]() верно неравенство:
верно неравенство:
![]() №2.
(1 балл) Решите
неравенство
№2.
(1 балл) Решите
неравенство
![]() .
.
![]()
№3.
(2 балла)
Найдите наименьшее целое решение системы
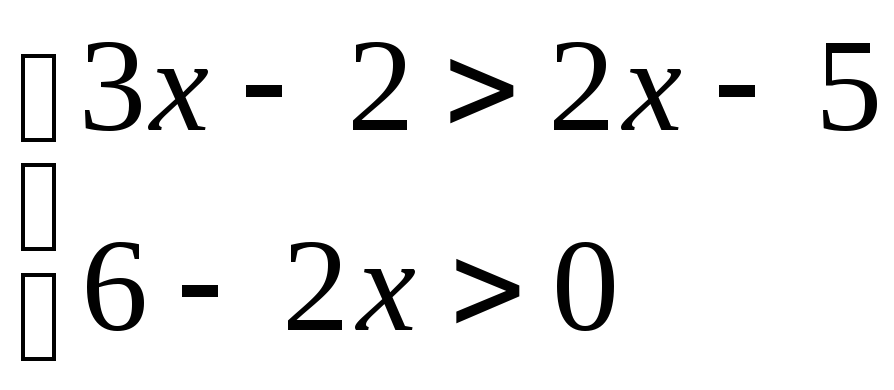
![]()
№4. (3 балла) Для каждой системы неравенств укажите множество ее решений.
1.
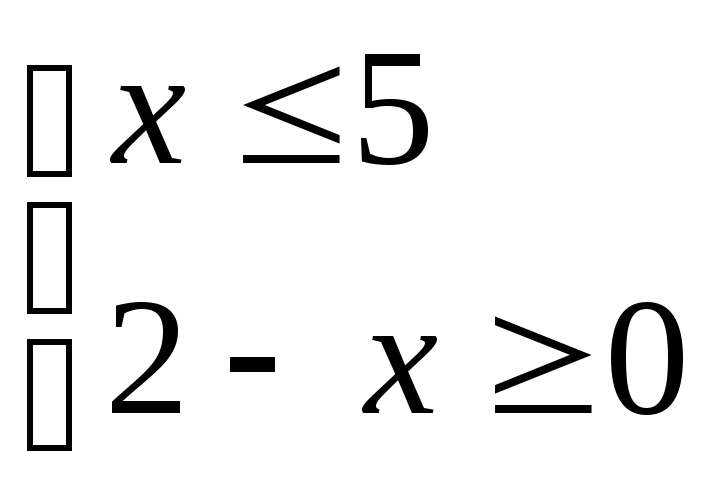 2.
2.
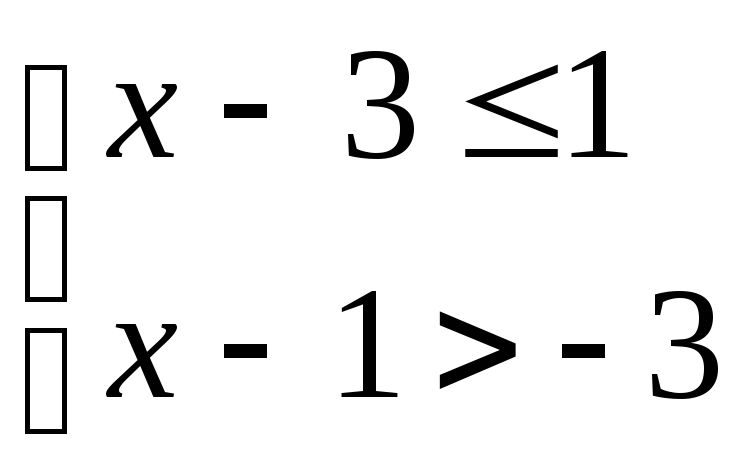 3.
3.
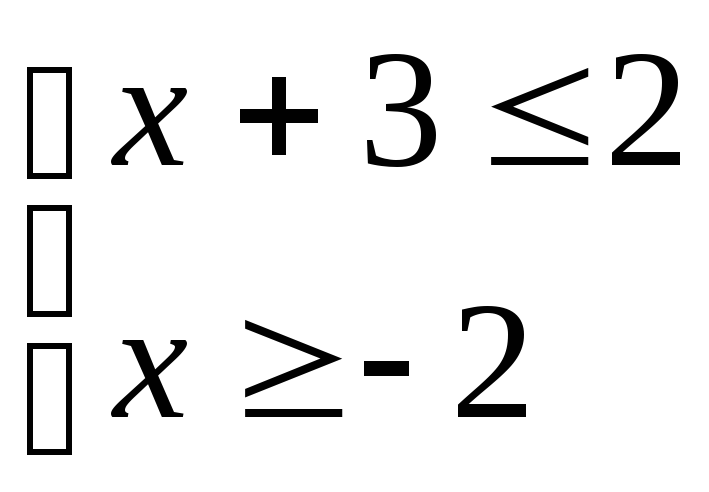
А. (-2; 4]; Б. [-2; -1]; В [-3; 5]; Г. (-∞; 2].
Практическое занятие 2.
Матрицы, операции над ними
Задачи для решения на занятии
№1.
Даны матрицы
![]() ,
,
![]() и единичная матрица
и единичная матрица
![]() .
.
Найти
матрицы
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
1)
![]() ;
;
2)
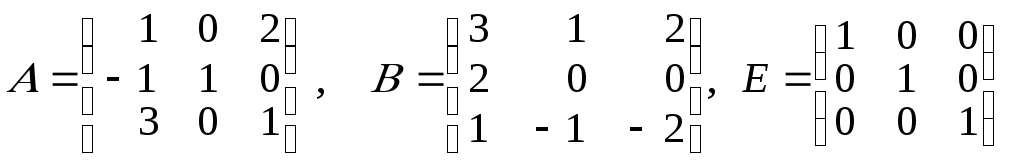 .
.
№2. Найти произведение матриц.
1)
![]() 2)
2)
![]()
3)
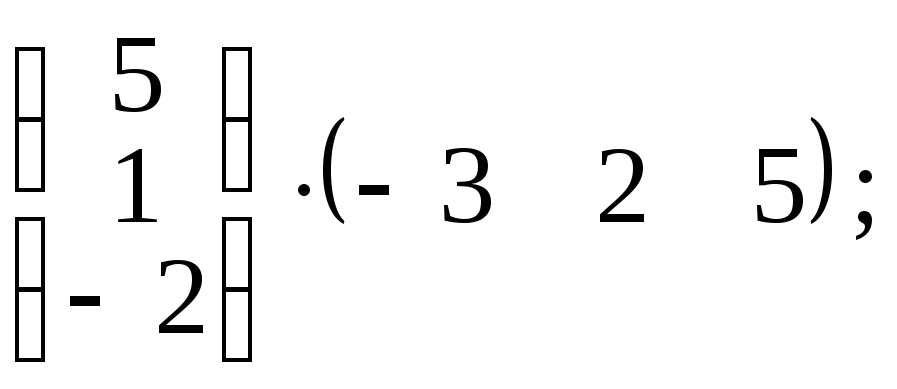 4)
4)
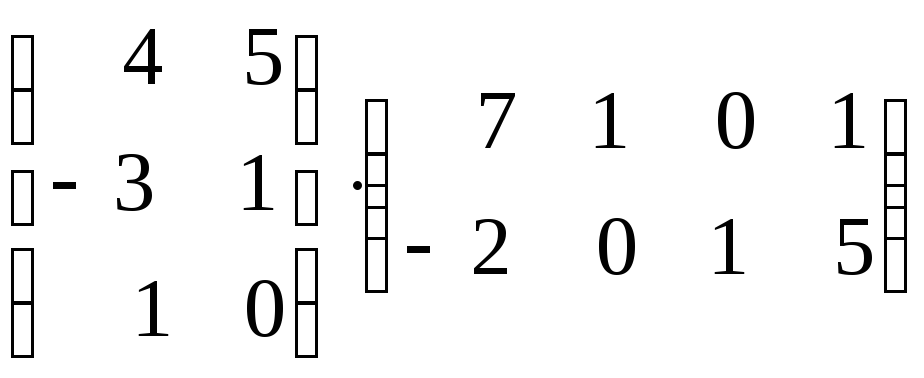 .
.
Задачи для домашнего решения
№3. Даны матрицы А, В и единичная матрица Е.
Найти
матрицы ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
1)
![]() ;
2)
;
2)
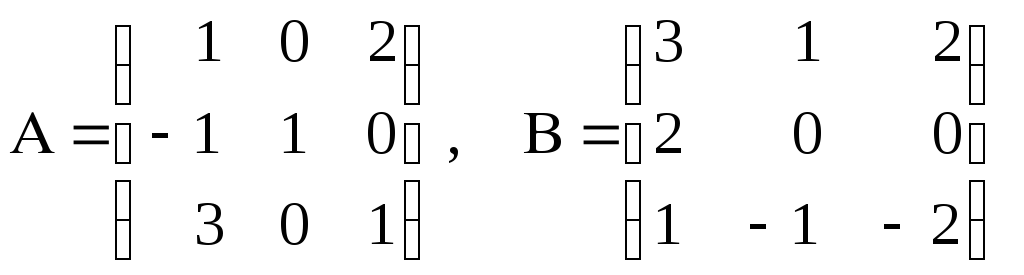 .
.
№4. Найти произведение матриц.
1)
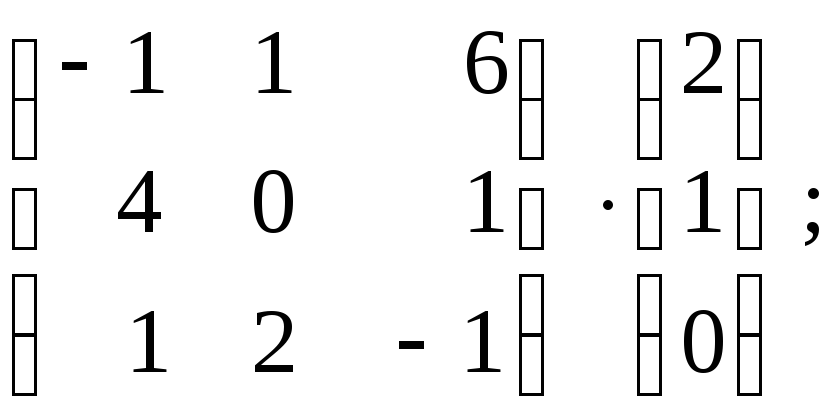 2)
2)
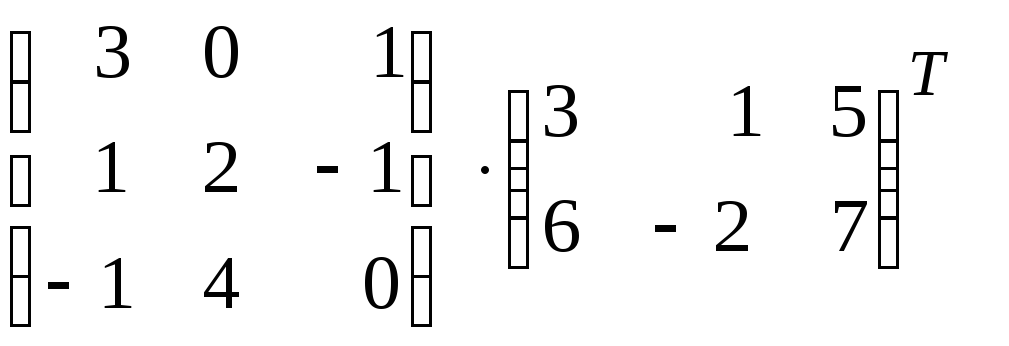 ;
;
3)
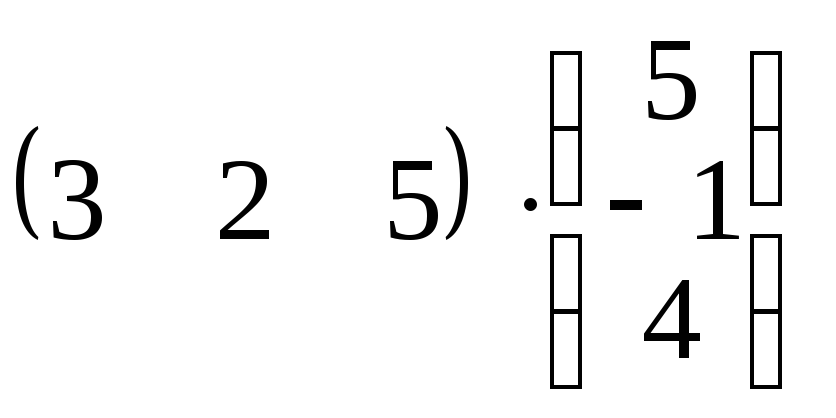 ; 4)
; 4)
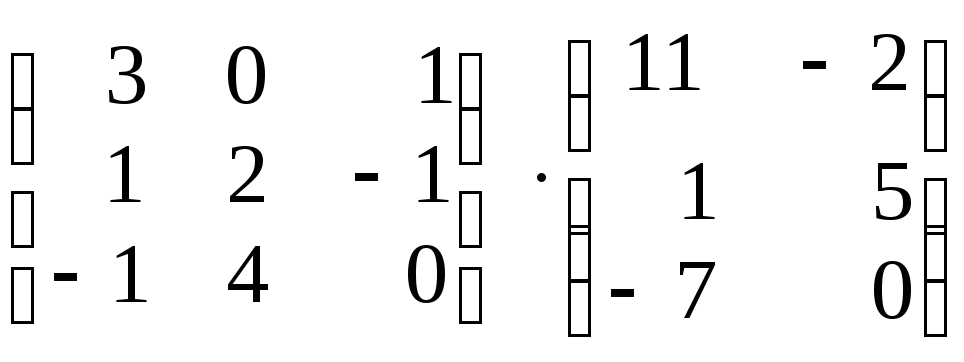 .
.
№5.
Даны
матрицы
![]() и
и
![]() .
Найти матрицу
.
Найти матрицу
![]() ,
являющуюся решением уравнением
,
являющуюся решением уравнением
![]() .
.
Практическое занятие 3.
Определители: вычисление и свойства
Задачи для решения на занятии
№1. Вычислить определители второго порядка:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
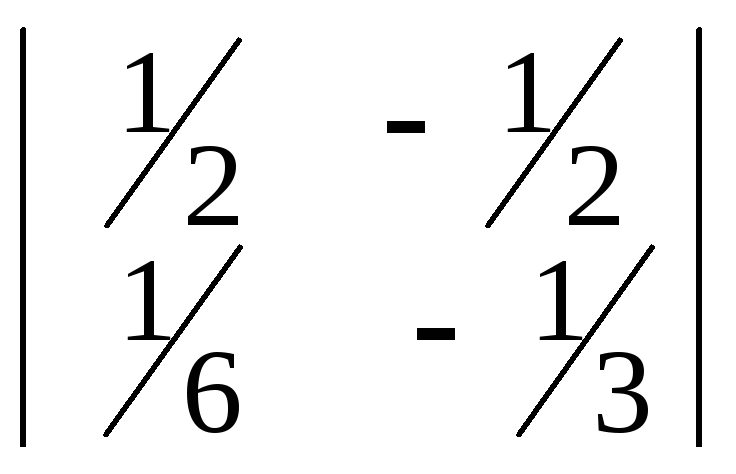 .
.
№2. Вычислить определители третьего порядка по правилу треугольников.
1)
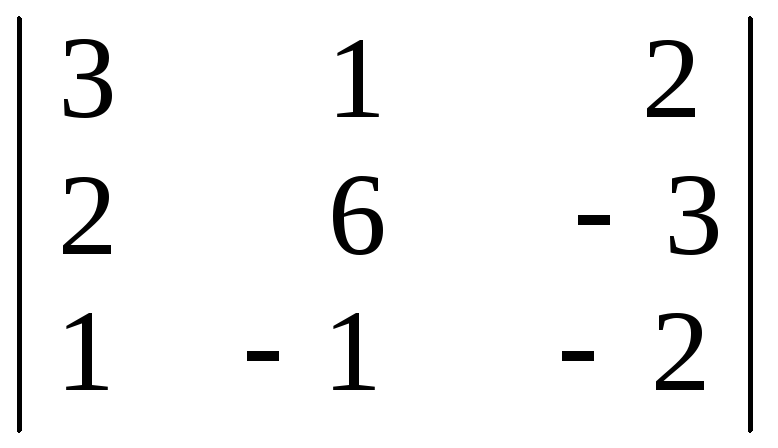 ;
2)
;
2)
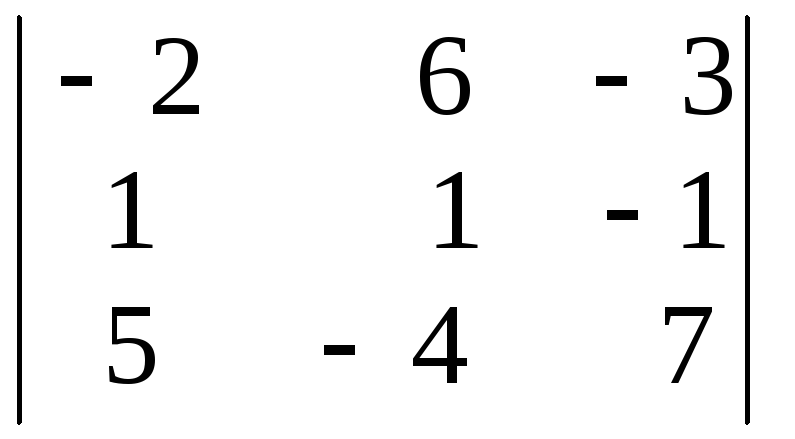 .
.
№3.
Дан определитель
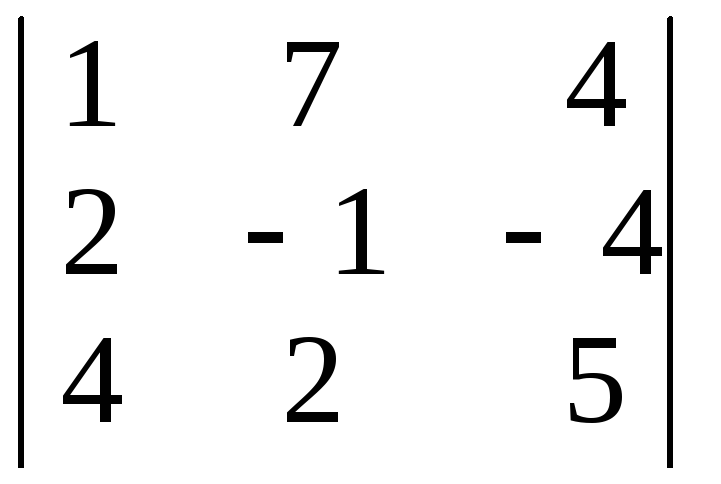 .
Вычислить все алгебраические дополнения
для элементов; а) первой строки, б) второго
столбца.
.
Вычислить все алгебраические дополнения
для элементов; а) первой строки, б) второго
столбца.
№4. Вычислить определители, используя теорему о разложении по элементам строки или столбца.
1)
 ;
2)
;
2)
 .
.
Задачи для домашнего решения
№5. Вычислить определители второго порядка:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)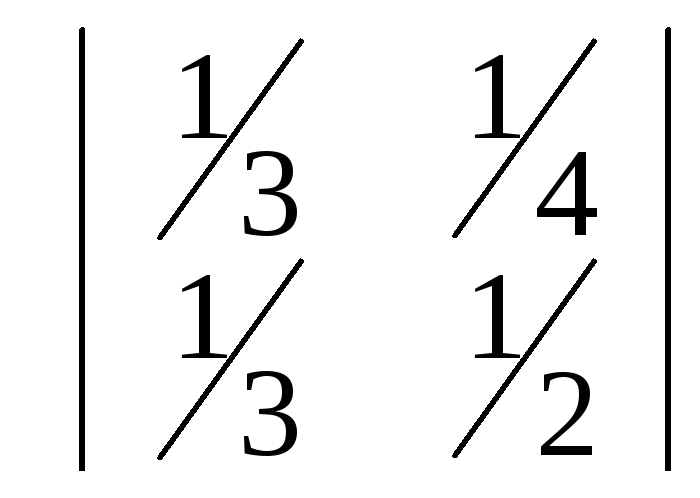 ;
4)
;
4)
![]() ;
5)
;
5)
![]() .
.
№6.
Найти, при каком значении
![]() определитель
определитель
![]() равен нулю.
равен нулю.
№7. Вычислить определители третьего порядка двумя способами:
а) по правилу треугольников; б) используя теорему о разложении.
1)
 ;
2)
;
2)
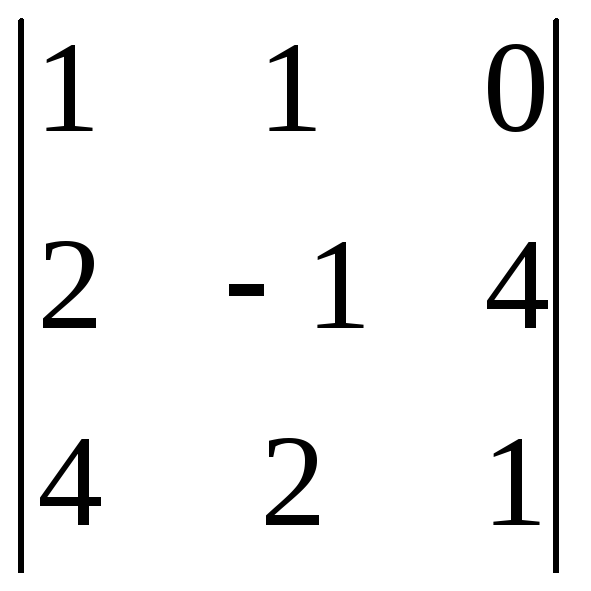 .
.
№8.
Записать
выражение для определителя
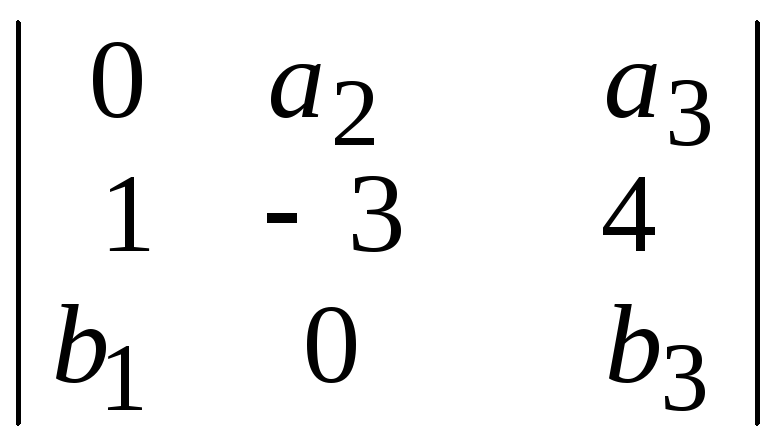 .
.
Практическое занятие 4.
Системы линейных уравнений. Метод Крамера
Задачи для решения на занятии
Решение задач по новому материалу.
Для решения заданий студенту необходимо:
1) знать алгоритм решения СЛУ методом определителей (Крамера);
2) формулировать признаки совместной, несовместной, определенной и неопределенной СЛУ (с помощью определителей);
3) уметь находить значения неизвестных по формулам Крамера;
4) уметь записывать общее решение в случае неопределенной СЛУ.
№2. Решите системы 2-х линейных уравнений с двумя неизвестными методом Крамера (определителей). Обоснуйте, какая СЛУ определенная, несовместная или неопределенная. В случае единственного решения системы выполните проверку.
1)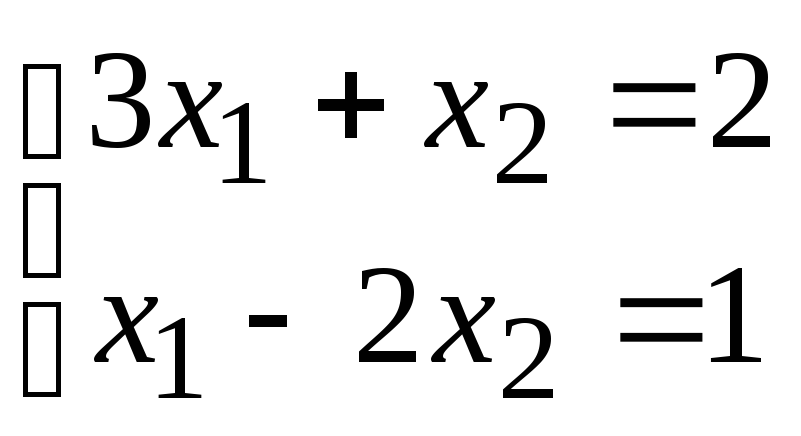 ;
2)
;
2)
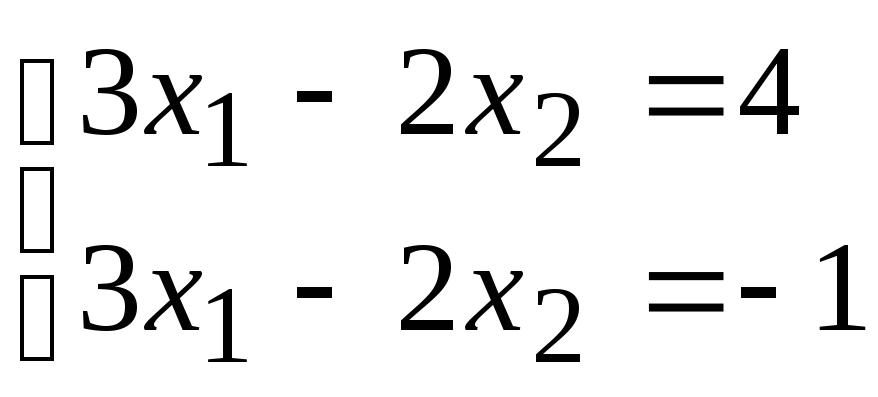 ;
3)
;
3)
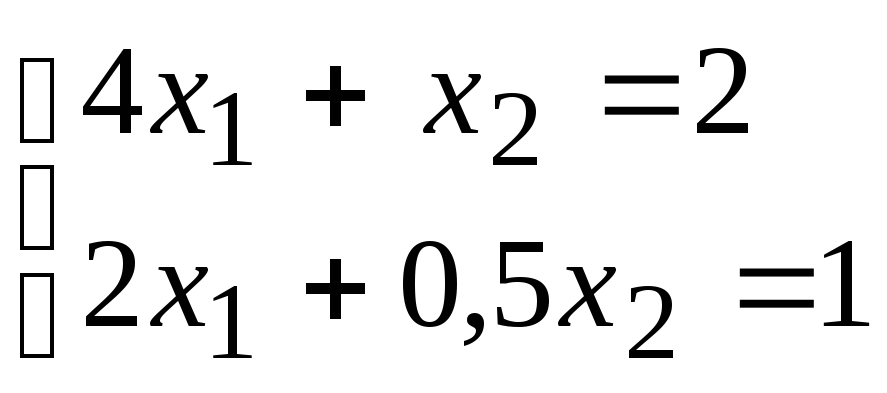 .
.
№3. Решите систему 3-х линейных уравнений с тремя неизвестными методом Крамера (определителей). Обоснуйте, какая СЛУ определенная, несовместная или неопределенная. В случае единственного решения системы выполните проверку.
1)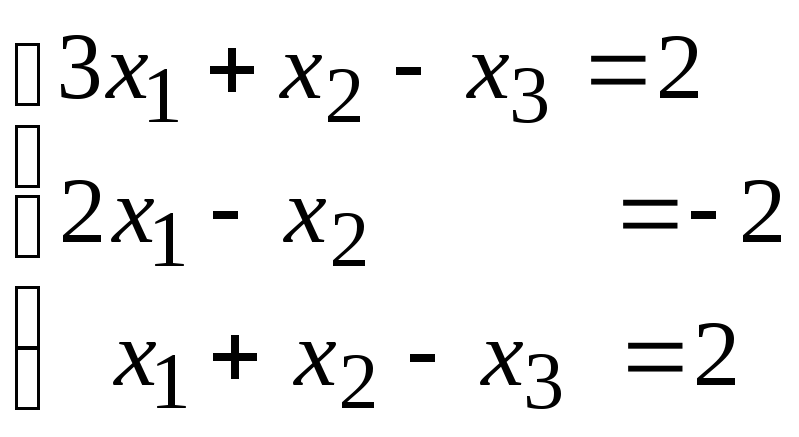 ;
2)
;
2)
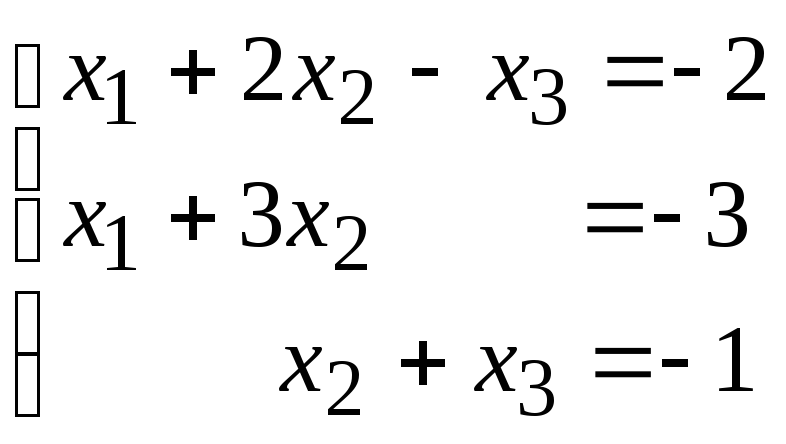 ;
3)
;
3)
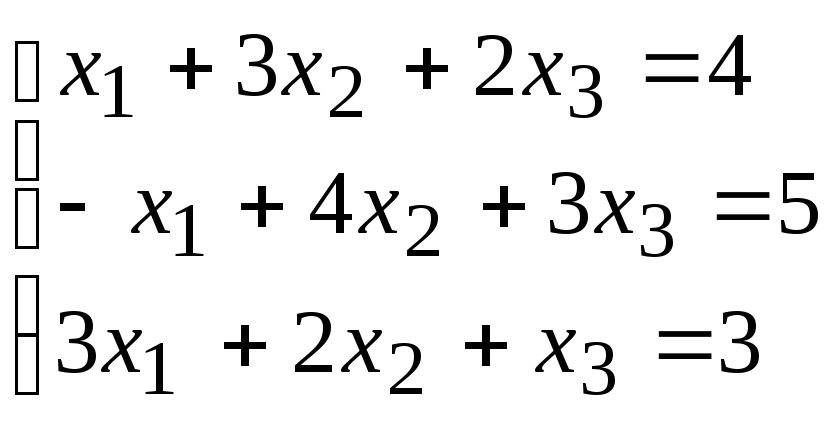 .
.
Задачи для домашнего решения
Закрепление знаний и умений.
№4. Решите систему 2-х линейных уравнений методом Крамера. Обоснуйте, какая СЛУ определенная, несовместная или неопределенная. В случае единственного решения системы выполните проверку.
1)
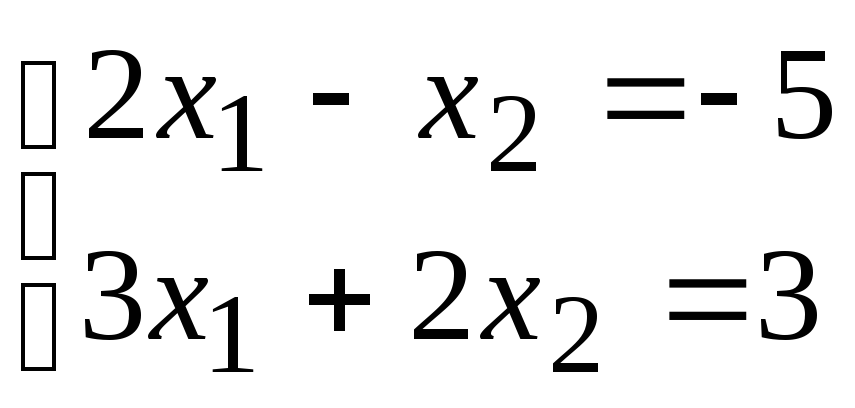 ;
2)
;
2)
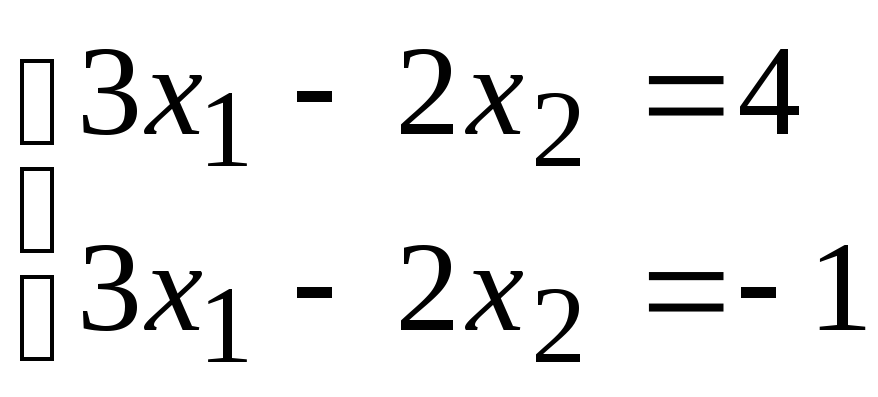 .
.
№5. Решить систему 3-х линейных уравнений методом Крамера. Выполните проверку.
1)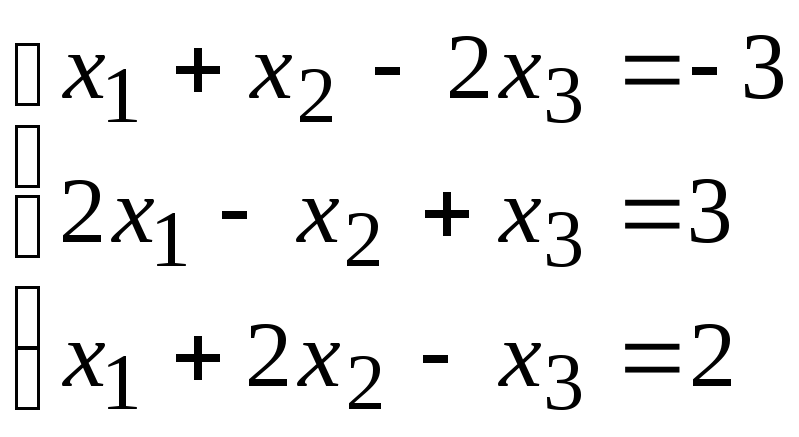 ;
2)
;
2)
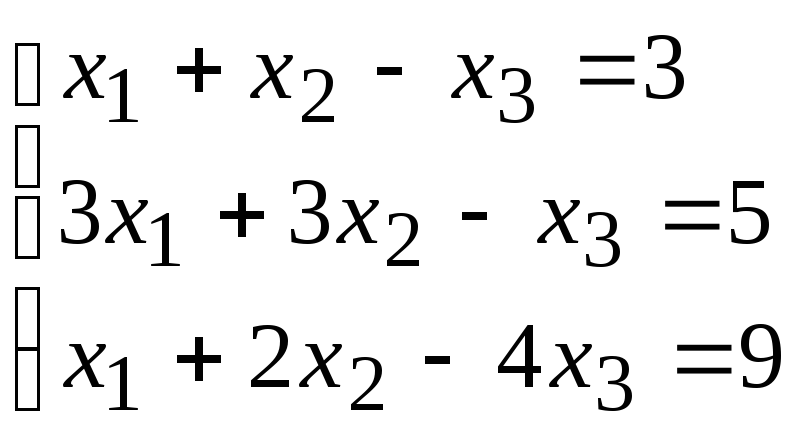 .
.
Ответы.
№2.
1) система
уравнений совместная и определенная,
ее единственное решение
![]() ;
;
2) система несовместная;
3)
система
совместная и неопределенная; общее
решение
![]() ,
,
![]() - любое
действительное число.
- любое
действительное число.
№3.
1)
![]() ;
2) несовместная;
3)
;
2) несовместная;
3)
![]() .
.
№4.
1)
![]() ;
2) несовместная.
;
2) несовместная.
№5.
1)
![]() ;
2)
;
2)
![]() .
.
Практическое занятие 5.
Системы линейных уравнений. Метод исключения неизвестных (гаусса)
Задачи для решения на занятии
Актуализация школьных знаний.
При решении задания №1 повторить понятия: 1) линейное уравнение,
2) система линейных уравнений, 3) решение системы уравнений,
4) несовместная система уравнений, 5) неопределенная система уравнений.
№ 1. Устный опрос.
1)
Какая из данных пар чисел является
решением уравнения
![]() :
:
а) (2; 3); б) (– 2; – 3); в) (2; – 3); г) (– 2; 3).
2)
Является
ли пара чисел
![]() решением
системы уравнений
решением
системы уравнений
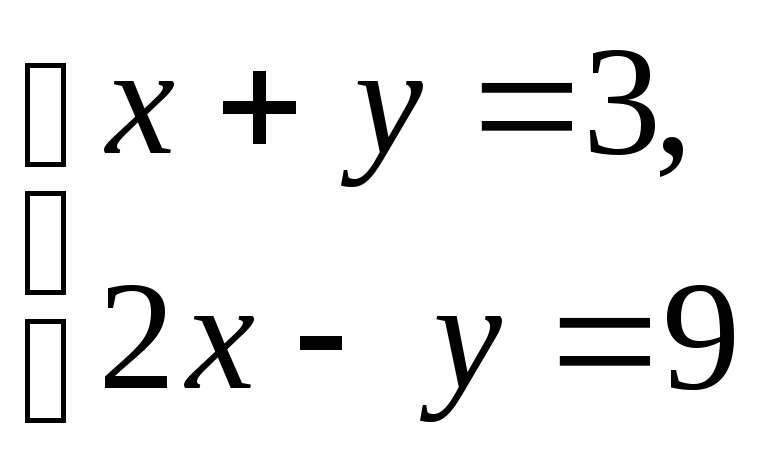 ?
?
3) Имеет ли решения каждая система уравнений и сколько? Ответ обоснуйте.
1)
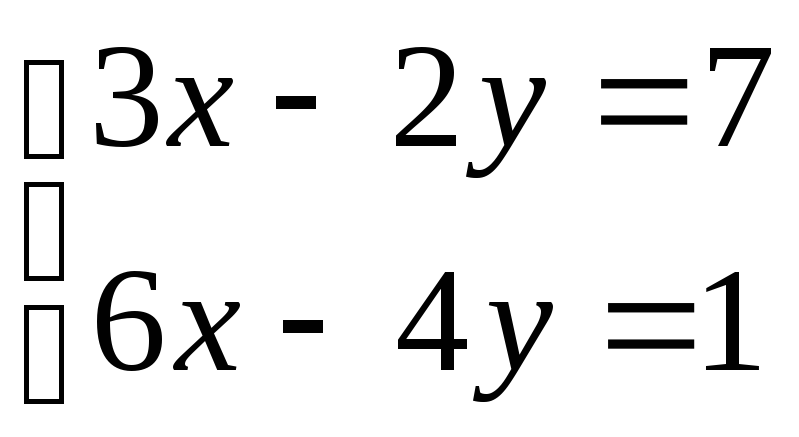 ; 2)
; 2)
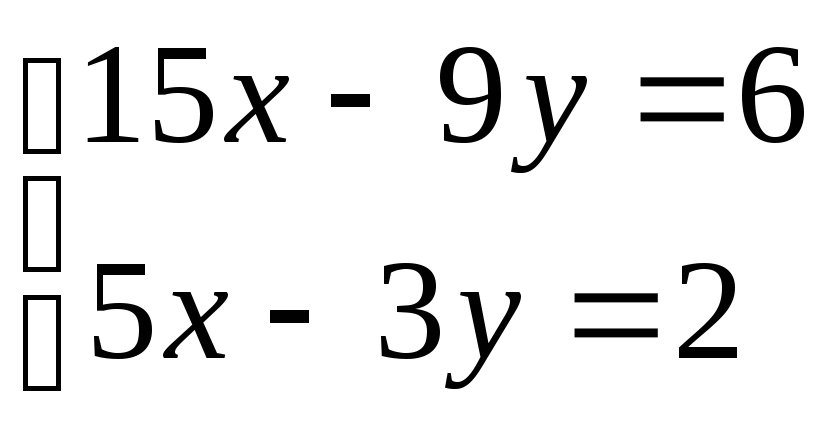 .
.
№2. Решите систему уравнений:
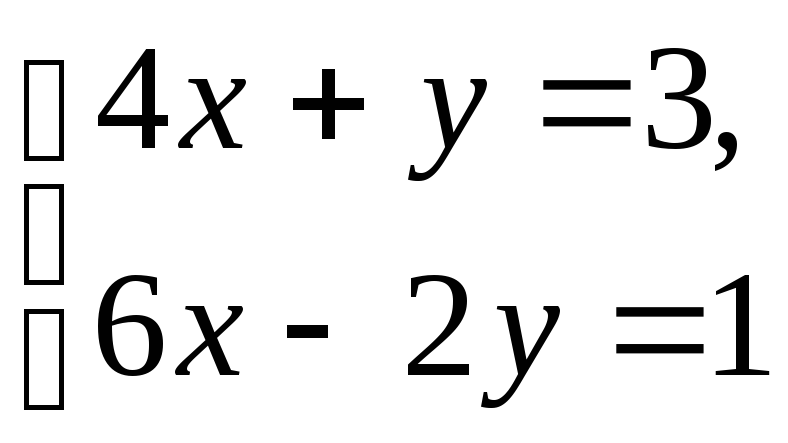 методами:
методами:
а) подстановки; б) алгебраического сложения. Выполните проверку.
Решение задач по новому материалу.
При решении заданий студенту необходимо:
-
знать элементарные преобразования с уравнениями системы,
-
обосновать треугольный вид СЛУ,
-
описать «обратный ход Гаусса» нахождения значений неизвестных,
-
уметь записать общее решение неопределенной системы,
-
знать признаки отсутствия решения СЛУ и бесконечного множества решений СЛУ.
№3. Решить систему 2-х линейных уравнений с двумя неизвестными методом Гаусса (исключения неизвестных), применяя элементарные преобразования над уравнениями.
Записывать
ответ в видах: а) СЛУ совместная и
определенная, решение
![]() ;
б) СЛУ несовместная; в) СЛУ совместная
и неопределенная, общее решение
;
б) СЛУ несовместная; в) СЛУ совместная
и неопределенная, общее решение
![]()
1)
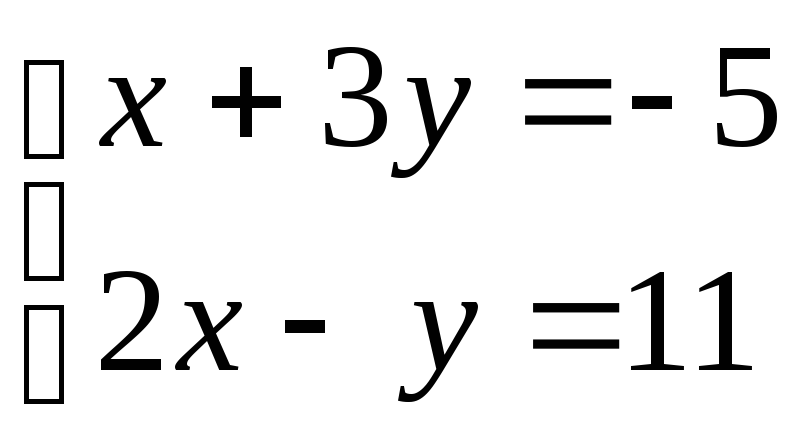 ;
2)
;
2)
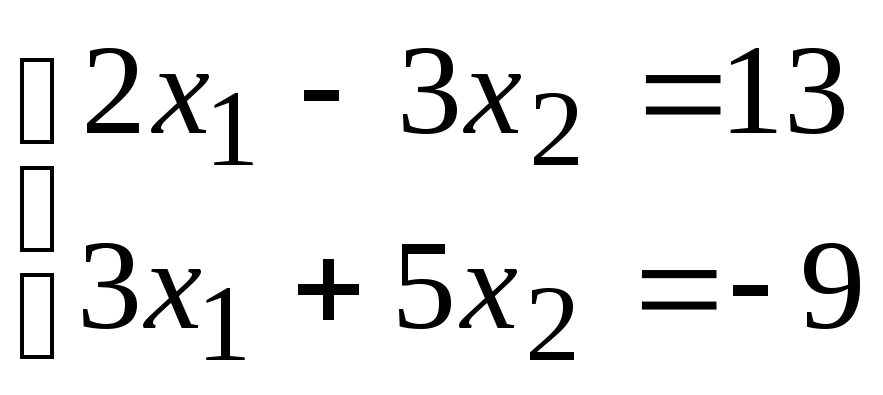 ;
3)
;
3)
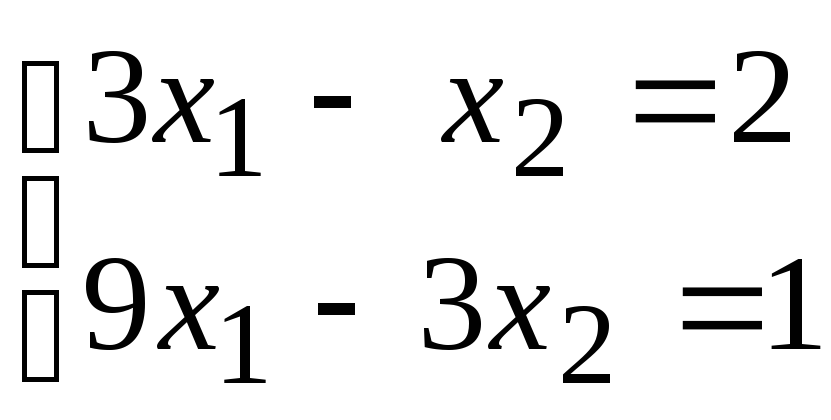 .
.
№4. Решить систему 3-х линейных уравнений методом Гаусса (исключения неизвестных).
Виды
ответа: а) СЛУ совместная и определенная,
решение
![]() ;
б) СЛУ несовместная; в) СЛУ совместная
и неопределенная, общее решение
;
б) СЛУ несовместная; в) СЛУ совместная
и неопределенная, общее решение
![]() .
.
1)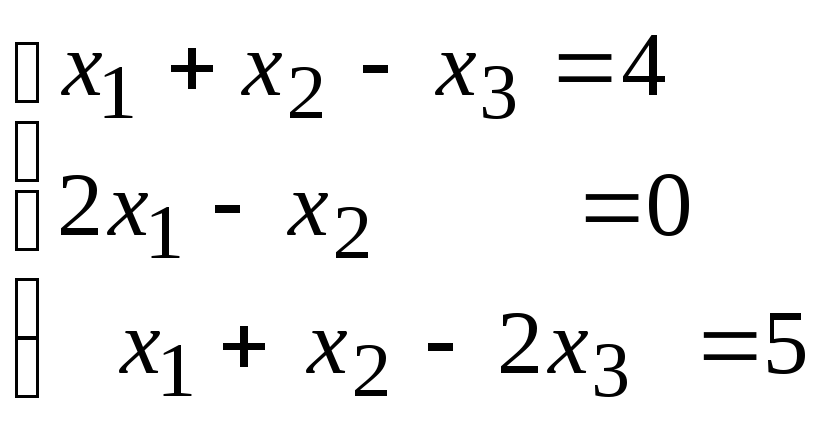 ;
2)
;
2)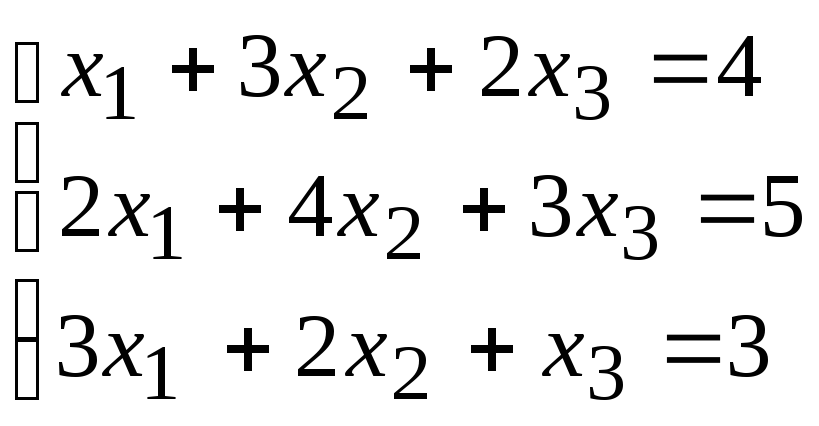 .
.
Задачи для домашнего решения
Закрепление знаний и умений.
№5. Решите систему линейных уравнений методом подстановки или методом алгебраического сложения:
1)
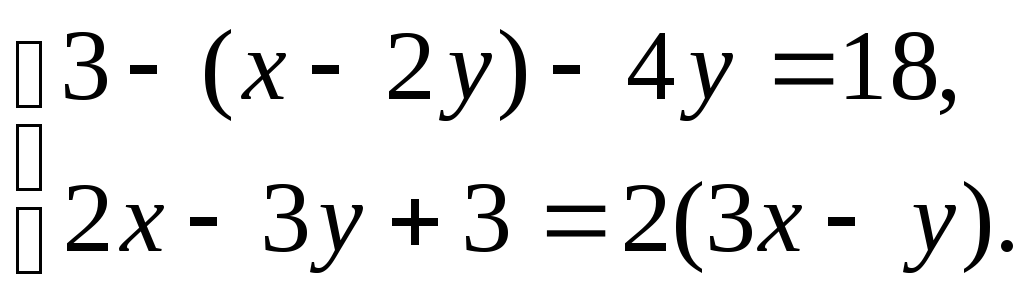 2)
2)
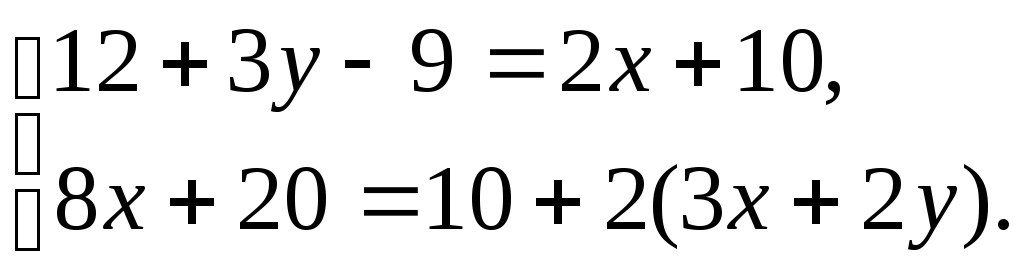
№6. Решить систему двух линейных уравнений методом исключения неизвестных (Гаусса).
1)
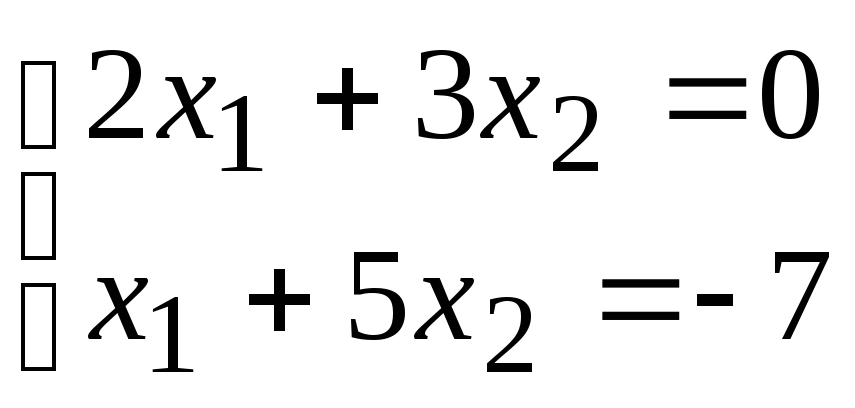 ;
2)
;
2)
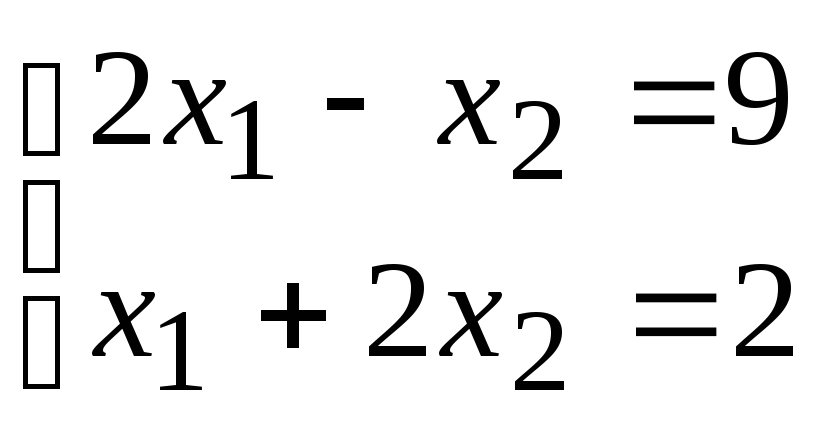 .
.
№7. Решить систему трех линейных уравнений методом Гаусса.
1)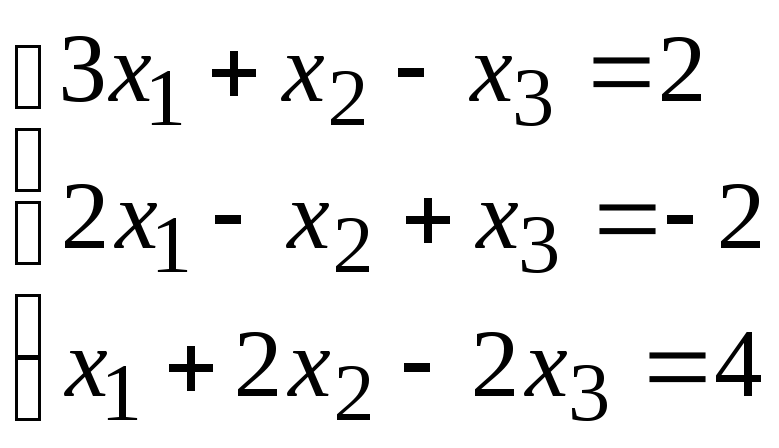 ;
2)
;
2)
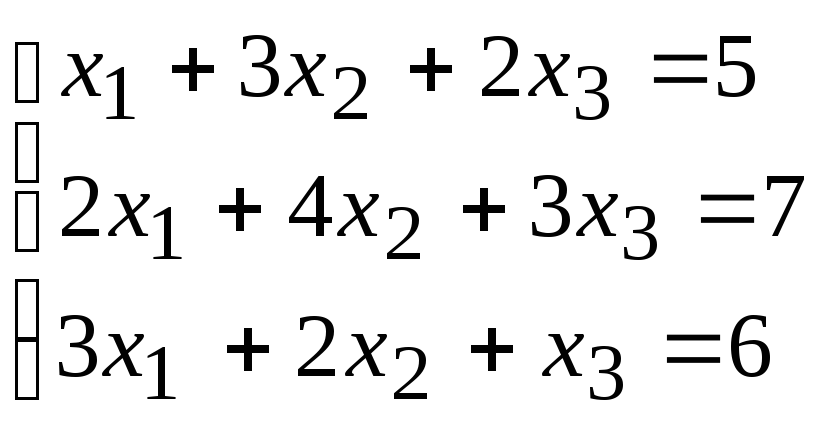 .
.
№8. * Задача с экономическим содержанием
Для
выполнения плана товарооборота
производственно-торговая фирма должна
продать товары в количестве
![]() (тыс. штук) соответственно. Если продавать
эти товары в количествах
(тыс. штук) соответственно. Если продавать
эти товары в количествах
![]() (тыс. штук) соответственно, то план
товарооборота будет перевыполняться
в 1,5 раза. Если продавать в количествах
(тыс. штук) соответственно, то план
товарооборота будет перевыполняться
в 1,5 раза. Если продавать в количествах
![]() соответственно, то выполнение плана
составит 75%.
соответственно, то выполнение плана
составит 75%.
Постройте
математическую модель задачи: составьте
систему линейных уравнений и определите
стоимость единицы товара каждого вида,
если план товарооборота фирмы составляет
![]() тыс. руб.
тыс. руб.
1)
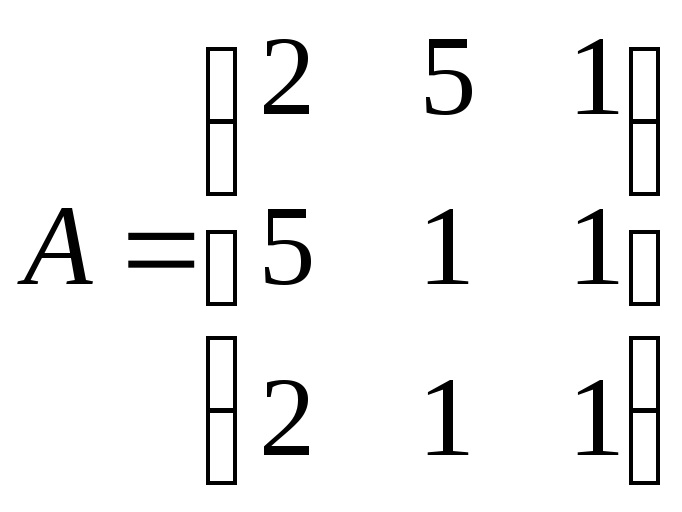 ,
,
![]() ; 2)
; 2)
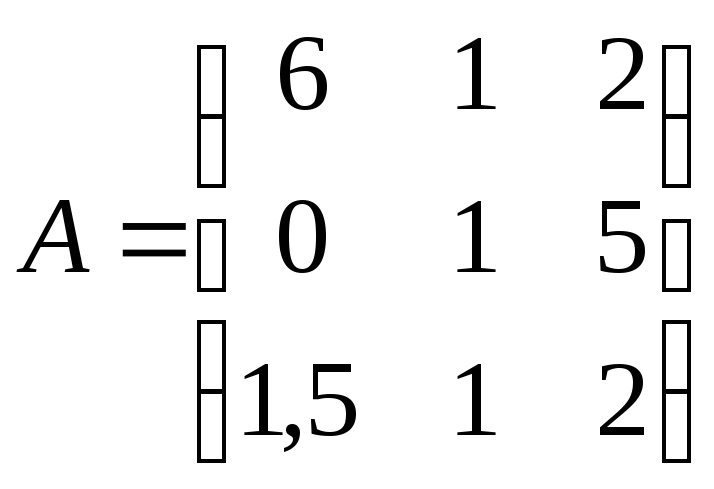 ,
,
![]() ;
;
3)
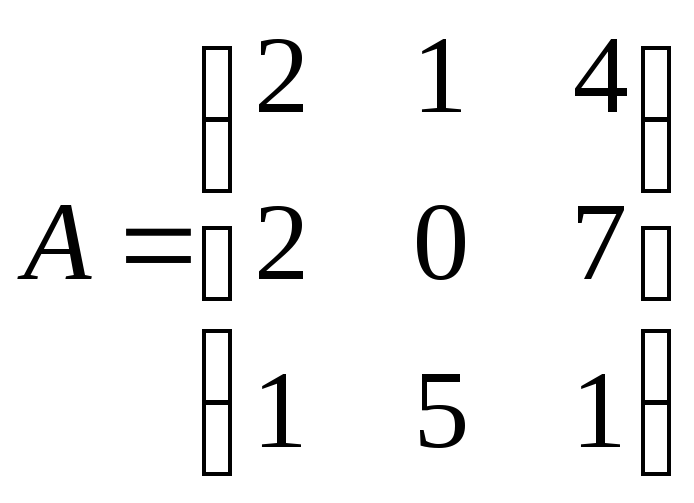 ,
,
![]() ; 4)
; 4)
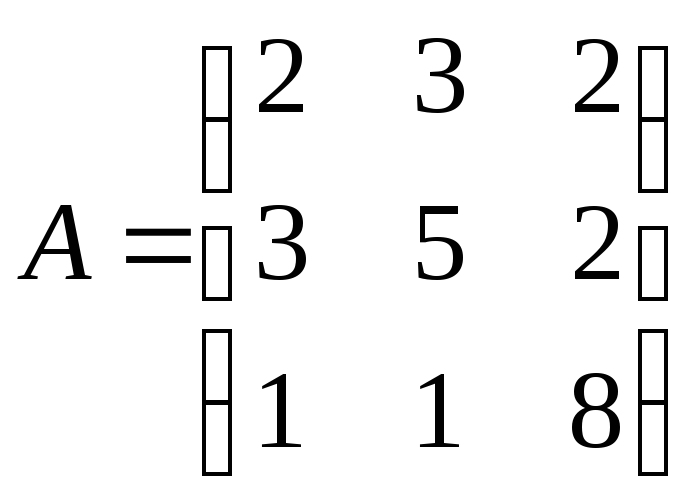 ,
,
![]() .
.
Ответы.
№3.
1)
![]() ;
2)
;
2)
![]() ;
;
3) система несовместная;
№4.
1)
![]() ;
2)
;
2)
![]() .
.
№6.
1)
![]() ;
2)
;
2)
![]() .
.
№7.
1)
![]() ;
2)
;
2)
![]() .
.
Практическое занятие 6.
Контрольная работа № 1 «Линейная алгебра»
Примерный вариант
Задачи на оценку «удовлетворительно»
Задача
1. Даны
матрицы
![]() и
и
![]() ,
число
,
число
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Найти
матрицы: 1)
![]() , 2)
, 2)
![]() .
.
Задача 2. Вычислить определитель по правилу треугольников:
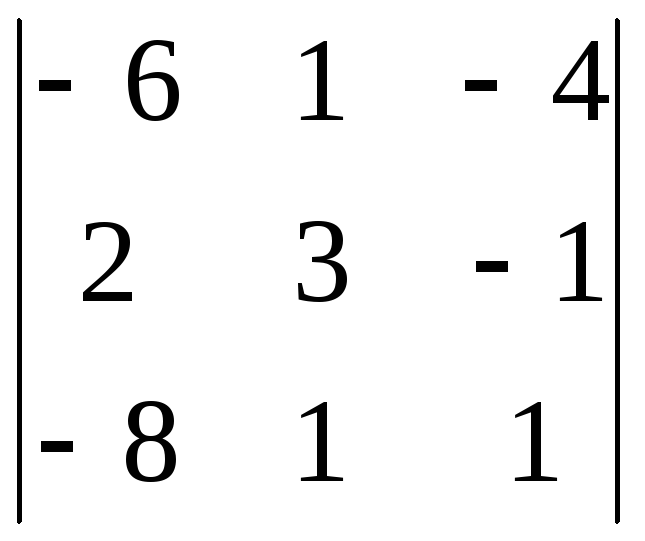 .
.
Задача 3. Решить систему линейных уравнений методом Крамера:
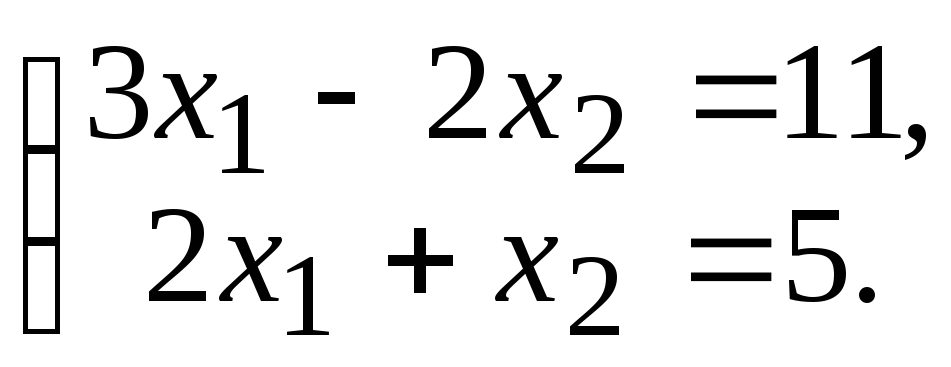 .
.
Задача 4. Решить систему линейных уравнений методом Гаусса:
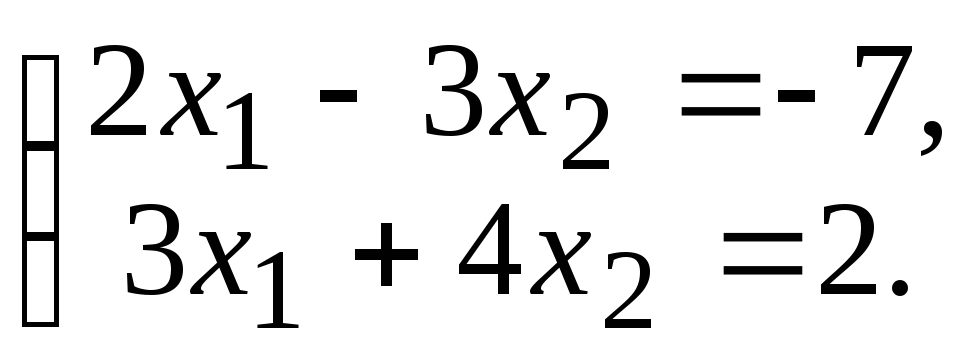
Задачи на оценку «хорошо» и «отлично»
(1-3 задачи на выбор студента)
Задача 5. Решить систему линейных уравнений методом Гаусса (исключения неизвестных):
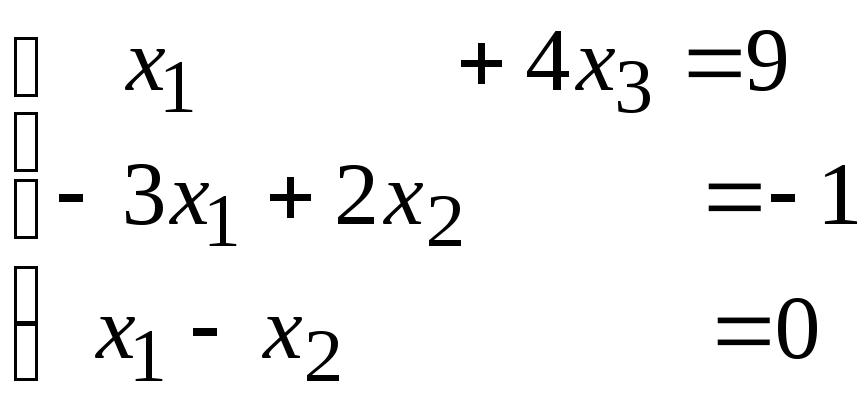 .
.
Задача 6. Вычислить определитель разложением по строке или столбцу:
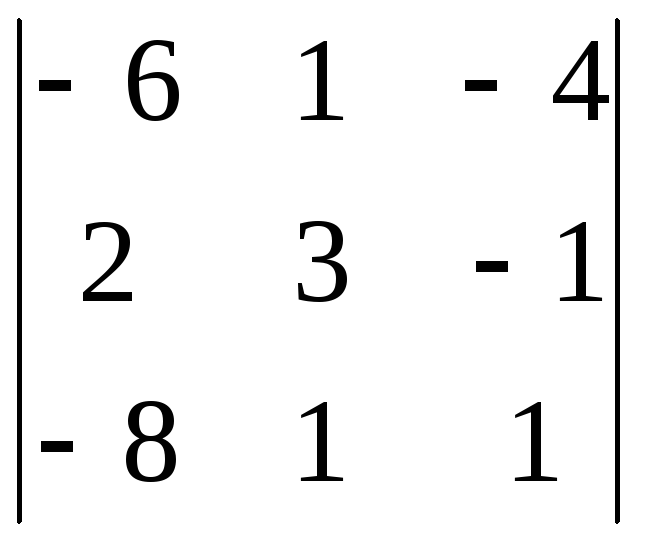 .
.
Задача 7. Найти общее решение системы линейных уравнений и одно из частных решений:
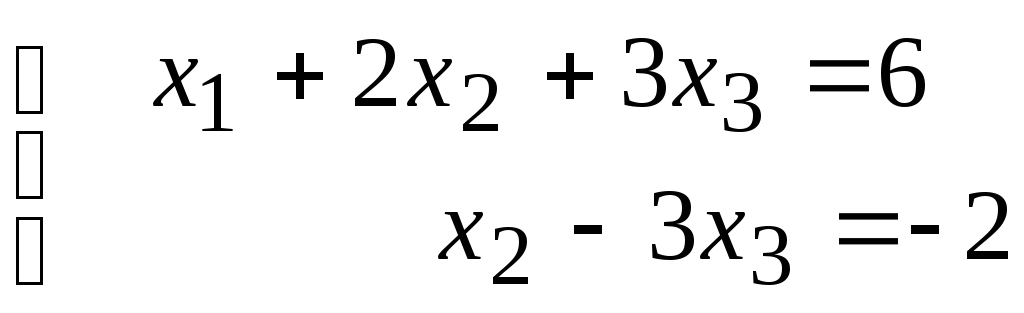 .
.
