Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский государственный технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Тау 5 вариант.doc

Скачиваний:

Добавлен:

04.06.2015

Размер:

3.72 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

3.3 Расчет переходного процесса методом трапеций

Вещественную частотную характеристику (рисунок 10) заменим мало отличающимися от кривой горизонтальными и наклонными прямолинейными участками, образующими с осью ординат трапеции. Действительная ВЧХ при этом будет представлена как алгебраическая сумма трапецеидальных частотных характеристик

, (3.6)

где ‑ число трапеций.

Горизонтальные отрезки чертим в точках экстремумов. Первый отрезок должен начинаться из точки , т.к. эта точка определяет конечное значение переходной характеристики. Более тщательно нужно аппроксимировать начальный участок ВЧХ. Конечный участок с ординатами, меньшими по абсолютному значению, чемможно не принимать во внимание.

Рисунок 11 – Замена вещественной частотной характеристики трапециями.

Полученные трапеции вычертим на другом чертеже (рисунок 12) таким образом, чтобы основание каждой из них легло на ось .

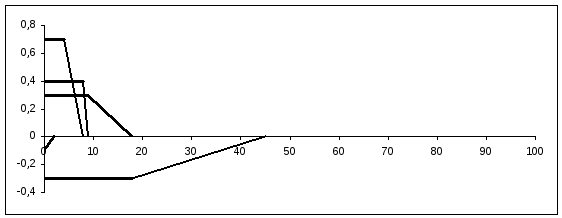
Рисунок 12 – Трапеции вещественной частотной характеристики.

Определим параметры трапеций.

Из графиков находим

По значениям вычислим коэффициенты наклона

(3.7)

и округлим их до ближайшего из значений 0; 0,05; 0,1; 0,15; … 0,95; 1.

Подставив численные значения, получим

Рассчитаем переходные процессы отдельно для каждой трапеции.

В таблице h-функций таблица 4.2 с.222 [3] для каждой i-й трапеции отыскивается столбец, соответствующий значению коэффициента наклона . Затем для ряда значений условного временивыписывают соответствующие им значения. По значениямивычисляют значения действительного времении составляющей переходной характеристики:

; . (3.8)

Результаты оформим в таблице 5.

Таблица 5 – Расчет графиков составляющих переходной характеристики

Трапеция 1				Трапеция 2				Трапеция 3
n=2 Р=-0.1 =0				n=45 Р=-0.3 =0,5				n=8 Р=0.7 =0,5
t				t				t			
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											
											

Продолжение таблицы 5

Трапеция 4				Трапеция 5
n=9 Р=0.4=0,9				n=18Р=0.3=0,5
t				t			
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							
							

Далее построим графики составляющих переходной характеристики . Все составляющие расположим на одном чертеже (рисунок 12) с учетом знака, который определяется знаком высотысоответствующей трапеции.

График переходной характеристики замкнутой системы получим путем суммирования ординат всех составляющих в равные моменты времени

. (3.9)

Рисунок 13 – График переходного процесса и его составляющие.

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.2025693.25 Кб0сэп.doc
#
15.08.20191.72 Mб4Т.Н.Баринова Иформатика Часть 1. Создание текст...doc
#
04.06.20153.9 Mб91Тайны восприятия. Г. Хакен, М. Хакен-Крелль.pdf
#
04.06.201514.3 Mб18ТАКСАЦИОННЫЕ ОПИСАНИЯ РУДИКОВСКОЕ УЧ.Л-ВО.doc
#
27.03.20161.65 Mб19таксация.rtf
#
04.06.20153.72 Mб65Тау 5 вариант.doc
#
04.06.20153.9 Mб50ТАУ7 распечатать.doc
#
04.06.20151.47 Mб40ТАУКурсак(Андрей).doc
#
26.08.2019483.45 Кб90ТБУ задачи к практич занятиям.docx
#
01.08.2019755.52 Кб7ТВП.docx
#
04.06.201518.36 Кб18Текст, ноксология.docx