1.4 Исследование системы на устойчивость по критерию Найквиста

Определим устойчивость разомкнутой системы.

В одноконтурной системе, составленной из последовательно соединенных звеньев, корни характеристических полиномов этих звеньев являются одновременно корнями характеристического полинома разомкнутой системы. Так как система не содержит местных обратных связей, определим корни характеристических полиномов звеньев.

Характеристический полином звена :

(1.16)

имеет вещественные корни:

= -2

р₂=-1,16

р₃=-12,728

Характеристический полином звена :

(1.17)

имеет три корня: два комплексных сопряженных и один нулевой

р₄= -15,38.

Так как все корни имеют отрицательное значение - разомкнутая система устойчива.

Передаточная функция разомкнутой системы имеет вид:

(1.18)

Составим частотную передаточную функцию:

(1.19)

где:

Запишем вещественную и мнимую части частотной передаточной функции:

(1.20)

Подсчитаем значения мнимой и действительной части частотной передаточной функции для различных значений от 0 до. Результаты вычислений оформим в виде таблицы 2.

Таблица 2 – Расчет АФЧХ разомкнутой системы

ω	U1	V1	U2	V2	U(ω)	V(ω)
0,1	4051	0	0,99369022	0,1504312	467,503278	-70,773645
1	4051	0	0,3712	1,4362	80,1624431	-310,15437
2	4051	0	-1,4888	2,4596	-85,587258	-141,39604
3	4051	0	-4,5008	2,6574	-78,289179	-46,224152
4	4051	0	-8,5328	1,6168	-53,760812	-10,18663
5	4051	0	-13,4	-1,075	-35,235913	2,82676166
6	4051	0	-18,8648	-5,8308	-22,993172	7,10681215
7	4051	0	-24,6368	-13,0634	-15,055351	7,98293908
8	4051	0	-30,3728	-23,1856	-9,8851872	7,54602793
9	4051	0	-35,6768	-36,6102	-6,4878308	6,6575697
10	4051	0	-40,1	-53,75	-4,2373166	5,67969496
20	4051	0	100,6	-520,3	0,17022648	0,88040595
30	4051	0	1215,1	-1812,45	0,12126902	0,18088555
40	4051	0	4623,4	-4343	0,05460183	0,05129033
50	4051	0	12173,5	-8524,75	0,02619172	0,01834131
60	4051	0	26241,4	-14770,5	0,01375188	0,00774052
70	4051	0	49731,1	-23493,05	0,00781203	0,00369042
80	4051	0	86074,6	-35105,2	0,00473344	0,00193052
90	4051	0	139231,9	-50019,75	0,00302287	0,00108598
∞	4051	0	∞	∞	0	0

По данным таблицы 2 построим график АФЧХ разомкнутой системы (рисунок 7).

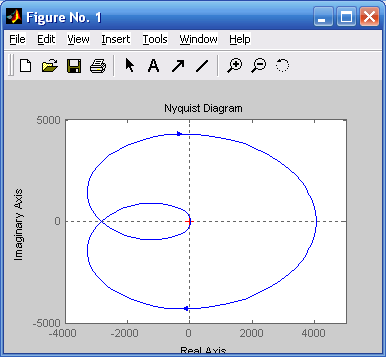
Рисунок 7 – АФЧХ разомкнутой системы

Так как характеристический полином системы не имеет положительных корней, то система является устойчивой. Согласно условию устойчивости по критерию Найквиста, в этом случае для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до ∞, дополненная на участке разрыва дугой бесконечного радиуса, не охватывала точку с координатами (-1,j0).

Для данной системы это условие не выполняется, АФЧХ разомкнутой системы один раз охватывает точку с координатами (-1,j0), следовательно, система не устойчива.