1 Анализ линейной системы автоматического регулирования

1.1 Преобразование структурной схемы и определение передаточных функций системы

Приведем заданную структурную схему к одноконтурной с помощью последовательных преобразований (рисунок 2).

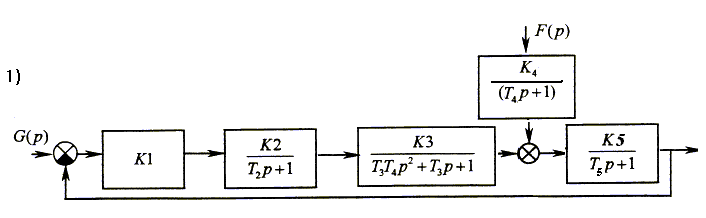
Рисунок 2 – Преобразование исходной структурной схемы

Где:

‑передаточные функции элементов прямой цепи;

‑входной и выходной сигналы соответственно.

Передаточные функции элементов прямой цепи:

; (1.1)

Передаточная функция возмущающего воздействия:

(1.2)

Передаточная функция разомкнутой системы:

(1.3)

(1.4)

где ‑ общий коэффициент усиления,

‑коэффициенты собственного оператора.

Подставив численные значения, получим:

. (1.5)

Исходя из структурной схемы видно, что система охвачена единичной обратной связью. Передаточная функция замкнутой системы по задающему воздействию:

(1.6)

Подставив численные значения, получим:

(1.7)

Характеристическое уравнение замкнутой АСР получают путем выделения знаменателя ее передаточной функции и приравнивая его к нулю.

(1.8)

1.2 Исследование системы на устойчивость по критерию Гурвица

Передаточная функция замкнутой системы:

(1.9)

Тогда характеристическое уравнение:

(1.10)

Найдем главный определитель Гурвица и определители низших порядков:

.

Подставив численные значения, получим:

Δ1 =	0,000565
Δ2 =	0,0000000005162
Δ3 =	-0,001292
Δ4 =	-5,236

Для устойчивости системы необходимо и достаточно, чтобы определитель Гурвица и все его диагональные миноры при а₀>0 были положительны, т.е. Δ₁> 0, Δ₂> 0, Δ₃> 0, … , Δ_n> 0.

Условие Гурвица не выполняется для данной системы, следовательно, делаем вывод, что система не устойчива.

Найдем критический коэффициент усиления для данной системы из условия:

, (1.11)

подставляя численные значения, получим:

Kкр=1,425

1.3 Исследование системы на устойчивость по критерию Михайлова

Для оценки устойчивости по критерию Михайлова необходимо построить кривую, которую описывает конец вектора на комплексной плоскости при изменении частотыот 0 до, называемую годографом Михайлова.

Вектор получают из характеристического полинома замкнутой системы при подстановке:

(1.12)

Данное выражение представим в виде:

(1.13)

где и, – вещественная и мнимая частисоответственно

(1.14)

Подставляя численные значения, получим

. (1.15)

Задавая значения от 0 до, вычисляеми. Расчет оформляем в виде таблицы 1.

Таблица 1 – Координаты годографа Михайлова

ω	0	5	10	15	20	25	30	35	40	45	50
Х(ω)	476,2	461,8	435,1	445,6	575,8	941,2	1690,3	3004,6	5098,6	8219,8	12648,7
Y(ω)	0	-3,6	-58,8	-217,2	-530,4	-1050	-1827,6	-2914,8	-4363,2	-6224,4	-8550

По данным таблицы 1 строим годограф Михайлова (рисунок 6).

Рисунок 6 ‑ Годограф Михайлова

Для устойчивости системы необходимо, чтобы годограф Михайлова обошел в положительном направлении (против часовой стрелки) последовательно квадрантов (гдепорядок характеристического уравнения), нигде не обращаясь в нуль. Если это условие не выполняется, система не устойчива. Для данной системы условие устойчивости Михайлова не выполняется. Система неустойчива.