4. Диполь и расчёт поля диполя.

Электрический Диполь – это система состоящая из двух одинаковых по величине, но противоположных зарядов, находящихся на малом расстоянии друг от друга по сравнению с расстоянием до других точек электрического поля. Вектор L проведённый от – к +, по модулю равный расстоянию между зарядами называется плечом Диполя.

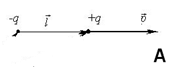
1 Напряжённость поля Диполя в точке А на оси Диполя

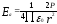
2. Напряжённость поля в точке В на перпендикуляре восстановленном к середине Диполя

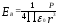
Видно, что поле на оси Диполя в 2 раза больше поля на перпендикуляре.

5. Поток вектора напряжённости. Теорема Остроградского-Гаусса для электростатических полей в вакууме.

поток вектора напряженности электрического поля равен числу линий напряженности, пересекающих поверхность S.

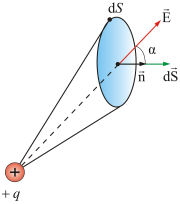Для данной конфигурации поток вектора напряженности через произвольную элементарную площадку dS будет равен:

В каждой точке поверхности S₁ проекция  на направление внешней нормали одинакова и равна:  тогда поток через S₁ Подсчитаем поток через сферу S₂, имеющую радиус R₂:Из непрерывности линииследует, что поток и черезлюбую произвольную поверхность S будет равен этой же величине:

теорема Гаусса для одного заряда.Полученный результат справедлив не только для одного заряда, но и для любого числа произвольно расположенных зарядов, находящихся внутри поверхности:

   –теорема Гаусса для нескольких зарядов 

  

6. Поле бесконечной заряжённой плоскости, двух разноимённо заряжённых плоскостей, заряжённой сферы.

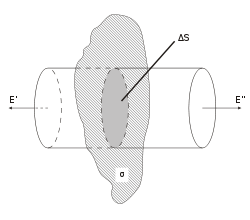
              Рассмотрим поле, создаваемое бесконечной однородно заряженной плоскостью с везде одинаковой поверхностной плотностью заряда . Представим себе мысленно цилиндр с образующими, перпендикулярными к заряженной плоскости, и основаниями (площадью каждое), расположенными относительно плоскости симметрично.

Линии напряжённости паралельны боковым её сторонам т.е не пронизывают их т.е поток через них равен 0.

Таким образом линии пронизывают стороны основнаний и получим:

Напряжённость бесконечной плоскости определяется:

Поле заряжённой сферы радиусом R

При выборе в качестве замкнутой поверхности сферы радиусом R, напряжённость вычисляется аналогично:

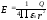
7. Поле равномерно заряженного шара, Поле бесконечно заяженного цилиндра(нити)

Шар:

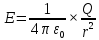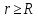
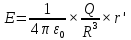, при

при

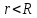
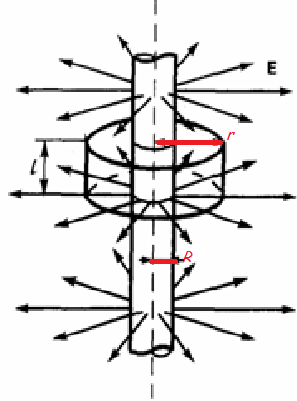
Поле бесконечно прямой равномерно заряженной нити с :

/

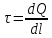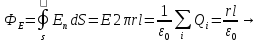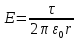, при r>R

8.Работа электростатического поля:

Пусть электростатическое поле образованно зарядом Q>0. Пусть в этом поле по произвольной траектории перемещается другой точечный положительный заряд Q₀ из точки 1 в 2.

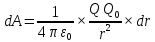
Полная работа совершаемая полем на всем участке пути:

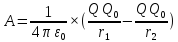
Значение работы зависит от положения начальной и конечной точек пути. Таким образом электростатические поля являются потенциальными, а кулоновские силы – консервативными.

Работа совершаемая позамкнотому контуру пути будет равна 0, т.е.:

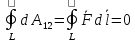
9. Циркуляция вектора напряженности электростатического поля

Если в качестве заряда Q₀, которого перемещают в электростатическом поле, взять единичный точечный положительный заряд, то произведение 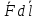будет численно равно 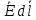, тогда:  (3)  Интеграл называется циркуляцией вектора напряженности. Значит, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, которое обладает свойством (3), называетсяпотенциальным. Из равенства нулю циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они обязательно начинаются на положительных зарядах, а заканчиваются на отрицательных.