Энергетическая интерпретация уравнения Бернулли:

- удельная энергия положения;

- удельная энергия давления;

- удельная потенциальная энергия;

- удельная кинетическая энергия;

- полная удельная энергия;

-потери полной удельной энергии.

Слово «удельная » в энергетической интерпретации означает, что каждый член уравнения Бернулли отнесен к единице веса жидкости, проходящей через живое сечение в единицу времени.

Уравнение Бернулли может быть применено к потоку, только при выполнении трех условий:

1. Расход жидкости между двумя сечениями 1-1 и 2-2, из которых первое всегда располагается выше по течению, должен быть постоянным (Q=const).

2. Движение жидкости должно быть установившемся.

3. Движение жидкости в сечениях 1-1 и 2-2 должно быть параллельноструйным или плавноизменяющимся; в промежутке между выбранными сечениями движение может быть и резко изменяющимся.

В уравнении (3.3) коэффициент кинетической энергии (коэффициент Кориолиса) равен отношению действительной кинетической энергии потока, имеющего в живом сечении эпюру распределения скоростей, к кинетической энергии, вычисленной по средней скорости в живом сечении. По опытным данным при турбулентном прямолинейном движении воды в трубах.

Удельная энергия потока (гидродинамический напор) при движении реальной жидкости уменьшается в направлении движения от первого сечения ко второму. Поэтому, откладывая каждый раз (в расчетных сечениях по длине) от горизонтальной плоскости 0-0 величинув сечениях, получим напорную линию, уклон которой на прямолинейных участках трубопровода есть гидравлический уклон:

. (3.4)

Ниже линии на расстоянии от плоскости сравнения равном(или от линии на расстоянии) располагается пьезометрическая линия , уклон которой называется пьезометрическим

, (3.5)

причем величина уклона может быть 0>>0, а в частном случае и равна нулю.

Если при построении пьезометрическая линия на некотором участке располагается ниже оси трубопровода, то это значит, что на участке давление меньше атмосферного, т.е. наблюдается вакуум. Разность между ординатами рассматриваемой точки сечения и пьезометрической линии на данной вертикали соответствует величине вакуума , выраженного вводяного столба.

В зависимости от положения уровня воды на выходе различают свободное и затопленное истечение из коротких трубопроводов. При свободном незатопленном истечении местные потери напора на выходе потока из грубы будут равны нулю, а пьезометрическая линия приходит к центру выходного сечения. При затопленном истечении потери напора на выход имеют место и определяются как на внезапное расширение, а линияприходит к отметке уровня воды на выходе.

Кроме уравнения Бернулли, к основным, которые используются при расчете коротких трубопроводов, относятся и другие зависимости, в том числе основное уравнение расхода, уравнение неразрывности, формулы Вейсбаха и Дарси - Вейсбаха.

Основное уравнение для расхода

, (3.6)

откуда

, (3.7)

где - площадь живого сечения;

- средняя скорость в живом сечении.

Уравнение неразрывности или баланса расхода:

. (3.8)

Потери напора по длине, обусловленные вязкостью жидкости и шероховатостью поверхности труб, вычисляются по формуле Дарси-Вейсбаха:

, (3.9)

где - коэффициент гидравлического трения или коэффициент Дарси.

Исследованиями зависимости коэффициента , выполненными Никурадзе (рисунок 2.1) и др., установлены тризоны сопротивлений - зона ламинарного, переходного и турбулентного режима. Зона турбулентного режима, в свою очередь, подразделяется на три области - область гидравлически гладких русел (труб), доквадратичная и квадратичная области сопротивлений.

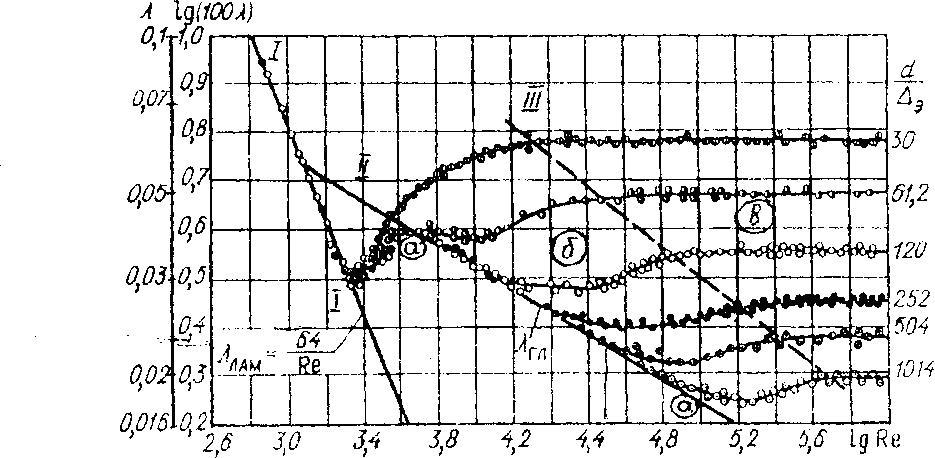
Рисунок 3.1 - График Никурадзе для труб с однородной равнозернистой шероховатостью