
- •Министерство образования и науки
- •Задание к выполнению
- •Методические основы расчета
- •1. Гидростатика и гидродинамика
- •2. Давление воды на плоские поверхности
- •3. Гидравлический расчет коротких трубопроводов
- •Геометрическая интерпретация уравнения Бернулли:
- •Энергетическая интерпретация уравнения Бернулли:
- •I - Зона ламинарного режима; II - Зона переходного режима; III - Зона турбулентного режима;
- •Варианты индивидуального домашнего задания
- •Задачи по вариантам
- •Библиографический список
- •Приложения
Министерство образования и науки
Российской Федерации
Федеральное государственное бюджетное
образовательное учреждение
высшего профессионального образования
Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ
А.В. Самойленко
Методические указания
к индивидуальному домашнему заданию по дисциплине
«МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ»
Волгодонск 2012 г.
СОДЕРЖАНИЕ
Задание к выполнению……………………………………………………........3
Методические основы расчета………………………………………………...3
1. Гидростатика и гидродинамика …............................................................…....3
2. Давление воды на плоские поверхности.........................................................3
3. Гидравлический расчет коротких трубопроводов.........................................11
Варианты индивидуального домашнего задания..................………...........22
Задачи по вариантам………………………………………………………......22
Библиографический список………………………………………………......33
Приложения…………………………………………………………………......34
Задание к выполнению
Задание состоит из:
- перечня необходимых расчетных величин;
- вариантов задания, приведенных на стр. 22;
- необходимых справочных величин, приведенных в приложении.
Представленный объем материала и его построение позволяет использовать методические указания как для аудиторной, так и для самостоятельной работы студентов.
Методические основы расчета
1. Гидростатика и гидродинамика
Гидроста́тика - раздел физики сплошных сред, изучающий равновесие жидкостей, в частности, в поле тяжести.
Основной
закон гидростатики для толщи жидкости
- зависимость давления от глубины,
который для несжимаемой жидкости в
однородном поле тяжести имеет вид
![]() .
Из этого закона следует равенство
уровней в сообщающихся сосудах, закон
Архимеда.
.
Из этого закона следует равенство
уровней в сообщающихся сосудах, закон
Архимеда.
Форма свободной поверхности жидкости определяется комбинацией внешних сил (прежде всего, сил тяготения) и сил поверхностного натяжения. Для больших масс жидкости преобладают силы тяготения и свободная поверхность принимает форму эквипотенциальной поверхности, а при размерах порядка или меньше сантиметра (для пресной воды) определяющими являются капиллярные силы.
Гидродина́мика - раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа. Как и в других разделах физики сплошных сред, прежде всего осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения.
При выполнении задания раздела гидростатика и гидродинамика студент должен использовать курс лекций, практических занятий и учебник [6].
2. Давление воды на плоские поверхности
Гидростатическое
давление в точке есть предел отношения
силы давления
![]() к элементарной площадке бесконечно
малых размеров
к элементарной площадке бесконечно
малых размеров![]() :
:
![]() . (2.1)
. (2.1)
Гидростатическое давление обладает двумя свойствами:
1. Гидростатическое давление действует всегда нормально к площади, воспринимающей давление жидкости, и является сжимающим.
2. Величина гидростатического давления в любой точке не зависит от ориентировки (угла наклона) площадки, а зависит от местоположения точки (глубины ее погружения).
Предел
в виде зависимости (2.1) выражает модуль
(значение) напряжения
![]() .
Поэтому иногда отмечается, что
гидростатическое давление в точке есть
скалярная величина, равная модулю
напряжения.
.
Поэтому иногда отмечается, что
гидростатическое давление в точке есть
скалярная величина, равная модулю
напряжения.
Для
любой точки покоящейся жидкости,
находящейся на глубине
![]() ,
величина абсолютного (полного)
гидростатического давления определяется
как сумма поверхностного и весового
давления
,
величина абсолютного (полного)
гидростатического давления определяется
как сумма поверхностного и весового
давления
![]() , (2.2)
, (2.2)
где ![]() ,
,![]() ,
,![]() - абсолютное, поверхностное и весовое
давления;
- абсолютное, поверхностное и весовое
давления;
![]() =1000
кг/м3
- плотность жидкости (воды);
=1000
кг/м3
- плотность жидкости (воды);
![]() =9,81
м/с2
- ускорение свободного падения.
=9,81
м/с2
- ускорение свободного падения.
Если
абсолютное давление
![]() в точке превышает величину атмосферного
давления, то превышение абсолютного
давления над атмосферным называется
избыточным или манометрическим давлением:
в точке превышает величину атмосферного
давления, то превышение абсолютного
давления над атмосферным называется
избыточным или манометрическим давлением:
![]() . (2.3)
. (2.3)
На
практике давление на свободной поверхности
воды
![]() ,
как правило, равно атмосферному, т.е.
,
как правило, равно атмосферному, т.е.![]() .
В этих случаях
.
В этих случаях![]() ,
которое в дальнейшем будем обозначать
через
,
которое в дальнейшем будем обозначать
через![]() ,
из формулы (2.3) будет равно:
,
из формулы (2.3) будет равно:
![]() , (2.4)
, (2.4)
т.е. избыточное гидростатическое давление в точке равняется весовому давлению.
Сила абсолютного гидростатического давления, действующая на плоскую поверхность, равна сумме:
![]() , (2.5)
, (2.5)
где ![]() - сила поверхностного давления;
- сила поверхностного давления;
![]() - сила избыточного (весового)
гидростатического давления;
- сила избыточного (весового)
гидростатического давления;
![]() - площадь смоченной плоской поверхности;
- площадь смоченной плоской поверхности;
![]() - глубина погружения центра тяжести
смоченной поверхности.
- глубина погружения центра тяжести
смоченной поверхности.
При
расчетах силы давления воды на плоские
поверхности, например, на
![]() ,
как показано на рисунке 2.1, поверхностное
давление
,
как показано на рисунке 2.1, поверхностное
давление![]() ,
передаваясь всем точкам внутри покоящейся
жидкости без изменения величины (закон
Паскаля), уравновешивается таким же
поверхностным (атмосферным) давлением
с другой стороны поверхности
,
передаваясь всем точкам внутри покоящейся
жидкости без изменения величины (закон
Паскаля), уравновешивается таким же
поверхностным (атмосферным) давлением
с другой стороны поверхности![]() .
Поэтому в для большинства случаев, когда
.
Поэтому в для большинства случаев, когда![]() ,
определяется только сила избыточного
гидростатического давления:
,
определяется только сила избыточного
гидростатического давления:
![]() , (2.6)
, (2.6)
где ![]() - избыточное гидростатическое давление
в центре тяжести площади.
- избыточное гидростатическое давление
в центре тяжести площади.
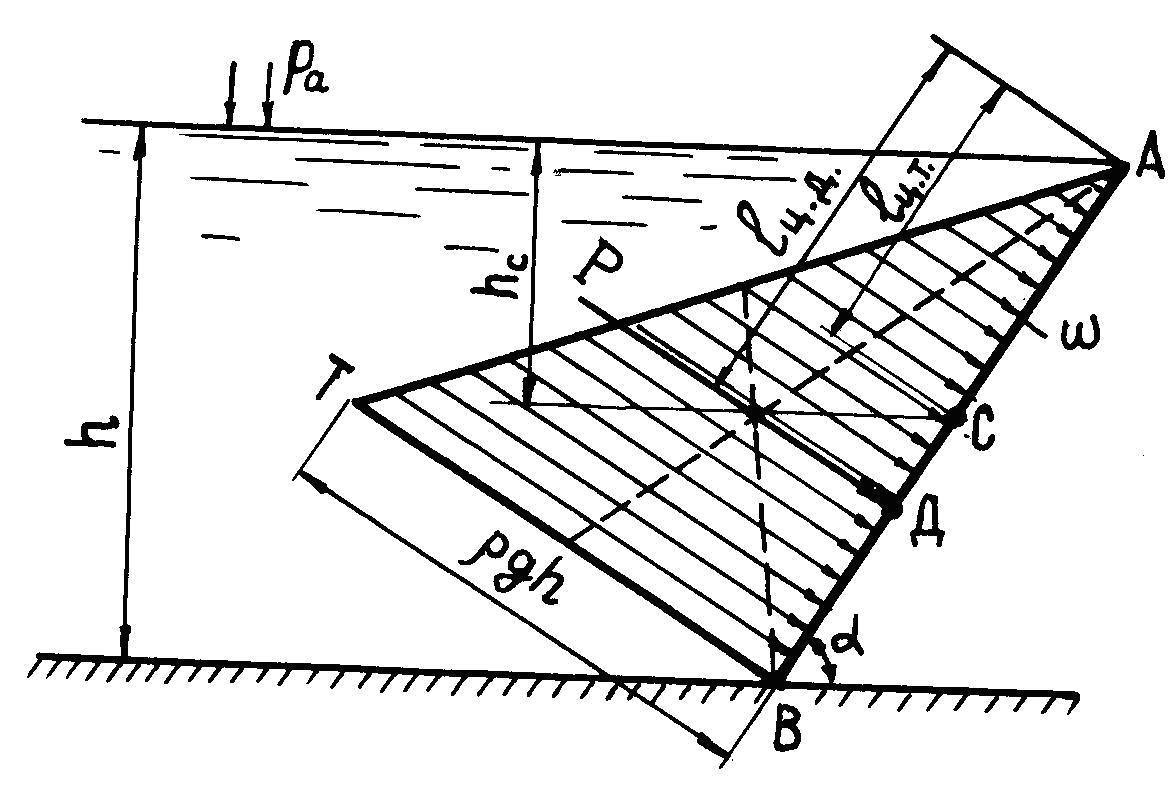
Рисунок 2.1
Закон
Паскаля: «Внешнее давление
![]() ,
приложенное к свободной поверхности
жидкости, передается всем точкам этой
жидкости и по всем направлениям
одинаково.»
,
приложенное к свободной поверхности
жидкости, передается всем точкам этой
жидкости и по всем направлениям
одинаково.»
Как видно из (2.6), сила избыточного гидростатического давления на плоскую поверхность равна произведению площади смоченной поверхности на величину избыточного гидростатического давления в ее центре тяжести.
Точка
приложения силы
![]() называется центром давления (на рисунке
2.1 - точка Д), положение которого
определяется по зависимости:
называется центром давления (на рисунке
2.1 - точка Д), положение которого
определяется по зависимости:
![]() , (2.7)
, (2.7)
где ![]() - расстояние от линии уреза жидкости до
центра давления силы
- расстояние от линии уреза жидкости до
центра давления силы![]() (для наклонных поверхностей измеряется
по наклону, для вертикальных поверхностей
- по вертикали);
(для наклонных поверхностей измеряется
по наклону, для вертикальных поверхностей
- по вертикали);
![]() - расстояние от линии уреза жидкости до
центра тяжести смоченной плоской
поверхности (то же, для наклонных
поверхностей измеряется по наклону,
для вертикальных - по вертикали);
- расстояние от линии уреза жидкости до
центра тяжести смоченной плоской
поверхности (то же, для наклонных
поверхностей измеряется по наклону,
для вертикальных - по вертикали);
![]() - момент инерции плоской поверхности
относительно горизонтальной оси,
проходящей через центр тяжести площади,
равный для прямоугольных поверхностей:
- момент инерции плоской поверхности
относительно горизонтальной оси,
проходящей через центр тяжести площади,
равный для прямоугольных поверхностей:
![]() , (2.8)
, (2.8)
где ![]() и
и![]() - ширина и длина поверхности.
- ширина и длина поверхности.
При
наличии воды с двух сторон поверхности
определяются силы ГСД, действующие
слева
![]() и справа
и справа![]() ,
а также расстояния
,
а также расстояния![]() и
и![]() ,
определяющие положение центра давления
этих сил. Так как силы
,
определяющие положение центра давления
этих сил. Так как силы![]() и
и![]() ,
согласно свойства, будут направлены
нормально к поверхности, то равнодействующая
двух параллельных и противоположно
направленных сил будет равна их разности
,
согласно свойства, будут направлены
нормально к поверхности, то равнодействующая
двух параллельных и противоположно
направленных сил будет равна их разности
![]() (2.9)
(2.9)
и направлена в сторону большей силы.
Центр давление равнодействующей силы определяется с помощью теоремы Вариньона о моменте равнодействующей: «Момент равнодействующей силы относительно некоторой оси (точки) равен сумме моментов сил ее составляющих относительно той же оси (точки)».
Сила
давления жидкости на плоскую поверхность
и положения ее центра давления могут
быть определены графоаналитическим
способом с помощью построения эпюры
[Альтшуль,с.30] избыточного гидростатического
давления, графически изображающей закон
распределения давления с изменением
глубины погружения точки в виде уравнения
прямой
![]() ,
показывающей величину и направление
давления в любой точке на поверхности
и позволяющей найти величину и точку
приложения силы давления.
,
показывающей величину и направление
давления в любой точке на поверхности
и позволяющей найти величину и точку
приложения силы давления.
При
графоаналитическом расчете в принятом
линейном масштабе вычерчивается
расчетная схема. Для построения эпюры
гидростатического давления определяется
давление воды в двух крайних точках
поверхности по зависимости
![]() ,
где
,
где![]() - глубина погружения верхней и нижней
точки.
- глубина погружения верхней и нижней
точки.
Через концы отрезков, равных по величине давления в рассматриваемых крайних точках и отложенных со стороны воды в принятом масштабе перпендикулярно к поверхности, проводится прямая линия, ограничивающая эпюру гидростатического давления. Если верхняя точка плоской поверхности находится на свободной поверхности воды, то эпюра давления будет выглядеть в виде треугольника (рисунок 2.1), если верхняя точка поверхности заглублена, то эпюра давления воды будет трапецией.
Эпюра давления штрихуется по направлению действия давления, т.е. нормально к поверхности. Каждый отрезок штриховки со стрелкой на конце в масштабе изображает величину и направление давления в данной точке на плоской поверхности.
Сила
гидростатического давления на плоскую
прямоугольную поверхность шириной
![]() равна:
равна:
![]() , (2.10)
, (2.10)
где ![]() - площадь эпюры давления.
- площадь эпюры давления.
Сила
![]() переходит через центр тяжести эпюры
давления и направлена перпендикулярно
к плоской поверхности. Положение центра
тяжести эпюры определяется графически
известными способами - если эпюра
выглядит в виде треугольника, как
показано на рисунке 2.2,а, то центр тяжести
определяется пересечением медиан, если
в виде трапеции, то можно воспользоваться
графическим построением, как показано
на рисунке 2.2,б.
переходит через центр тяжести эпюры
давления и направлена перпендикулярно
к плоской поверхности. Положение центра
тяжести эпюры определяется графически
известными способами - если эпюра
выглядит в виде треугольника, как
показано на рисунке 2.2,а, то центр тяжести
определяется пересечением медиан, если
в виде трапеции, то можно воспользоваться
графическим построением, как показано
на рисунке 2.2,б.
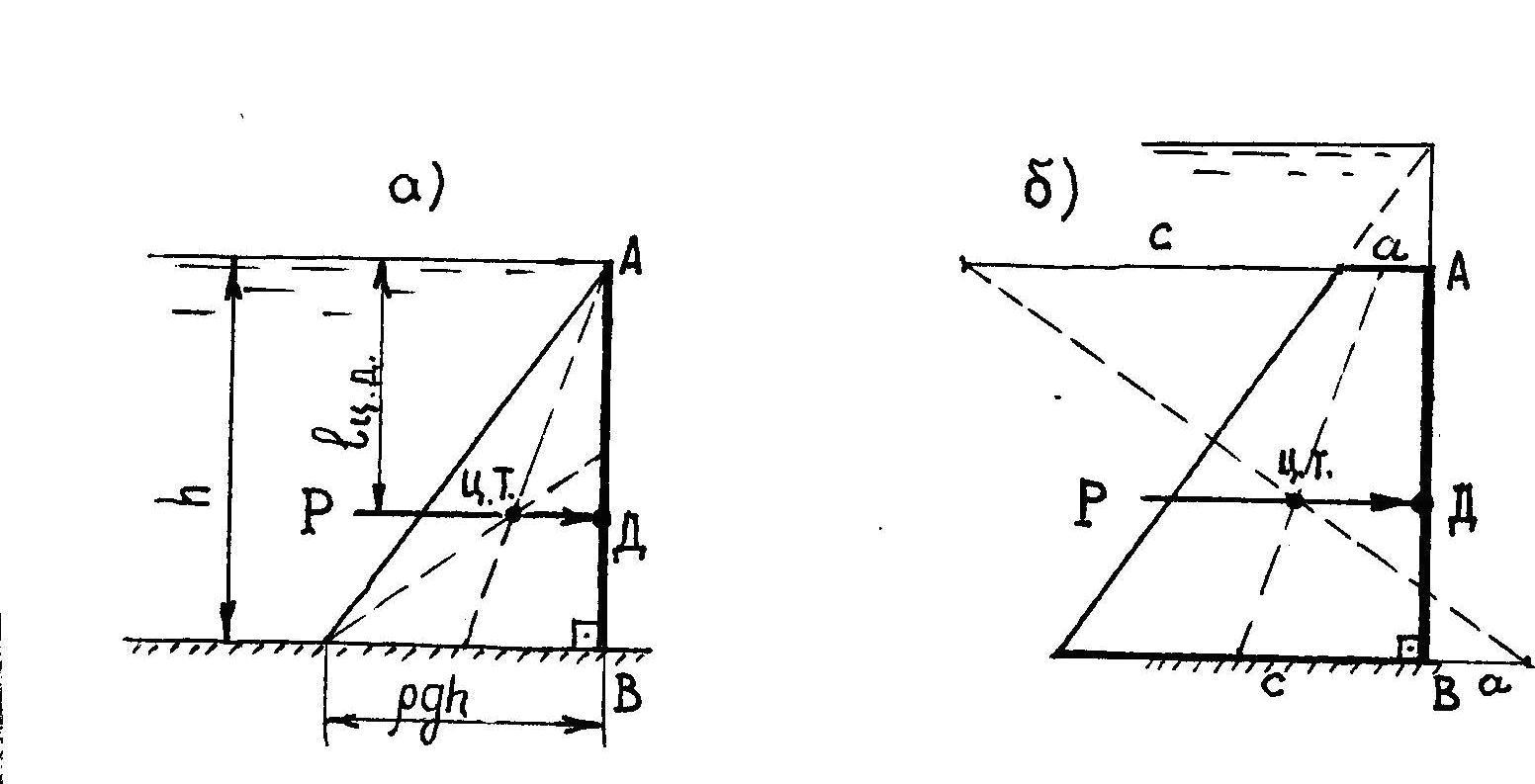
Рисунок 2.2
При
наличии воды с двух сторон, как показано
на рисунке 2.3, строятся две эпюры ГСД от
действия воды слева и справа. Так как
эпюры имеют противоположное направление
действия давления, то строится суммарная
эпюра давления (ABKL), которая будет равна
разности этих эпюр. Равнодействующая
сила гидростатического давления на
плоскую поверхность определяется по
суммарной эпюре давления, используя
зависимость (2.10). Сила
![]() проходит через центр тяжести эпюры
давления перпендикулярно к плоской
поверхности (затвора, стенки).
проходит через центр тяжести эпюры
давления перпендикулярно к плоской
поверхности (затвора, стенки).
Суммарная эпюра давления может быть в виде прямоугольника, трапеции или пятиугольника. Центр тяжести прямоугольника лежит на пересечении диагоналей, трапеции - определяется известным графическим построением. Центр тяжести для суммарной эпюры в виде пятиугольника можно найти также графическим построением, изложенным ниже.
Центр
давления, т.е. точка
![]() приложения силы ГСД, лежит на самой
поверхности (затвора, стенки) и определяется
пересечением линии действия силы с
поверхностью.
приложения силы ГСД, лежит на самой
поверхности (затвора, стенки) и определяется
пересечением линии действия силы с
поверхностью.
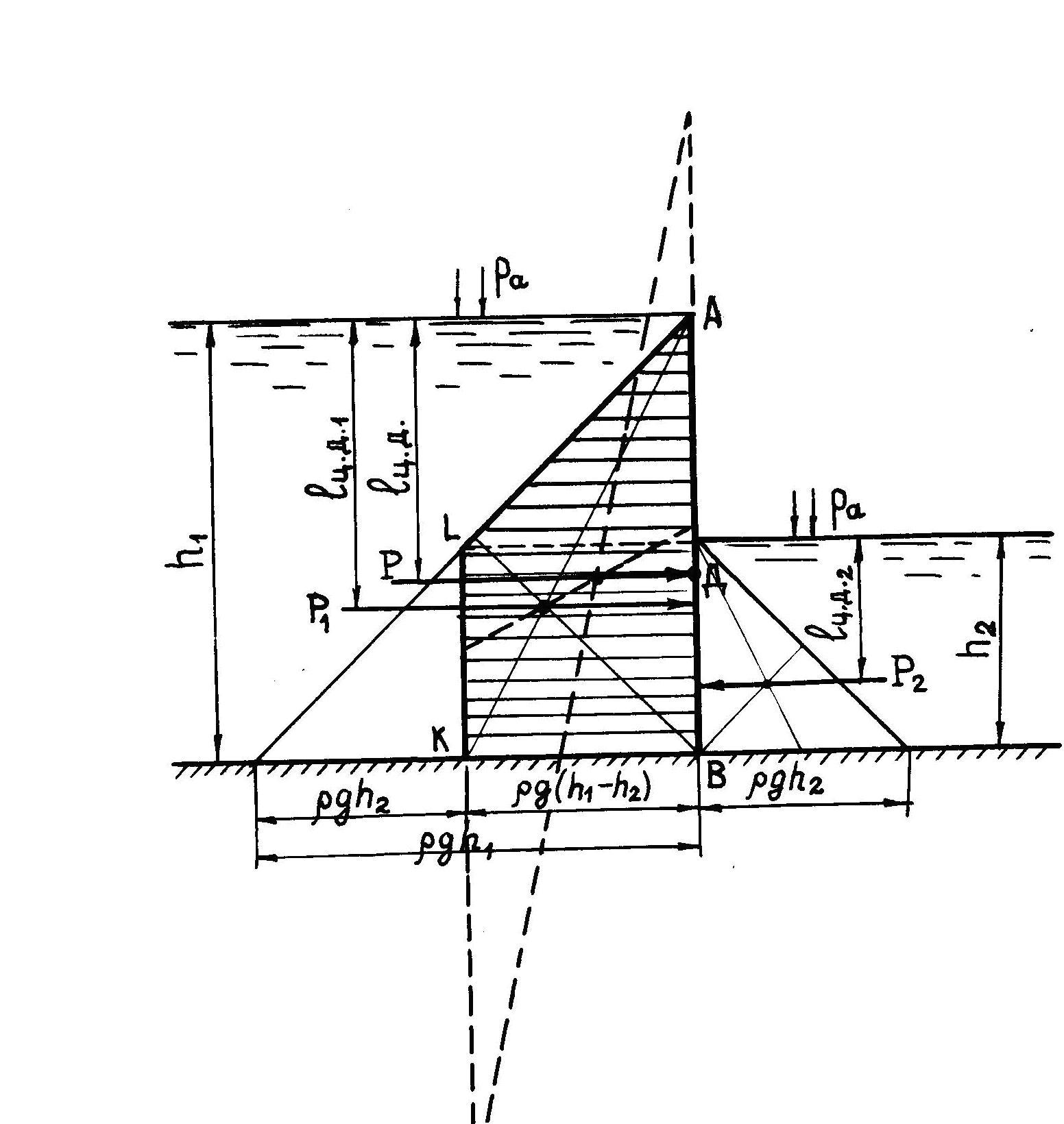
Рисунок 2.3
Пример расчета.
Задача.
Определить:
аналитическим и графоаналитическим
способами величину силы ГСД и точку ее
приложения, т.е.
![]() и
и![]() (рис.
2.4), если дано:
(рис.
2.4), если дано:
![]() - ширина затвора;
- ширина затвора;
![]() - угол наклона затвора
- угол наклона затвора![]() к горизонту;
к горизонту;
![]() - высота отверстия, перекрываемого
затвором.
- высота отверстия, перекрываемого
затвором.
Решение.
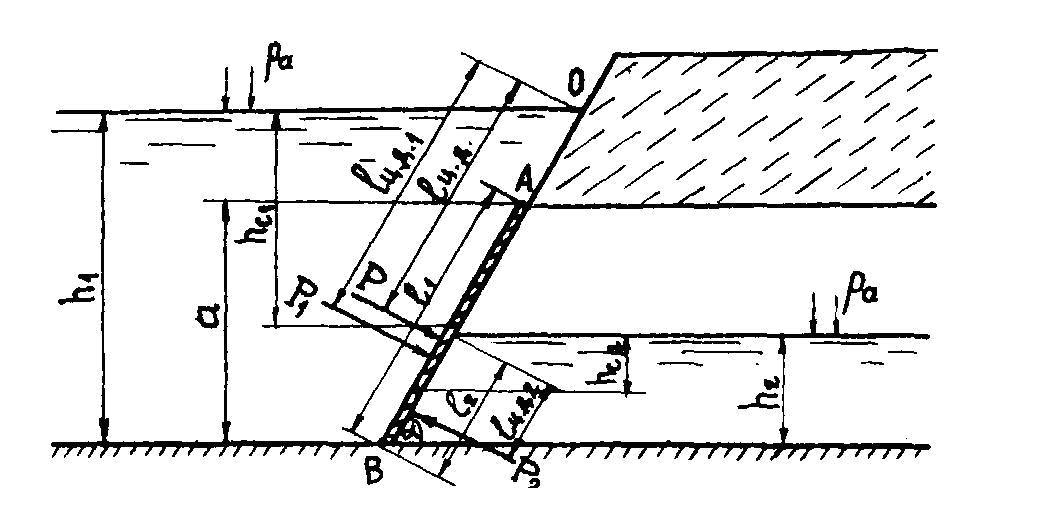
Рисунок 2.4 – Расчетная схема гидротехнического сооружения с плоским затвором АВ
Аналитическое решение
Сила
ГСД на затвор
![]() от действия воды слева определяется по
формуле (2.6):
от действия воды слева определяется по
формуле (2.6):
![]() ,
кН,
,
кН,
где
![]() ;
;
![]()
![]() - длина смоченной поверхности затвора
водой, расположенной слева.
- длина смоченной поверхности затвора
водой, расположенной слева.
По аналогии определяется сила ГСД на затвор от действия воды справа:
![]() ,
кН,
,
кН,
где
![]() ;
;
![]()
![]() - длина смоченной поверхности затвора
водой, расположенной справа.
- длина смоченной поверхности затвора
водой, расположенной справа.
Равнодействующая сила ГСД двух параллельных и противоположно направленных сил будет равна:
![]() ,
кН
,
кН
и
направлена в сторону большей силы
![]() .
.
Положение
центра давления для силы
![]() определяется по формуле (2.7):
определяется по формуле (2.7):
![]() ,
,
где
![]() ,
,
![]() ,
м4.
,
м4.
По
аналогии определяется положение центра
давления для силы
![]() .
.
Сила
![]() от действия воды справа будет приложена
к затвору на расстоянии 2/3 его длины,
считая от линии уреза воды, или на глубине
2/3 от уровня воды.
от действия воды справа будет приложена
к затвору на расстоянии 2/3 его длины,
считая от линии уреза воды, или на глубине
2/3 от уровня воды.
Для
определения положения центра давления
равнодействующей силы
![]() используем теорему Вариньона. Составим
уравнение моментов относительно точки
О.
используем теорему Вариньона. Составим
уравнение моментов относительно точки
О.
![]() ,
,
где
![]() .
.
Откуда
определяем
![]() .
.
Графоаналитическое решение
В
линейном масштабе 1:50 или 1:100 вычерчивается
на миллиметровке расчетная схема
сооружения. Далее, в принятом соответственно
масштабе давления в 1 см - 5 кН/м2
или в 1 см - 10 кН/м2,
используя зависимость
![]() ,
строятся эпюры избыточного гидростатического
давления на затвор слева (трапеция ABNM)
и справа (треугольник СВЕ), как показано
на рисунке 2.5.
,
строятся эпюры избыточного гидростатического
давления на затвор слева (трапеция ABNM)
и справа (треугольник СВЕ), как показано
на рисунке 2.5.
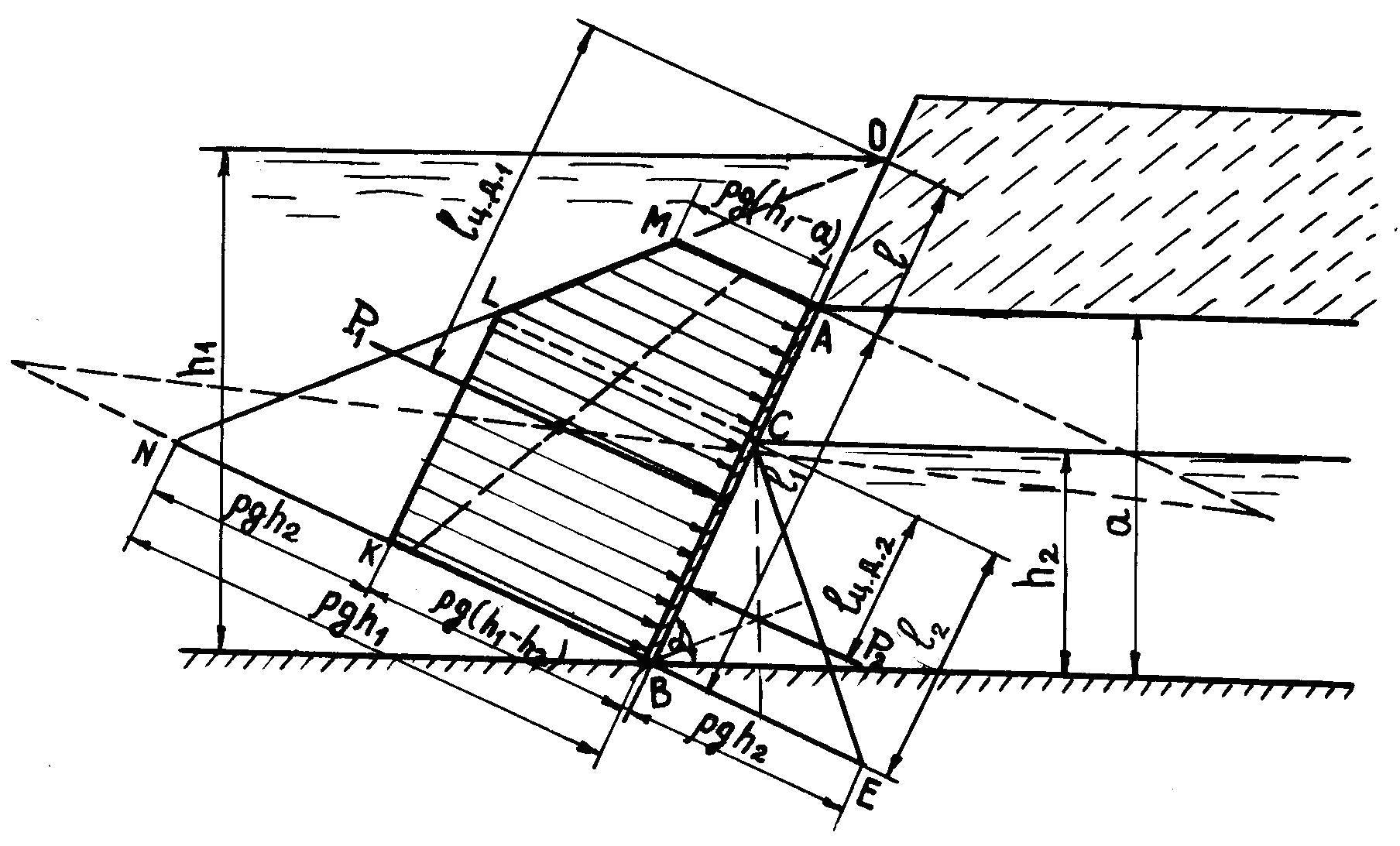
Рисунок 2.5
Равнодействующая эпюра давления, представляющая разность эпюр слева и справа, изобразится для рассматриваемой схемы в виде пятиугольника ABKLM.
С помощью эпюр по зависимости (1.10) определяются силы:
![]() ,
,
![]() ,
,
![]() .
.
Сила
![]() проходит через центр тяжести эпюры в
виде трапеции ABNM, сила
проходит через центр тяжести эпюры в
виде трапеции ABNM, сила![]() - через центр тяжести треугольника СВЕ
нормально к поверхности затвора.
- через центр тяжести треугольника СВЕ
нормально к поверхности затвора.
Центры тяжести трапеции и треугольника находятся графическими приемами, рассмотренными выше, как показано на рисунке 2.2.
Для
определения центра тяжести суммарной
эпюры давления в виде пятиугольника
ABKLM, через которой должна пройти
равнодействующая сила
![]() ,
необходимо выполнить графическое
построение, как показано на рисунке
2.6.
,
необходимо выполнить графическое
построение, как показано на рисунке
2.6.

Рисунок 2.6
Эпюра
ABKLM разбивается в двух перпендикулярных
направлениях линиями LC и MR на простые
геометрические фигуры – соответственно
трапецию ACLM и прямоугольник CBKL, трапецию
MRKL и прямоугольник ABRM. Известными
графическими приемами определяются
центры тяжести простых фигур. Полученные
центры тяжести каждых двух соответствующих
фигур соединяются линиями. Пересечение
линий, соединяющих центры тяжести
простых фигур, определит положение
центра тяжести суммарной эпюры в точке
Ц. Через центр тяжести проходит
равнодействующая сила
![]() нормально к поверхности затвора.
нормально к поверхности затвора.
Точка
пересечения линии действия силы
![]() и поверхности затвора есть центр
давления, положение которого определяется
расстоянием
и поверхности затвора есть центр
давления, положение которого определяется
расстоянием![]() ,
измеренным с учетом линейного масштаба
по наклону от линии уреза воды в точке
,
измеренным с учетом линейного масштаба
по наклону от линии уреза воды в точке![]() до центра давления в точке
до центра давления в точке![]() ,
как показано на рисунке 2.6.
,
как показано на рисунке 2.6.
Значения
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
полученные графоаналитическим способом,
сравниваются для проверки с вычисленными
аналитически.
,
полученные графоаналитическим способом,
сравниваются для проверки с вычисленными
аналитически.
