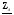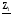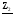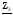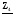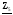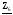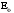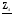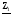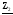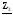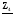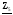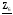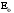трехфазные цепи
.docx5.0. Задача №5. Расчёт трёхфазной электрической цепи синусоидального тока
Задание задачи рассчитано на освоение студентами метода расчёта простой трёхфазной электрической цепи синусоидального тока при неравномерной нагрузке фаз [1-6].
5.1. Постановка задачи
На рис.5 представлены варианты электрических схем трёхфазной электрической цепи при симметричной трёхфазной системе ЭДС и неравномерной нагрузки фаз. Для схем в таблице 5 приведены числовые значения параметров и фазных ЭДС для каждого варианта задания.
Требуется:
-
Определить линейные и фазные токи, падения напряжения на всех элементах схемы.
-
Для исходной схемы проверить правильность нахождения всех токов по балансу мощностей.
-
Построить топографическую диаграмму, совмещённую с векторной диаграммой токов.
-
Разложить трёхфазные системы линейных токов и фазных напряжений нагрузки на симметричные составляющие. Правильность разложения на симметричные составляющие проверить геометрически.
5.2. Порядок расчёта [6]
1. Исходную схему преобразовать к схеме «Y-Y» без нейтрального провода. Полученную эквивалентную схему рассчитать с помощью метода двух узлов:
-
найти напряжение между двумя нейтральными точками нагрузки и генератора;
-
используя обобщённый закон Ома определить линейные токи;
-
найти фазные и линейные падения напряжения на эквивалентной нагрузке и в линейных проводах;
-
определить оставшиеся токи в исходной схеме.
2. Составить баланс полных комплексных мощностей, проверить его соблюдение по относительным ошибкам.
3. В исходной схеме заземлить нейтральную точку генератора и определить потенциалы остальных точек относительно заземлённой. Построить топографическую диаграмму, совмещённую с векторной диаграммой токов.
4. Вычислить симметричные составляющие прямой, обратной и нулевой последовательностей фаз для линейных токов и фазных напряжений. Проверить на комплексной плоскости для тока и напряжения фазы «А» правильность найденных разложений путём сложения векторов, например, для тока должно выполняться равенство:
IA = IA1 + IA2 + IA0 ,
где векторы IA1, IA2 и IA0 – токи прямой, обратной и нулевой последовательностей фаз соответственно. Замечание, для исходных схем ток нулевой последовательности фаз должен быть равен нулю, т.к. нет нейтрального провода.
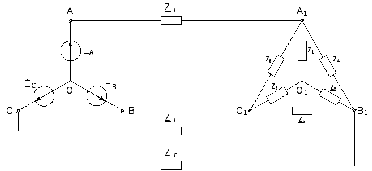
1)
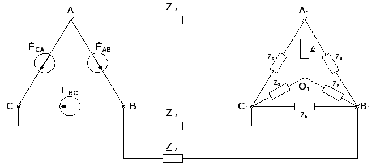
2)
Рис.5. Два варианта схемы представленных в таблице 5.
Таблица 5
|
№ вари-анта |
№ варианта схемы на рис. 5 |
|
|
|
|
|
|
|
|
|
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
В |
||
|
1 |
1 |
2+j2 |
10+j10 |
15-j10 |
10+j14 |
13+j10 |
0+j20 |
20+j0 |
110 |
|
2 |
2 |
2+j3 |
15- j10 |
10+ j12 |
10+ j0 |
10+ j5 |
0 –j15 |
15 –j8 |
115 |
|
3 |
1 |
2 +j4 |
12+ j14 |
16 +j20 |
13+j10 |
16 +j20 |
13+ j14 |
15- j10 |
120 |
|
4 |
2 |
2 +j5 |
19+j14 |
10+ j16 |
15- j15 |
16 +j20 |
13+ j14 |
15- j10 |
127 |
|
5 |
1 |
3 + j2 |
15+ j20 |
12+ j15 |
15+j20 |
13- j13 |
10- j10 |
20+j0 |
200 |
|
6 |
2 |
3 + j4 |
15- j8 |
15+ j8 |
10+ j12 |
14+j6 |
10+j14 |
0+j14 |
205 |
|
7 |
1 |
4 + j4 |
10+ j12 |
10- j18 |
12+j14 |
14- j14 |
12+ j14 |
12+j0 |
215 |
|
8 |
2 |
3 + j3 |
10- j18 |
10+ j10 |
10- j18 |
13+ j18 |
18+j0 |
0- j18 |
220 |
|
9 |
1 |
4 +j5 |
16+ j20 |
15+ j18 |
15- j15 |
13+ j19 |
12+ j18 |
20+ j0 |
110 |
|
10 |
2 |
3 + j5 |
10+ j15 |
20+ j14 |
12+j15 |
0- j20 |
20+j15 |
16+ j19 |
115 |
|
11 |
1 |
3 + j2 |
10- j10 |
15- j0 |
18+j10 |
13+j10 |
10+j20 |
20+j0 |
120 |
|
12 |
2 |
3 + j4 |
0- j10 |
10+ j12 |
10+ j15 |
10+ j5 |
15 –j15 |
0 –j8 |
127 |
|
13 |
1 |
4 + j4 |
12+ j0 |
16 +j20 |
13- j10 |
0 +j20 |
13+ j14 |
15+ j10 |
200 |
Продолжение таблицы 5
|
№ вари-анта |
№ варианта схемы на рис. 5 |
|
|
|
|
|
|
|
|
|
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
В |
||
|
14 |
2 |
3 + j3 |
19- j14 |
10+ j10 |
15- j15 |
20- j15 |
12- j16 |
16+ j0 |
205 |
|
15 |
1 |
4 +j5 |
15+ j20 |
12- j15 |
15+j15 |
0- j13 |
10+ j10 |
20+j0 |
215 |
|
16 |
2 |
3 + j5 |
0- j18 |
15+ j18 |
10+ j0 |
14-j16 |
10+j14 |
10+j14 |
220 |
|
17 |
1 |
2+j2 |
10+ j12 |
10+ j18 |
12+j0 |
0- j14 |
12+ j14 |
12+j10 |
110 |
|
18 |
2 |
2+j3 |
10+ j18 |
10+ j10 |
0- j18 |
13- j18 |
18+j0 |
10- j18 |
115 |
|
19 |
1 |
2 +j4 |
16+ j20 |
15- j18 |
0- j15 |
13+ j0 |
12+ j18 |
20+ j0 |
120 |
|
20 |
2 |
2 +j5 |
0+ j15 |
20+ j0 |
12- j15 |
10- j20 |
20+j15 |
16+ j19 |
127 |
|
21 |
1 |
3 + j2 |
10+j10 |
15-j10 |
10+j14 |
10+ j5 |
0 –j15 |
15 –j8 |
200 |
|
22 |
2 |
4 +j5 |
15- j10 |
10+ j12 |
10+ j0 |
16 +j20 |
13+ j14 |
15- j10 |
205 |
|
23 |
1 |
3 + j5 |
16 +j20 |
13+ j14 |
15- j10 |
15- j10 |
10+ j12 |
10+ j0 |
215 |
|
24 |
2 |
3 + j2 |
12+ j14 |
16 +j20 |
13+j10 |
12+ j14 |
16 +j20 |
13+j10 |
220 |
|
25 |
1 |
2+j2 |
15- j10 |
10+ j12 |
10+ j0 |
16 +j20 |
13+ j14 |
15- j10 |
110 |
|
26 |
2 |
2+j3 |
13+ j18 |
18+j0 |
0- j18 |
12+ j14 |
16 +j20 |
13+j10 |
115 |
|
27 |
1 |
2 +j4 |
12+ j14 |
16 +j20 |
13+j10 |
13+ j19 |
12+ j18 |
20+ j0 |
120 |
|
28 |
2 |
2 +j5 |
13- j13 |
10- j10 |
20+j0 |
15- j10 |
10+ j12 |
10+ j0 |
127 |
|
29 |
1 |
4 +j5 |
0- j20 |
20+j15 |
16+ j19 |
12+ j14 |
16 +j20 |
13+j10 |
200 |
|
30 |
2 |
3 + j5 |
13+j10 |
10+j20 |
20+j0 |
19+j14 |
10+ j16 |
15- j15 |
205 |
|
31 |
1 |
2+j2 |
14+j6 |
10+j14 |
0+j14 |
15- j10 |
10+ j12 |
10+ j0 |
360 |
|
32 |
2 |
2+j3 |
13+j10 |
0+j20 |
20+j0 |
15- j8 |
15+ j8 |
10+ j12 |
365 |
|
33 |
1 |
2 +j4 |
19+j14 |
10+ j16 |
15- j15 |
10+ j5 |
15 –j15 |
0 –j8 |
370 |
|
34 |
2 |
2 +j5 |
15- j10 |
10+ j12 |
10+ j0 |
14- j14 |
12+ j14 |
12+j0 |
375 |
|
35 |
1 |
3 + j2 |
15- j8 |
15+ j8 |
10+ j12 |
16 +j20 |
13+ j14 |
15- j10 |
380 |