ТАУ лаба 1 вариант 9

Лабораторная работа №1

Моделирование звеньев автоматических систем

Вариант 9

Выполнил:

П.Н. Чехин, студент группы МР-10-1

Принял:

Н.Н. Куцый

Цель работы

Ознакомление с методами моделирования автоматических систем; непосредственное моделирование типовых звеньев; расчет временных характеристик звеньев.

Задана передаточная функция колебательного звена:

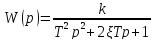
Значения параметров звена:

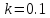
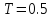
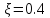
Представим уравнения моделирования на основе способа комбинирования производных:

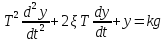
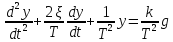
Здесь имеем:

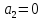
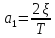
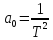
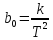
Введем новую переменную

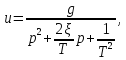
где 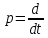- оператор дифференцирования.

В результате получаем

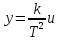
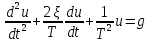
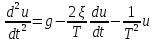
Сделаем ввод новых переменных

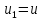
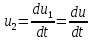
Тогда получаем

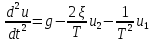
Применим метод Рунге-Кутты

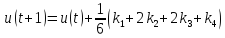
Выбор шага интегрирования при численном интегрировании дифференциальных уравнений автоматических систем можно провести по следующей приближенной методике:

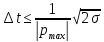
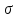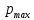Относительную допустимую методическую погрешность , задаваемую из практических соображений, примем равной 0.001. Величина – наибольший по модулю корень характеристического уравнения.

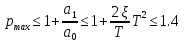
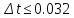
Интервал интегрирования L в звеньях второго порядка оценивается как

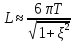
В данном случае выбираем .

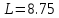Листинг фрагмента программы, относящегося к моделированию заданного звена:

const

Lin = 8.75; //интервал моделирования

dt = 0.032; //шаг интегрирования

ksi=0.4;

k=0.1;

T=0.5;

g=1.0;

var

sumdt, //текущее время моделирования

y,y1,y2,ypr, //переходная функция

u,u1,u2,

k11,k12,k21,k22,k31,k32,k41,k42,

w //весовая функция

: Real;

begin

////////////////////////////////////////////

//НАЧАЛЬНЫЕ УСЛОВИЯ

sumdt:=0;

y:=0; ypr:=0; y1:=0; y2:=0;

////////////////////////////////////////////

//НАЧАЛО МОДЕЛИРОВАНИЯ

REPEAT

////////////////////////////////////////////

//УРАВНЕНИЯ ПЕРЕХОДНОГО ПРОЦЕССА

k11:=u2*dt;

k12:=(g-2*ksi/T*u2-1/sqr(T)*u1)*dt;

k21:=(u2+(k12/2))*dt;

k22:=(g-(2*ksi/T)*(u2+k12/2)-(1/(T*T))*(u1+k11/2))*dt;

k31:=(u2+(k22/2))*dt;

k32:=(g-(2*ksi/T)*(u2+k22/2)-(1/(T*T))*(u1+k21/2))*dt;

k41:=(u2+k32)*dt;

k42:=(g-(2*ksi/T)*(u2+k32)-(1/(T*T))*(u1+k31))*dt;

u1:=u1+(k11+2*k21+2*k31+k41)/6;

u2:=u2+(k12+2*k22+2*k32+k42)/6;

y:=k/sqr(T)*u1;

w:=(y-ypr)/dt;

ypr:=y;

//ВЫВОД ГРАФИКОВ

Graphic1.AddXY(sumdt,Y); //первый график

Graphic2.AddXY(sumdt,w); //второй график

Graphic3.AddXY(sumdt,g); //третий график

sumdt:=sumdt+dt; //увеличение текущего времени на dt

UNTIL sumdt>=Lin;

//КОНЕЦ МОДЕЛИРОВАНИЯ

////////////////////////////////////////////

end;

end.

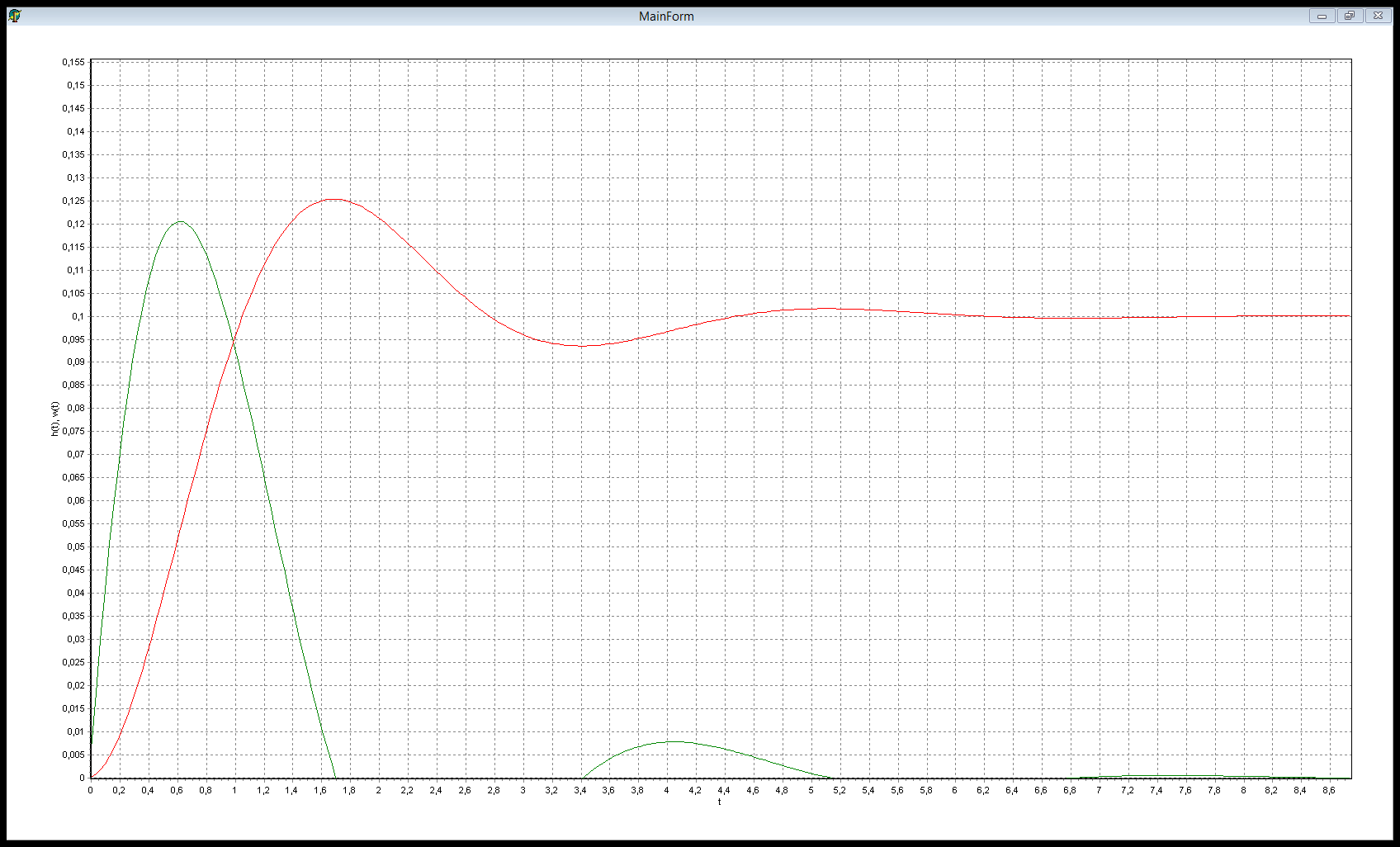
Полученные графики переходной и весовой функций

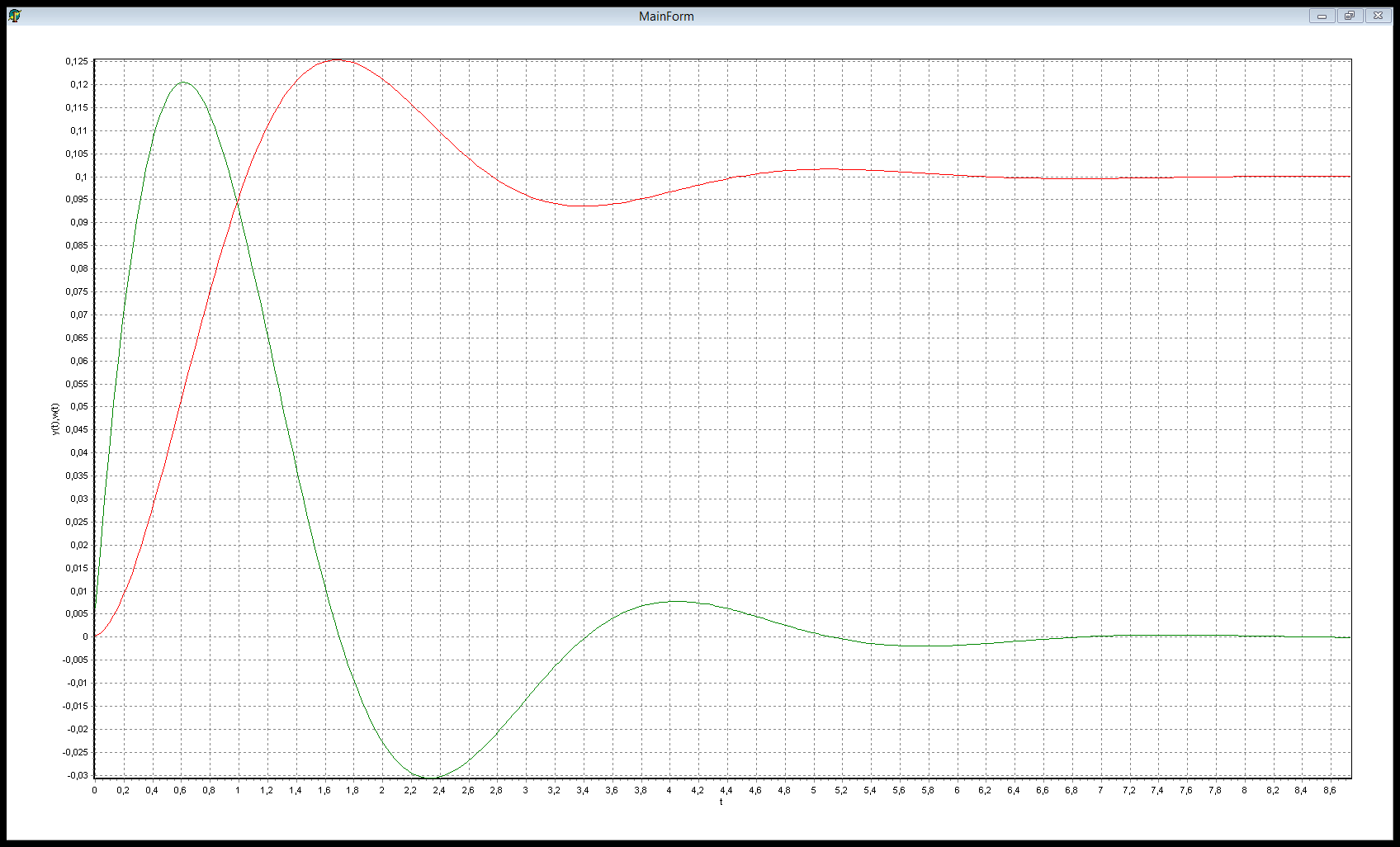
Из графика переходной функции определяем следующие временные характеристики:

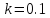
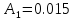
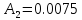
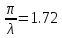
Отсюда, находим:

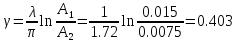
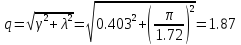
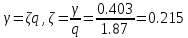
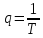
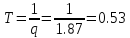
Полученные параметры практически совпали с заданными значениями.

k

Получение аналитических выражений переходной и весовой функций классическим методом

Дифференциальное уравнение передаточной функции звена задано в виде

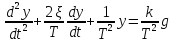
Запишем характеристическое уравнение:

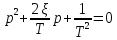
Корни характеристического уравнения

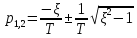
Введем обозначение

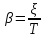
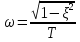
Тогда

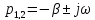
Общее решение однородного дифференциального уравнения

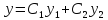
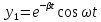
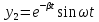
Запишем систему уравнений

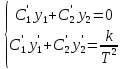
Производные записываются в виде

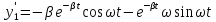
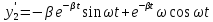
Отсюда имеем:

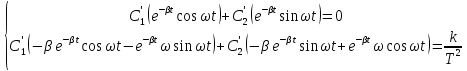
Выразим из первого уравнения

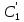
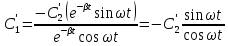
Подставим во второе уравнение:

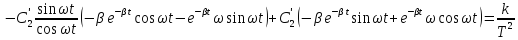
Выполним некоторые преобразования

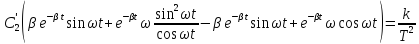
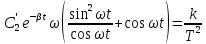
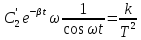
Отсюда

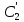
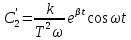
Проинтегрируем полученное выражение и найдем

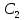
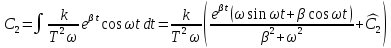
Из первого уравнения имеем

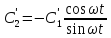
Подставим во второе уравнение и выразим

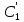
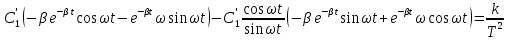
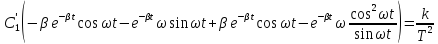
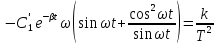
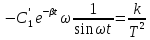
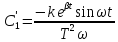
Проинтегрируем полученное выражение и найдем

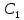
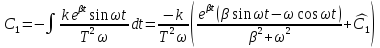
Имеем

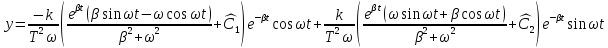
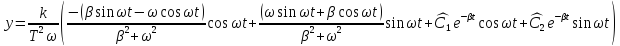
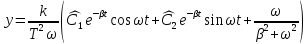
Определим постоянные, исходя из начальных условий

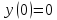
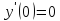
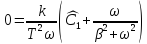
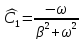
Производная y’

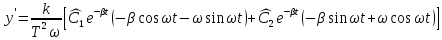
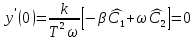
Отсюда

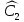
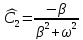
Возвращаемся к выражению для y

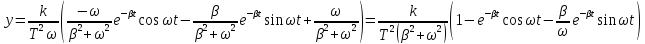
Рассмотрим отдельно

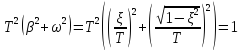
Тогда окончательно, переходная функция

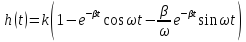
Весовая функция

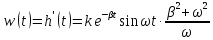
Выполним построение графиков полученных функций: