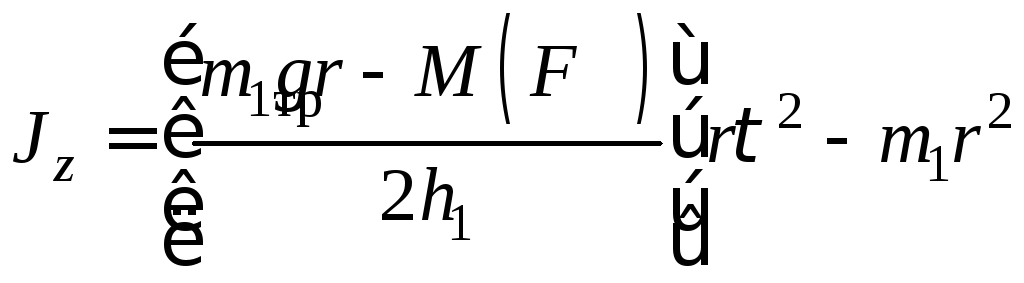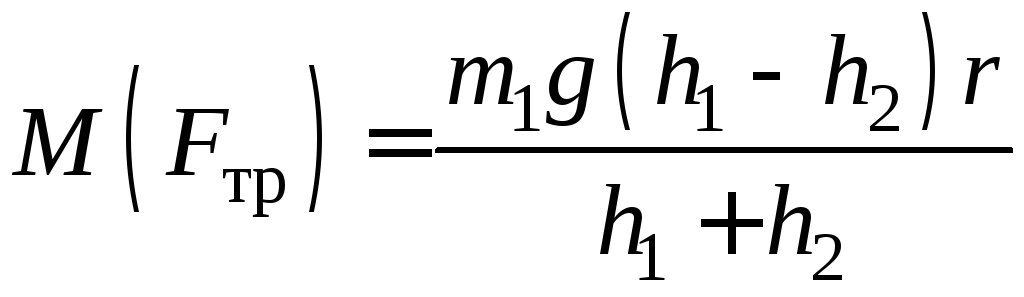Лабораторная работа № 127
Изучение динамики вращательного движения маховика
Цель работы – экспериментальное определение момента инерции маховика.
1. Теоретические основы работы
Аналогом второго закона Ньютона, справедливого для описания поступательного движения тела массой m
|
|
(1) |
во вращательном движении, является основное уравнение динамики вращательного движения
|
|
(2) |
где
![]() и
и![]() соответственно момент инерции и угловое
ускорение твердого тела относительно
неподвижной оси вращенияz,
соответственно момент инерции и угловое
ускорение твердого тела относительно
неподвижной оси вращенияz,
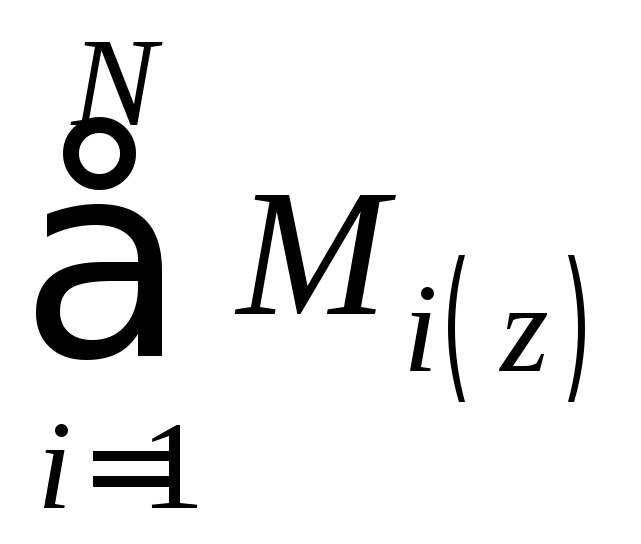 – алгебраическая сумма моментов сил
относительно осиz.
– алгебраическая сумма моментов сил
относительно осиz.
Сравнительный анализ уравнений (1) и (2) показывает, что роль массы в поступательном движении играет момент инерции тела во вращательном движении. А поскольку масса является мерой инертности тела в поступательном движении, то момент инерции является также мерой инертности тела во вращательном движении. В этом заключается физический смысл момента инерции.
Относительно неподвижной оси z момент инерции твердого тела определяется по формуле
|
|
(3) |
где r является кратчайшим расстоянием от элемента тела массой dm до оси z.
Из формулы (3) следует, что момент инерции зависит от массы тела и от ее распределения относительно оси вращения. Чем больше масса тела и чем дальше она находится от оси вращения, тем больше момент инерции твердого тела и наоборот.
Рассмотрим маховик (рис.1), состоящий из диска, шкива и вала. Предположим, что они обладают общей массой М. Диск и шкив насажены на общий вал, закрепленный в подшипниках. Маховик может вращаться относительно оси z, совпадающей с осью вала (на рис.1 ось z перпендикулярна плоскости чертежа и направлена «от нас»).

Рис.1 Схема системы маховик-груз (вал на схеме не показан)
Вращение маховика осуществляется под действием груза массой m1, укрепленного на нити, намотанной на шкив, и описывается относительно неподвижной оси z уравнением
|
|
(4) |
где
![]() момент инерции маховика,
момент инерции маховика,![]() –его угловое
ускорение,
–его угловое
ускорение,
 –
сумма моментов сил, действующих на
маховик.
–
сумма моментов сил, действующих на
маховик. включает момент силы натяжения нитиМ(Т2)
и момент силы трения
М(Fтр)
в подшипниках вала. Моменты сил N
и Мg
относительно оси z
равны нулю. Таким образом
включает момент силы натяжения нитиМ(Т2)
и момент силы трения
М(Fтр)
в подшипниках вала. Моменты сил N
и Мg
относительно оси z
равны нулю. Таким образом
|
|
(5) |
Поступательное движение груза массой m1 описывается вторым законом Ньютона
|
|
(6) |
где а является ускорением центра масс груза, Т1 – силой натяжения нити, приложенной к грузу. В проекции на ось у уравнение (6) принимает вид
|
|
(7) |
Так как предполагается, что нить нерастяжима и невесома, то ускорение всех точек нити и груза одинаковы, причем в отсутствии проскальзывания нити линейное (тангенциальное) ускорение обода диска равно ускорению груза. Силы натяжения нити Т1 и Т2 равны между собой (Т1 = Т2 = Т) по третьему закону Ньютона.
Предположим, нить полностью намотана на шкив и груз находится в крайнем верхнем положении. При отпускании маховика нить под действием груза массой m1 , будет разматываться. Груз в процессе движения всей системы опустится в крайнее нижние положение, пройдя путь h1. Тогда с учетом, что
|
|
(8) |
где – время движения груза, а
|
|
(9) |
имеем
|
|
(10) |
Из уравнения (5) находим
|
|
(11) |
Силу натяжения Т выражаем из уравнения (7), а угловое ускорение – из (10). Затем полученные формулы для Т и подставляем в (11). В итоге получаем
|
|
(12) |
Для расчета
![]() нужно знать все величины, входящие в
формулу (12). Они определяются
экспериментально:
нужно знать все величины, входящие в
формулу (12). Они определяются
экспериментально:![]() – с помощью штангенциркуля,
– с помощью штангенциркуля,![]() – с помощью линейки,
– с помощью
секундомера. Масса груза m1
изначально задана. Момент силы трения
– с помощью линейки,
– с помощью
секундомера. Масса груза m1
изначально задана. Момент силы трения
![]() определяется опытным путем. Для этого
груз еще раз поднимают на первоначальную
высоту
определяется опытным путем. Для этого
груз еще раз поднимают на первоначальную
высоту![]() (одновременно наматывая нить на шкив
маховика), а затем предоставляют его
самому себе. Груз сначала опускается
наh1
до нижней
точки – нулевого отсчета высоты (нить
при этом сматывается со шкива), а затем
(когда нить начинает наматываться на
шкив) поднимается на меньшую высоту
(одновременно наматывая нить на шкив
маховика), а затем предоставляют его
самому себе. Груз сначала опускается
наh1
до нижней
точки – нулевого отсчета высоты (нить
при этом сматывается со шкива), а затем
(когда нить начинает наматываться на
шкив) поднимается на меньшую высоту
![]() .
Спуск и подъем груза происходят в течение
некоторого времени2
. Причиной подъема груза на меньшую
высоту является наличие силы трения в
подшипниках вала. Потеря механической
энергии системы
.
Спуск и подъем груза происходят в течение
некоторого времени2
. Причиной подъема груза на меньшую
высоту является наличие силы трения в
подшипниках вала. Потеря механической
энергии системы
![]() определяется работой силы трения
определяется работой силы трения![]()
|
|
(13) |
Так как начальная
и конечная кинетические энергии
![]() и
и![]() равны нулю, то изменение механической
энергии системы равно изменению только
потенциальной энергии груза
равны нулю, то изменение механической
энергии системы равно изменению только
потенциальной энергии груза
|
|
(14) |
Работа силы трения
выражается через момент силы трения
![]() и угловое перемещение маховика
:
и угловое перемещение маховика
:
|
|
(15) |
Приравнивая правые части уравнений (14) и (15), имеем
![]()
или
|
|
(16) |
Угловое перемещение маховика равно отношению длины дуги, которую опишут за время поворота 2 точки обода шкива, к его радиусу:
|
|
(17) |
Подставляя в уравнение (16), имеем
|
|
(18) |
Полученное
выражение подставляем для
![]() в уравнение (12), получаем формулу для
определения экспериментального значения
момента инерции маховика
в уравнение (12), получаем формулу для
определения экспериментального значения
момента инерции маховика
|
|
(19) |
Экспериментально определенное значение Jzэ можно сравнить с теоретическим значением того же момента инерции Jzт для рис. 2, рассчитанного по формуле
![]() .
.
Так как материал, из которого изготовлен шкив, обладает гораздо меньшей плотностью, чем плотность стальных диска и вала, то моментом инерции шкива Jz шкива можно пренебречь.
Поэтому
![]() ,
,
где
![]()
 –момент инерции
тонкого диска,
–момент инерции
тонкого диска,![]() –
момент инерции кольца (здесьМ1
и М2
являются соответственно массами тонкого
диска и кольца, R1
– внешний радиус тонкого диска и
одновременно внутренний радиус кольца,
R2
– внешний радиус кольца).
–
момент инерции кольца (здесьМ1
и М2
являются соответственно массами тонкого
диска и кольца, R1
– внешний радиус тонкого диска и
одновременно внутренний радиус кольца,
R2
– внешний радиус кольца).
Окончательно
|
|
(20) |
Данные установки представлены в разделе 2.