6.0. Задача №6. Расчёт переходного процесса в линейной электрической цепи постоянного тока
Задание задачи рассчитано на освоение студентами основных методов расчёта переходных процессов в линейных электрических цепях [1-6].
6.1. Постановка задачи
На рисунке 6 представлены десять вариантов схем линейных электрических цепей постоянного тока, в которых происходит замыкание или размыкание ключа (коммутация). Числовые данные для схем приведены в таблице 6. Необходимо определить переходные токи или переходное падение напряжения на ёмкости в зависимости от варианта, см. последний столбец таблицы 6 следующими методами:
Классический метод расчёта.
Операторный метод расчёта.
Построить график переходного процесса.
Моделирование.
6.2. Порядок расчёта [6]
Классический метод расчёта:
для после коммутационной схемы составить систему уравнений для мгновенных значений токов и напряжений;
найти принуждённое значение тока или падения напряжения;
по методу входного сопротивления составить характеристическое уравнение и найти его корни;
по виду корней характеристического уравнения определить вид свободной составляющей тока или падения напряжения;
записать общее решение в виде суммы принуждённой и свободной составляющих тока или падения напряжения;
определить постоянные интегрирования, используя независимые и зависимые начальные условия;
подставить в общее решение постоянные интегрирования.
Операторный метод расчёта:
составить операторную схему замещения;
используя любой из методов расчёта установившихся режимов в линейных электрических цепях, найти требуемое изображение тока или падения напряжения;
по формуле разложения найти оригинал тока или падения напряжения.
Построение графика переходного процесса:
определить постоянные времени переходного процесса;
определить время переходного процесса, используя постоянные времени переходного процесса;
нарисовать результирующий график как сумму графика принуждённой составляющей и графика (-ов) свободной составляющей тока или падения напряжения.
Моделирование в среде Electronicsworkbench:
собрать до коммутационную схему;
подключить осциллограф для регистрации требуемого переходного процесса;
по времени переходного процесса (см. пункт 3) определить масштаб по оси времени осциллографа таким образом, чтобы на экране поместилось примерно двойное время переходного процесса, согласно графику пункта 3 выбрать масштаб по оси ординат на экране осциллографа;
нажать на экране клавишу «пуск», выйти на до коммутационный установившийся режим, сделать коммутацию (замкнуть или разомкнуть ключ), сохранить график переходного процесса.
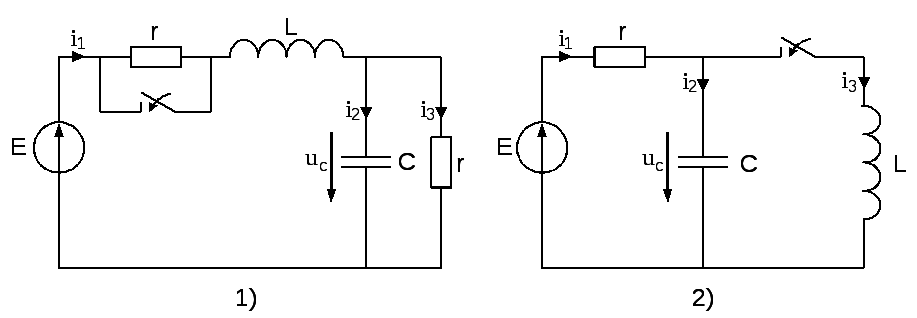
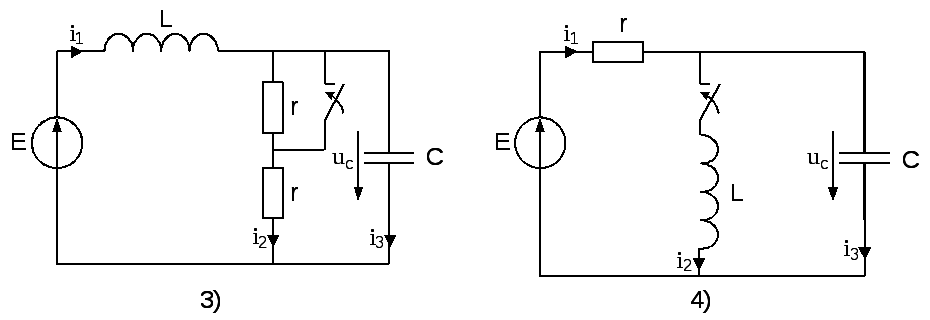
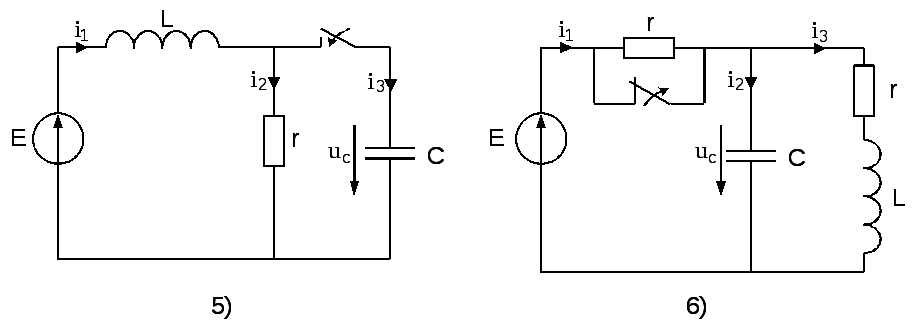
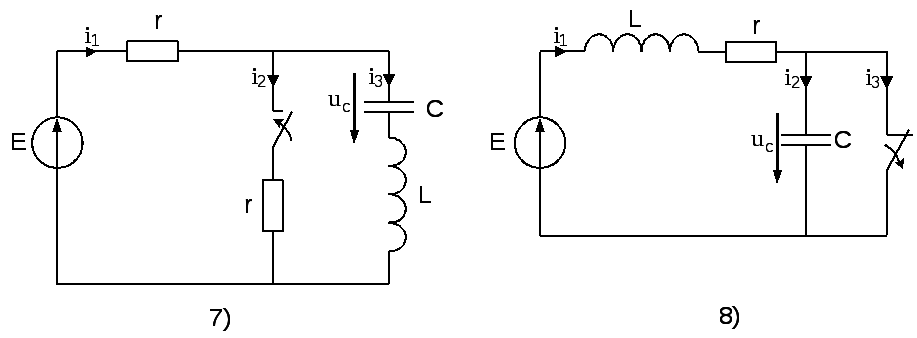
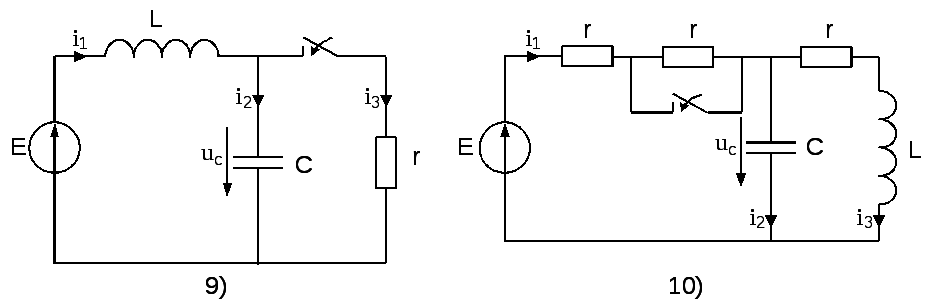
Рис. 6. Десять вариантов схем таблицы 6.
Таблица 6
|
№ варианта |
№ варианта схемы на рис. 6 |
r |
L |
C |
E |
Определить закон изменения |
|
- |
- |
Ом |
Гн |
мкФ |
В |
- |
|
1 |
1 |
10 |
0,1 |
100 |
100 |
uc(t) |
|
2 |
2 |
8 |
0,02 |
31,3 |
150 |
i1(t) |
|
3 |
3 |
6 |
0,06 |
83,3 |
200 |
i2(t) |
|
4 |
4 |
15 |
0,025 |
80 |
110 |
i3(t) |
|
5 |
5 |
48 |
0,06 |
200 |
120 |
i1(t) |
|
6 |
6 |
8 |
0,05 |
100 |
130 |
i2(t) |
|
7 |
7 |
5 |
0,1 |
120 |
140 |
i3(t) |
|
8 |
8 |
10 |
0,08 |
100 |
50 |
uc(t) |
|
9 |
9 |
15 |
0,1 |
40 |
60 |
i1(t) |
Продолжение таблицы 6
|
№ варианта |
№ варианта схемы на рис. 6 |
r |
L |
С |
E
|
Определить закон изменения |
|
- |
- |
Ом |
Гн |
мкФ |
В |
- |
|
10 |
10 |
10 |
0,05 |
50 |
70 |
i2(t) |
|
11 |
1 |
10 |
0,06 |
50 |
80 |
i3(t) |
|
12 |
2 |
6 |
0,025 |
100 |
90 |
uc(t) |
|
13 |
3 |
8 |
0,1 |
83,3 |
100 |
i1(t) |
|
14 |
4 |
10 |
0,05 |
80 |
125 |
i2(t) |
|
15 |
5 |
15 |
0,08 |
120 |
130 |
i3(t) |
|
16 |
6 |
8 |
0,025 |
100 |
135 |
uc(t) |
|
17 |
7 |
5 |
0,1 |
80 |
140 |
i1(t) |
|
18 |
8 |
6 |
0,05 |
31,3 |
145 |
i2(t) |
|
19 |
9 |
48 |
0,06 |
100 |
150 |
i3(t) |
|
20 |
10 |
6 |
0,08 |
40 |
145 |
uc(t) |
|
21 |
1 |
8 |
0,1 |
120 |
175 |
uc(t) |
|
22 |
2 |
5 |
0,05 |
50 |
200 |
i1(t) |
|
23 |
3 |
10 |
0,025 |
80 |
100 |
i2(t) |
|
24 |
4 |
10 |
0,1 |
100 |
150 |
uc(t) |
|
25 |
5 |
48 |
0,08 |
31,3 |
200 |
i1(t) |
|
26 |
6 |
15 |
0,1 |
83,3 |
110 |
i2(t) |
|
27 |
7 |
8 |
0,05 |
100 |
120 |
i3(t) |
|
28 |
8 |
10 |
0,025 |
40 |
130 |
uc(t) |
|
29 |
9 |
15 |
0,1 |
80 |
140 |
i1(t) |
|
30 |
10 |
10 |
0,06 |
50 |
50 |
i2(t) |
|
31 |
1 |
15 |
0,02 |
100 |
60 |
i3(t) |
|
32 |
2 |
6 |
0,025 |
120 |
70 |
uc(t) |
|
33 |
3 |
10 |
0,08 |
200 |
80 |
i1(t) |
|
34 |
4 |
8 |
0,1 |
80 |
90 |
i2(t) |
|
35 |
5 |
15 |
0,06 |
83,3 |
100 |
i3(t) |
|
36 |
6 |
5 |
0,06 |
120 |
125 |
uc(t) |
|
37 |
7 |
48 |
0,1 |
100 |
130 |
i1(t) |
|
38 |
8 |
10 |
0,025 |
50 |
135 |
i2(t) |
|
39 |
9 |
10 |
0,06 |
31,3 |
140 |
i3(t) |
|
40 |
10 |
6 |
0,08 |
50 |
145 |
uc(t) |
|
41 |
1 |
15 |
0,1 |
200 |
150 |
i3(t) |
|
42 |
2 |
8 |
0,1 |
100 |
145 |
i2(t) |
|
43 |
3 |
10 |
0,1 |
120 |
150 |
i3(t) |
|
44 |
4 |
6 |
0,06 |
83,3 |
200 |
uc(t) |
|
45 |
5 |
10 |
0,08 |
50 |
110 |
i1(t) |
Продолжение таблицы 6
|
№ варианта |
№ варианта схемы на рис. 6 |
r
|
L |
С |
E
|
Определить закон изменения |
|
- |
- |
Ом |
Гн |
мкФ |
В |
- |
|
46 |
6 |
8 |
0,05 |
40 |
120 |
i2(t) |
|
47 |
7 |
5 |
0,02 |
31,3 |
130 |
i3(t) |
|
48 |
8 |
10 |
0,02 |
120 |
140 |
uc(t) |
|
49 |
9 |
10 |
0,1 |
80 |
50 |
i1(t) |
|
50 |
10 |
8 |
0,025 |
100 |
60 |
i2(t) |
|
51 |
1 |
15 |
0,05 |
200 |
70 |
i3(t) |
|
52 |
2 |
6 |
0,08 |
200 |
80 |
uc(t) |
|
53 |
3 |
15 |
0,02 |
120 |
90 |
i1(t) |
|
54 |
4 |
10 |
0,06 |
100 |
110 |
i2(t) |
|
55 |
5 |
15 |
0,1 |
83,3 |
120 |
i3(t) |
|
56 |
6 |
48 |
0,025 |
31,3 |
130 |
uc(t) |
|
57 |
7 |
5 |
0,08 |
50 |
140 |
i1(t) |
|
58 |
8 |
8 |
0,02 |
40 |
50 |
i2(t) |
|
59 |
9 |
10 |
0,08 |
100 |
60 |
i3(t) |
|
60 |
10 |
5 |
0,06 |
200 |
70 |
uc(t) |
|
61 |
1 |
8 |
0,1 |
120 |
80 |
i2(t) |
|
62 |
2 |
48 |
0,025 |
31,3 |
90 |
i2(t) |
|
63 |
3 |
8 |
0,06 |
50 |
100 |
i3(t) |
|
64 |
4 |
15 |
0,08 |
120 |
125 |
uc(t) |
|
65 |
5 |
6 |
0,025 |
83,3 |
130 |
i3(t) |
|
66 |
6 |
15 |
0,02 |
31,3 |
135 |
uc(t) |
|
67 |
7 |
48 |
0,1 |
200 |
140 |
i1(t) |
|
68 |
8 |
8 |
0,05 |
120 |
145 |
i2(t) |
|
69 |
9 |
5 |
0,02 |
50 |
150 |
i3(t) |
|
70 |
10 |
6 |
0,08 |
100 |
145 |
uc(t) |
|
71 |
1 |
15 |
0,02 |
40 |
130 |
uc(t) |
|
72 |
2 |
10 |
0,08 |
100 |
140 |
i2(t) |
|
73 |
3 |
8 |
0,05 |
200 |
50 |
i3(t) |
|
74 |
4 |
48 |
0,06 |
31,3 |
60 |
uc(t) |
|
75 |
5 |
10 |
0,02 |
80 |
70 |
i1(t) |
|
76 |
6 |
6 |
0,1 |
40 |
80 |
i2(t) |
|
77 |
7 |
15 |
0,02 |
120 |
90 |
i3(t) |
|
78 |
8 |
10 |
0,08 |
100 |
110 |
uc(t) |
|
79 |
9 |
48 |
0,05 |
50 |
120 |
i1(t) |
|
80 |
10 |
8 |
0,02 |
83,3 |
130 |
i2(t) |
|
81 |
1 |
6 |
0,06 |
200 |
140 |
i3(t) |
Окончание таблицы 6
|
№ варианта |
№ варианта схемы на рис. 6 |
r |
L |
С |
E
|
Определить закон изменения |
|
- |
- |
Ом |
Гн |
мкФ |
В |
- |
|
82 |
2 |
5 |
0,1 |
100 |
50 |
uc(t) |
|
83 |
3 |
10 |
0,02 |
40 |
60 |
i1(t) |
|
84 |
4 |
15 |
0,02 |
50 |
140 |
i2(t) |
|
85 |
5 |
15 |
0,1 |
100 |
145 |
i3(t) |
|
86 |
6 |
15 |
0,05 |
31,3 |
150 |
i2(t) |
|
87 |
7 |
48 |
0,08 |
83,3 |
145 |
i3(t) |
|
88 |
8 |
10 |
0,1 |
80 |
175 |
uc(t) |
|
89 |
9 |
5 |
0,05 |
120 |
200 |
i1(t) |
|
90 |
10 |
8 |
0,025 |
100 |
100 |
i2(t) |
|
91 |
1 |
6 |
0,05 |
200 |
150 |
i3(t) |
|
92 |
2 |
10 |
0,08 |
50 |
200 |
uc(t) |
|
93 |
3 |
6 |
0,1 |
80 |
110 |
i1(t) |
|
94 |
4 |
15 |
0,025 |
200 |
120 |
i2(t) |
|
95 |
5 |
8 |
0,08 |
100 |
130 |
i3(t) |
|
96 |
6 |
48 |
0,06 |
40 |
140 |
uc(t) |
|
97 |
7 |
6 |
0,1 |
80 |
50 |
i1(t) |
|
98 |
8 |
15 |
0,05 |
200 |
60 |
i2(t) |
|
99 |
9 |
48 |
0,025 |
100 |
70 |
i3(t) |
|
100 |
10 |
5 |
0,02 |
120 |
80 |
uc(t) |