10. Интегральная теорема Муавра-Лапласа и условия ее применимости. Функция Лапласа ф(х) и ее свойства. Пример.

Интегральная теорема Муавра-Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число m наступления события А в n независимых испытаниях заключено в пределах от а до b (включительно), при достаточно большом числе n приближенно равна

,

Где - функция (или интеграл вероятностей) Лапласа;

, .

Формула называется интегральной формулой Муавра­Лапласа. Чем больше n, тем точнее эта формула. При выполнении условия npq ≥ 20 интегральная формула , так же как и локальная, дает, как правило, удовлетворительную для практики погрешность вычисления вероятностей.

Функция Ф(х) табулирована (см. табл.). Для применения этой таблицы нужно знать свойства функции:

1. Функция Ф(х) нечетная, Т.е. Ф(-х) = -Ф(х).

2. Функция Ф(х) монотонно возрастающая, причем при х → +∞ Ф(х) → 1 (практически можно считать, что уже при х > 4 Ф(х) ≈ 1).

Пример. В некоторой местности из каждых 100 семей 80 имеют холодильники. Вычислить вероятность того, что от 300 до 360 (включительно) семей из 400 имеют холодильники.

Решение. Применяем интегральную теорему Муавра­Лапласа (npq = 64 ≥ 20). Вначале определим:

,

.

Теперь по формуле , учитывая свойства Ф(х), получим

.

(по табл. Ф(2,50) = 0,9876, Ф(5,0) ≈ 1)

10. Следствия из интегральной теоремы Муавра-Лапласа (с вы­водом). Примеры.

Рассмотрим следствие интегральной теоремы Муавра­Лапласа.

Следствие. Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе n независимых испытаний вероятность того, что:

а) число m наступлений события А отличается от произведения nр не более, чем на величину ε > 0 (по абсолютной величине), т.е. ;

б) частость события А заключена в пределах от α до β (включительно), т.е. , Где ,.

в) частость события А отличается от его вероятности р не более, чем на величину Δ > 0 (по абсолютной величине), т.е. .

□ 1) Неравенство равносильно двойному неравенству пр - Е ~ т ~ пр + Е. Поэтому по интегральной формуле:

.

2) Неравенство равносильно неравенствуa ≤ m ≤ b при a = nα и b = nβ. Заменяя в формулах и,величины а иb полученными выражениями, получим доказываемые формулы и,.

3) Неравенство равносильно неравенству. Заменяя в формуле, получим доказываемую формулу.

Пример. По статистическим данным в среднем 87% новорожденных доживают до 50 лет. Найти вероятность того, что из 1000 новорожденных доля (частость) доживших до 50 лет будет: а) заключена в пределах от 0,9 до 0,95; б) будет отличаться от вероятности этого события не более, чем на 0,04 (по абсолютной величине)?

Решение. а) Вероятность р того, что новорожденный доживет до 50 лет, равна 0,87. Т.к. n = 1000 велико (условие npq = 1000·0,87·0,13 = 113,1 ≥ 20 выполнено), то используем следствие интегральной теоремы Муавра-Лапласа. Вначале определим:

, . Теперь по формуле:

.

Б) По формуле :

. Так как неравенство равносильно неравенству, полученный результат означает, что практически достоверно, что от 0,83 до 0,91 числа новорожденных из 1000 доживут до 50 лет.

10. Понятие «случайная величина» и ее описание. Дискретная случайная величина и ее закон (ряд) распределения. Независимые случайные величины. Примеры.

Под случайной величиной понимается переменная, которая в рез-те испытания в зав-ти от случая принимает одно из возможного множества своих значений (какое именно - заранее не известно).

Примеры случайных величин: 1) число родившихся детей в течение суток в г. Москве; 2) количество бракованных изделий в данной партии; 3) число произведенных выстрелов до первого попадания; 4) дальность полета артиллерийского снаряда; 5) расход электроэнергии на пр-тии за месяц.

Случайная величина называется дискретной (прерывной), если множество ее значений конечное, или бесконечное, но счетное.

Под непрерывной случайной величиной будем понимать величину, бесконечное несчетное множество значений которой - некоторый интервал (конечный или бесконечный) числовой оси.

Так, в приведенных выше примерах 1-3 имеем дискретные случайные величины (в примерах 1 и 2 - с конечным множеством значений; в примере 3 - с бесконечным, но счетным множеством значений); а в примерах 4 и 5 - непрерывные случайные величины.

Определение. Случайной величиной Х называется функция, заданная на множестве элементарных исходов (или в пространстве элементарных событий), т.е. , где где ω - элементарный исход (или элементарное событие, принадлежащее пространству Ω, т.е. .

Для дискретной случайной величины множество возможных значений случайной величины, т.е. функции, конечно или счетно, длянепрерывной - бесконечно и несчетно.

Случайные величины обозначаются прописными буквами латинского алфавита Х,У,Z,..., а их значения - соответствующими строчными буквами х,у,z,....

Определение. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Про случайную величину говорят, что она «распределена» по данному закону распределения или «подчинена» этому закону распределения.

Для дискретной случайной величины закон распределения м.б. задан в виде таблицы, аналитически (в виде формулы) и графически.

Простейшей формой задания закона распределения дискретной случайной величины Х является таблица (матрица), в которой перечислены в порядке возрастания все возможные значения случайной величины и соответствующие их вероятности, т.е.

х1	х2	…	xi	…	хn
p1	p2	…	pi	…	pn

Или.

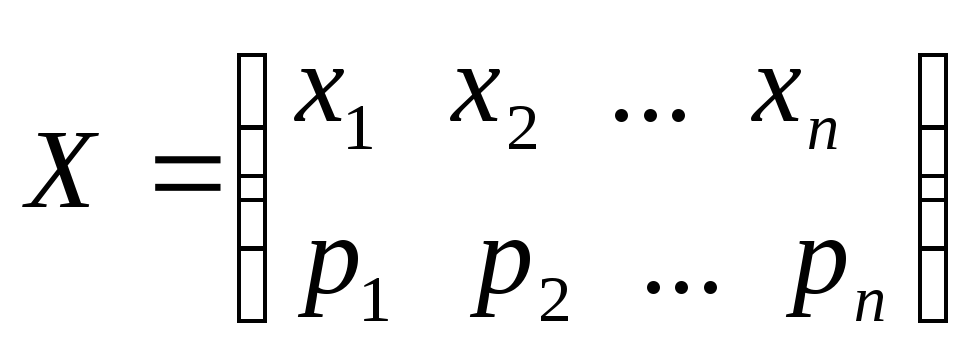Такая таблица называется рядом распределения дискретной случайной величины.

События Х=х₁, Х=x₂,…,Х=x_n, состоящие в том, что в результате испытания случайная величина Х примет соответственно значения х₁, x₂, ..., x_n являются несовместными и единственно возможными (ибо в таблице перечислены все возможные значения случайной величины), Т.е. образуют полную группу. Следовательно, сумма их вероятностей равна 1. Т.о., для любой дискретной случайной величины .

Ряд распределения м.б. изображен графически, если по оси абсцисс откладывать значения случайной величины, а по оси ординат - соответствующие их вероятности. Соединение полученных точек образует ломаную, называемую многоугольником или полигоном распределения вероятностей.

Две случайные величины называются независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина. Так, если дискретная случайная величина Х может принимать значения x_i (i = 1, 2, ..., n), а случайная величина У - значения y_j (j = 1, 2, ..., m), то независимость дискретных случайных величин Х и У означает независимость событий Х = x_i и У = y при любых i = 1, 2, ... , n и j = 1, 2, ..., m. В противном случае случайные величины называются зависимыми.

Например, если имеются билеты двух различных денежных лотерей, то случайные величины Х и Y, выражающие соответственно выигрыш по каждому билету (в денежных единицах), будут независимыми, т.к. при любом выигрыше по билету одной лотереи (например, при Х = x_i) закон распределения выигрыша по другому билету (У) не изменится.

Если же случайные величины Х и У выражают выигрыш по билетам одной денежной лотереи, то в этом случае Х и У являются зависимыми, ибо любой выигрыш по одному билету (Х = x_i) приводит к изменению вероятностей выигрыша по другому билету (У), т.е. к изменению закона распределения У.

10. Математические операции над дискретными случайными ве­личинами и примеры построения законов распределения для КХ,Х'¹, X + К, XV по заданным распределениям независимых случай­ных величин X и У.

Определим математические операции над дискретными случайными величинами.

Пусть даны две случайные величины:

Х:

xi	х1	х2	…	хn
pi	p1	p2	…	pn

У:

уj	y1	y2	…	ym
Pj	p1	p2	…	pm

Произведением kX случайной величины Х на постоянную величину k называется случайная величина, которая принимает значения kx_i с теми же вероятностями р_i (i = 1,2,...,n).

m-й степенью случайной величины Х, т.е. , называется случайная величина, которая принимает значения с теми же вероятностями р_i (i = 1,2,...,n).

Суммой (разностью или произведением) случайных величин Х и У называется случайная величина, которая принимает все возможные значения вида хi+уj (хj-уj или хj·уj), где i = l,2,...,n; j =1,2,...,m, с вероятностями pij того, что случайная величина Х примет значение xi, а у - значение yj:

.

Если случайные величины Х и У независимы, т.е. независимы любые события Х=хi, Y=yj то по теореме умножения вероятностей для независимых событий

.

3амечание. Приведенные выше определения операций над дискретными случайными величинами нуждаются в уточнении: так как в ряде случаев одни и те же значения ,,могут получаться разными способами при различныхxi, yj с вероятностями pi, pij, то вероятности таких повторяющихся значений находятся сложением полученных вероятностей pi или pij.

Вид операции	Выражение знач. Сл\в	Выр знач вер-ти
		не изм-ся
x²	x²	не изм-ся
x+y
xy