10. Ковариация и коэффициент корреляции случайных величин. Связь между екоррелированностью и независимостью случай­ных величин.

Пусть имеется двумерная СВ (Х,Y), распределение которой известно, т.е. известна табл. 5.1 или совместная плотность вероятности . Тогда можно найти математические ожидания М(Х) = а_х, М(Y) = а_у и дисперсии иодномерных составляющих Х иY. Однако математические ожидания и дисперсии случайных величин Х и Y недостаточно полно характеризуют двумерную случайную величину (Х,Y), т.к. не выражают степени зависимости ее составляющих Х и Y эту роль выполняют ковариация и коэффициент корреляции.

Определение. Ковариацией (или корреляционным моментом) К_ху случайных величин Х и Y называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е.

, Или ,

Где ,.

Из определения следует, что . Кроме того,.

т.е. ковариация СВ с самой собой есть ее дисперсия.

Для дискретных случайных величин: .

Для непрерывных случайных величин: .

Ковариация двух случайных величин характеризует как степень зависимости случайных величин, так и их рассеяние вокруг точки . Об этом, в частности, свидетельствуютсвойства ковариации случайных величин.

1. Ковариация двух независимых случайных величин равна нулю.

2. Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий, т.е. , или.

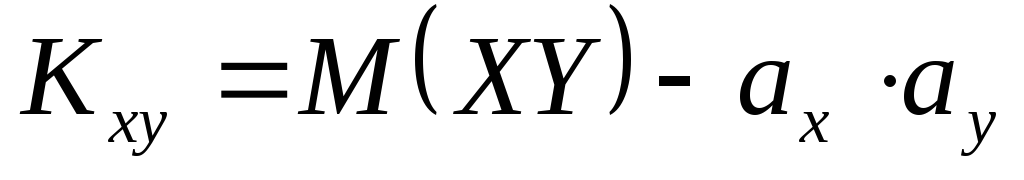3. Ковариация двух случайных величин по абсолютной величине не превосходит произведения их средних квадратических отклонений, т.е. .

Ковариация, как уже отмечено, характеризует не только степень зависимости двух случайных величин, но и их разброс, рассеяние. Кроме того, она - величина размерная, ее размерность определяется произведением размерностей случайных величин. Это затрудняет использование ковариации для оценки степени зависимости для различных случайных величин. Этих недостатков лишен коэффициент корреляции.

Определение. Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратических отклонений этих величин:

.

Из определения следует, что . Очевидно также, что коэффициент корреляции естьбезразмерная величина.

Свойства коэффициента корреляции:

1. Коэффициент корреляции принимает значения на отрезке [-1;1], т.е. .

2. Если случайные величины независимы, то их коэффициент корреляции равен нулю, т.е. .

Случайные величины называются некоррелированными, если их коэффициент корреляции равен нулю. Т.о., из независимости случайных величин следует их некоррелированность. Обратное утверждение, вообще говоря, неверно: из некоррелированности двух случайных величин еще не следует их независимость.

3. Если коэффициент корреляции двух случайных величин равен (по абсолютной величине) единице, то между этими случайными величинами существует линейная функциональная зависимость.

10. Понятие о двумерном нормальном законе распределения. Условные математические ожидания и дисперсии.

Определение. Случайная величина (Х,Y) называется распределенной по двумерному нормальному закону, если ее совместная плотность имеет вид:

Где

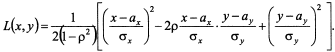
Из определения следует, что двумерный нормальный закон распределения определяется пятью параметрами: .

и аналогично .;

и аналогично .;

.

Т.о., параметры ивыражают математические ожидания случайных величин Х иY, параметры и- их дисперсии, а- коэффициент корреляции между случайными величинами Х иY.

Нетрудно убедиться в том, что каждый из условных законов распределения случайных величин Х и Y является нормальным с условным математическим ожиданием и условной дисперсией, определяемыми по формулам:

, ,

, .

Теорема. Если две нормально распределенные случайные величины Х и Y некоррелированы, то они независимы.

Т.о., для нормально распределенных случайных величин термины «некоррелированность» и «независимость» равносильны.