Лабораторная работа № 129

Изучение динамики поступательного движения твердого тела по наклонной плоскости

Цель работы – экспериментальное определение работы силы трения при скольжении груза по наклонной плоскости.

1. Теоретическая часть

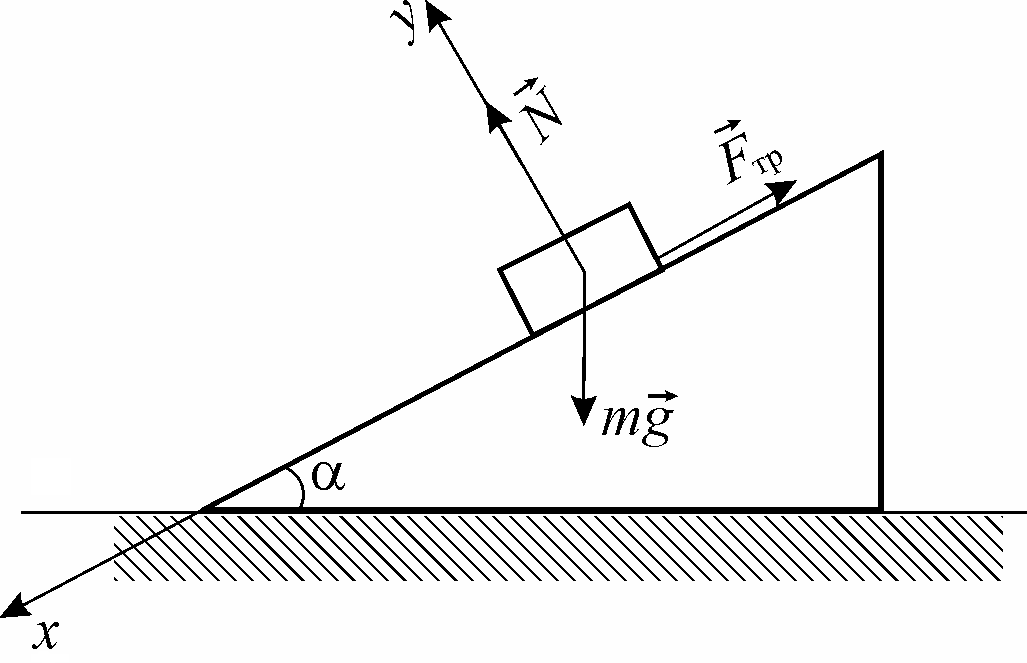
Рис.1. Брусок на наклонной плоскости

На брусок массой m, находящийся на наклонной плоскости, действуют несколько сил (рис.1) – сила тяжести , сила нормальной реакции опорыи сила трения. Под действием этих сил брусок может двигаться или находиться в состоянии покоя.

Рассмотрим сначала состояние покоя, когда равнодействующая всех сил равна нулю:

(1)

где – сила трения покоя. Введем оси координат так, как показано на рис. 1. Посколькуто проекция уравнения (1) на осьдает

Откуда

Т.о. в состоянии покоя сила трения покоя уравновешивает скатывающую силу

Если увеличивать угол наклона то при некотором его предельном значенииэтот баланс нарушится, и брусок начнет соскальзывать с наклонной плоскости. В момент начала соскальзывания сила трения покоя принимает максимальное значение, равное силе трения скольжения

.

По закону Амонтона - Кулона сила трения скольжения по модулю равна

,

где  – коэффициент трения.

Скольжение бруска по наклонной плоскости описывается уравнением динамики

(2)

Проекция уравнения (2) на ось y дает

или

.

Поэтому

.

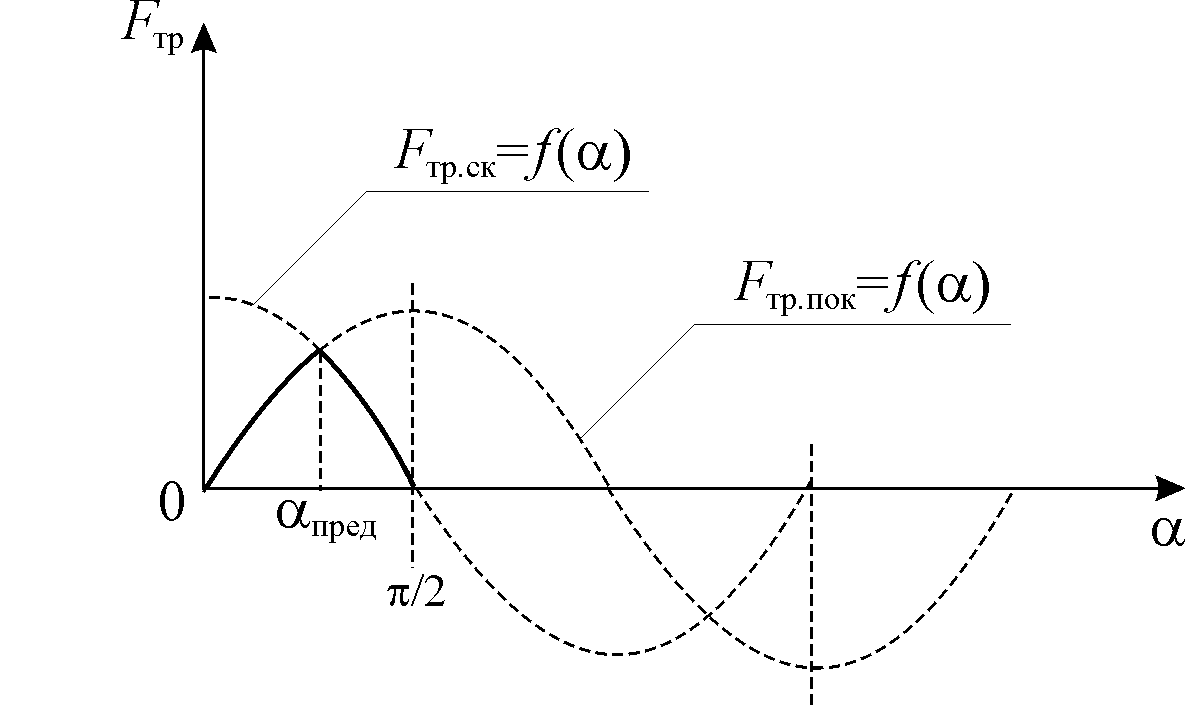На рис.2 показана зависимость сил трения покоя и трения скольжения от угла наклонаКаждая их этих зависимостей имеет свою область определения. Для функцииона лежит в пределах. Область определения функциилежит в интервале. Вне этих областей обе функции не имеют физического смысла.

Рис.2. Зависимости ив функции от угла

Как видно из рис. 2, с ростом угла сила трения покоя изменяется по синусоидальному закону, а сила трения скольжения изменяется по закону косинуса. Пересечение этих двух функций происходит при угле, при достижении которого брусок начнет скользить вниз по наклонной плоскости. Значениенаходится из равенства

,

откуда можно найти коэффициент трения

(3)

Измерив длину пути l бруска по наклонной плоскости и угол ее наклона , можно определить работу силы трения по предельному углуи соответствующему коэффициенту трения

. (4)

Теперь заставим брусок массы m₁ скользить не вниз, а вверх по наклонной плоскости. Для этого (см. рис. 3) привяжем к бруску конец нити, перекинутой через блок; на другом конце нити привяжем груз массы m₂, при опускании которого нить будет тянуть брусок вверх по наклонной плоскости с ускорением а.

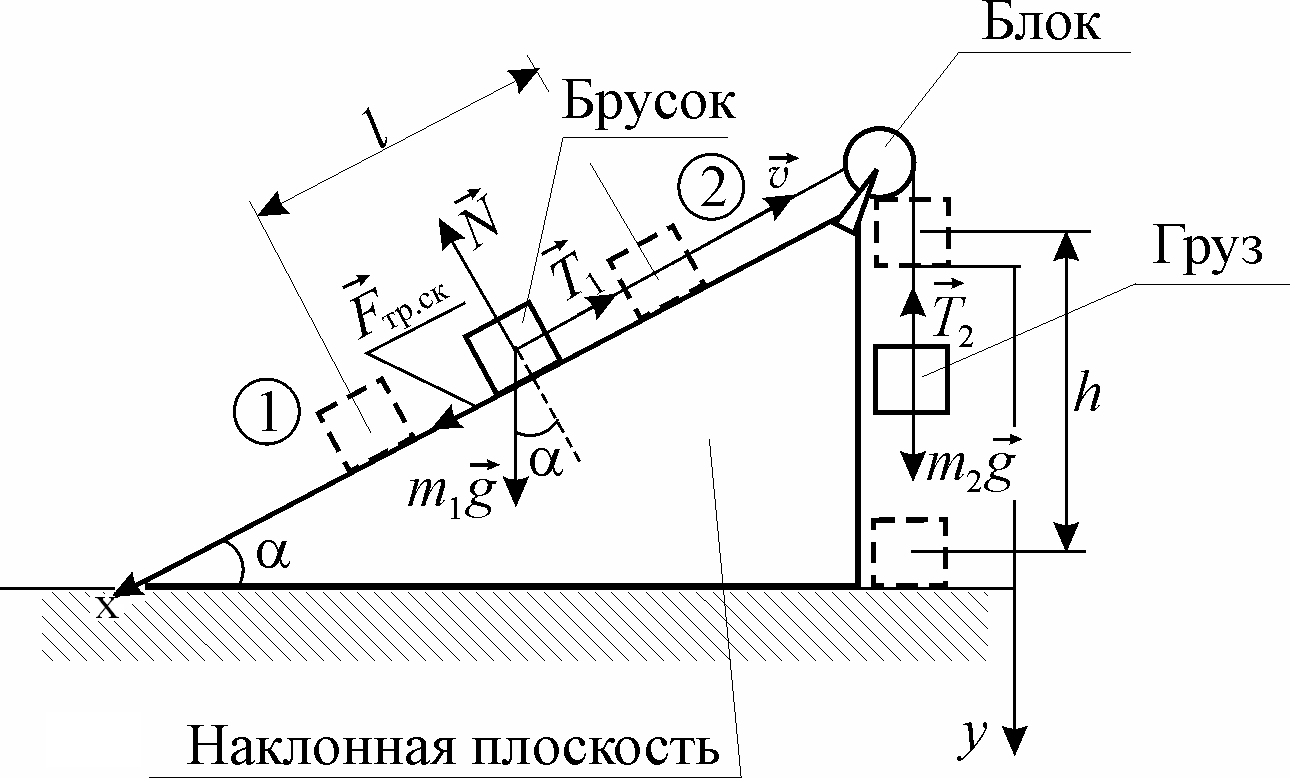
Рис. 3. Схема системы наклонная плоскость – брусок-груз.

На длине пути l вдоль наклонной плоскости (координата ) брусок массойm₁, при перемещении из т. 1- состояния покоя в т. 2 приобретает некоторую скорость и соответственно кинетическую энергиюКинетическая энергия может быть рассчитана как суммарная работа всех сил, приложенных к бруску:

(5)

где

. –работа скатывающей силы,

так как

-работа силы натяжения нити.

Далее будем считать, что нить и блок невесомы, поэтому натяжение нити по обе стороны от блока одинаково: Т₁ = Т₂ = Т. Уравнение движения (второй закон Ньютона) груза m₂ в проекции на ось у дает

откуда имеем значение Т

Высота опускания груза по законам кинематики равна:

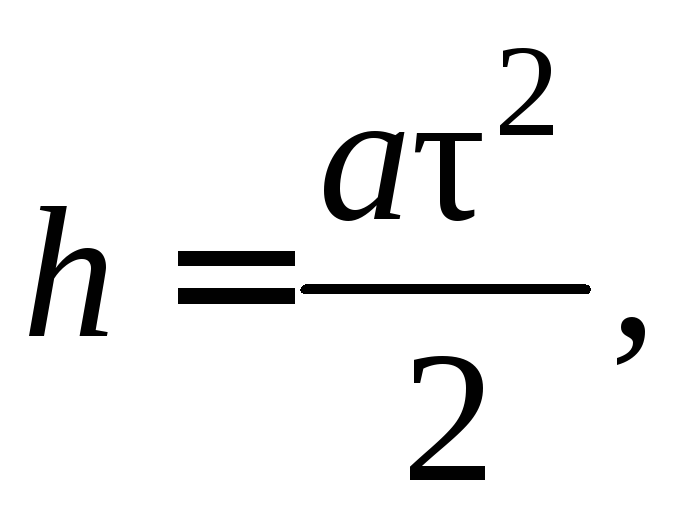
Поэтому ускорение груза можно выразить через измеряемые величины - высоту h и время  спуска груза m₂ -

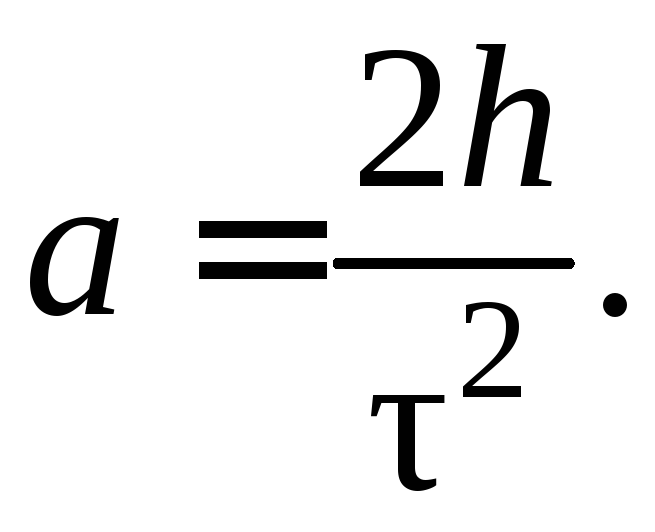
Все тела рассматриваемой системы связаны нерастяжимой нитью и, следовательно, движутся с одинаковой скоростью и ускорением. Поэтому скорость бруска массы m₁ в конце отрезка пути длиной l (положение 2) равна

.

С учетом измеренных и рассчитанных величин уравнение (5) перепишется в виде

,

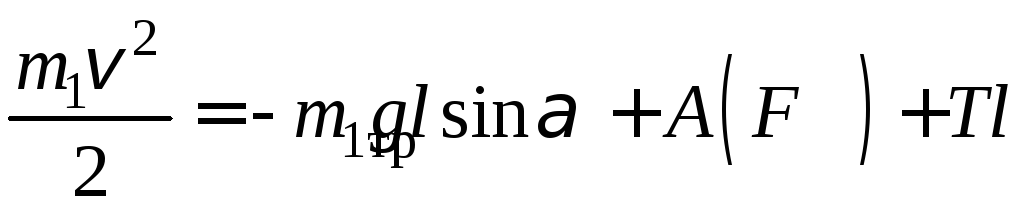или

откуда

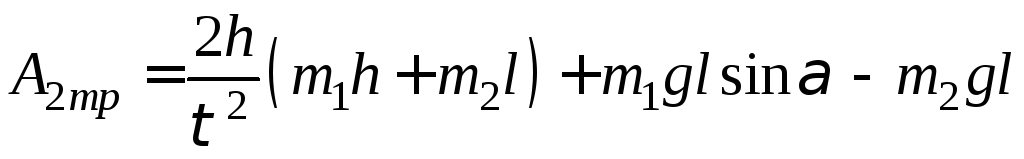. (6)

Учтем, что длина участка 1-2 подъема бруска по наклонной плоскости равна высотеопускания груза (), тогда из (5) получимвыражение для определения работы силы трения по кинематическим параметрам (углу наклона ,длине и времени )перемещения бруска по наклонной плоскости

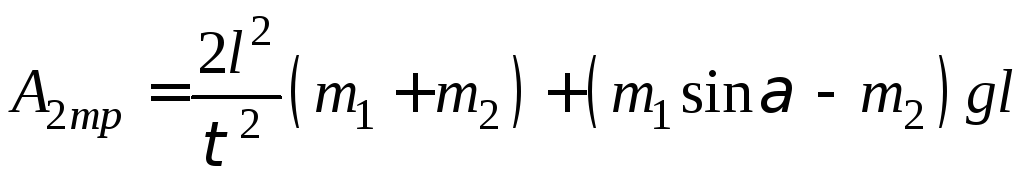. (7)

Приборы и пренадлежности:

1. Лабораторная установка.

2. Набор грузов.