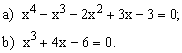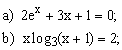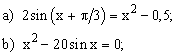контрольная работа по Excel

Вычислите значение выражений при а=15, b=22, c=-6 и сравните с ответом

Выражение:	Ответ:
1)	х1=0,033333
2)	х2=17,10549
3)	х3=-0,185185
4)	х4=0,002381
5)	х5=13,59375
6)	х6=211,7647
7)	х7= -11443329
8) x8=	х8=30
9) x9=	x9=-8665810
10) x10=	x10=1,411877

Задание. Для данной группы продуктов определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.2. На вашем рабочем листе цвет ячеек изменять не нужно):

1. минимальное значение цен в магазинах;

2. максимальное значение цен в магазинах;

3. среднее значение цен в магазинах;

4. количество продуктов, название которых начинается на букву «м»;

5. количество продуктов, название которых начинается на букву «к»;

6. количество продуктов дороже 25 руб.;

7. количество продуктов дешевле 25 руб.;

8. количество продуктов, ассортимент которых обновлялся;

9. ранг продуктов магазина «Рублик» (порядковый номер относительно стоимости друг друга).

Рис. 2. Исходные данные для выполнения лабораторной работы

1. Вычислить:

	, если х кратно 3
	, если х при делении на 3 дает остаток 1
	, в остальных случаях

Даны три целых числа a, b и c. Найти произведение наименьшего и наибольшего из них (например, если заданы числа 4, 3 и 5, то произведение наименьшего и наибольшего из них: 3*5=15). Статистические функции не использовать.

	, если х кратно 5
	, если х при делении на 5 дает остаток 2
	, в остальных случаях

2. Даны три целых числа a, b и c. Найти разность наибольшего и наименьшего из них (например, если заданы числа 4, 3 и 5, то разность наибольшего и наименьшего из них: 5-3=2). Статистические функции не использовать.

Вычислить:

	, если х четное
	, если х при делении на 3 дает остаток больший или равный 1
	, в остальных случаях

Даны три целых числа a, b и c – длины отрезков. Определить вид треугольника, если данные отрезки позволяют его построить.

Абитуриенты поступают в вуз и сдают экзамены по трем предметам. Если общий балл (сумма баллов по трем предметам) выше или равен проходному общему баллу, и у абитуриента не было неудовлетворительных оценок ни по одному предмету (т.е. минимальная оценка по каждому предмету больше, чем 2), то абитуриент считается зачисленным, иначе нет.

1. Создайте и отформатируйте таблицу без заполнения числовыми данными – оценок по предметам. Из текстовых данных внесите название вуза, ФИО абитуриента. Сообщение о зачислении «Не зачислен/зачислен» не вносить – это будет результат работы формулы ячейки G6.

2. Заполните данные по оценкам

3. Выполните подсчет общего балла (функция СУММ).

4. Для заполнения столбца Сообщение о зачислении необходимо проверять два условия, подчеркнутые в постановке задачи (функции ЕСЛИ, И).

5. Поменяв оценки абитуриентов, убедитесь в работоспособности всех ваших формул..

6. Примените шрифтовое оформление, заливку на свое усмотрение.

7. Построить диаграмму Абитуриенты-Оценки по предметам.

«Решение нелинейных уравнений и систем»

1. Задание к лабораторной работе

Задание 1. Найти корни полинома.

№ варианта	Уравнение	Интервал, шаг
1		а) [-1;1], Δx=0,2 b) [-1;1], Δx=0,2
2		а) [-1;4], Δx=0,5 b) [-2;2], Δx=0,5
3		а) [-3;1,5], Δx=0,5 b) [1;2], Δx=0,2
4		а) [-1,8;1,8], Δx=0,3 b) [-1;2], Δx=0,5
5		а) [-2,3;1,2], Δx=0,5 b) [-2,5;1,5], Δx=0,5
6		а) [-1;1], Δx=0,5 b) [-1,5;1], Δx=0,5
7		а) [-1,5; 2,5], Δx=0,5 b) [-1,5;1,5], Δx=0,4
8		а) [-2; 1,5], Δx=0,5 b) [-2;1,5], Δx=0,5
9		а) [-1; 1,5], Δx=0,5 b) [-1;1], Δx=0,2
10		а) [-1,5; 0,5], Δx=0,3 b) [-1,5;1,5], Δx=0,4
11		а) [-1; 3], Δx=0,5 b) [-1;3], Δx=0,4
12		а) [-1,5; 1,5], Δx=0,2 b) [-1;2], Δx=0,2
13		а) [-1,5; 2,5], Δx=0,5 b) [-1,5;1], Δx=0,2
14		а) [-3; 2], Δx=0,2 b) [-2;2], Δx=0,4
15		а) [-4; 1], Δx=0,2 b) [-2;0,5], Δx=0,2

Задание 2. Найти решение нелинейного уравнения. Интервал и шаг изменения аргумента задайте самостоятельно.

№ варианта	Уравнение
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

7