Вариант №1

1. Дана общая задача линейного программирования:

;;

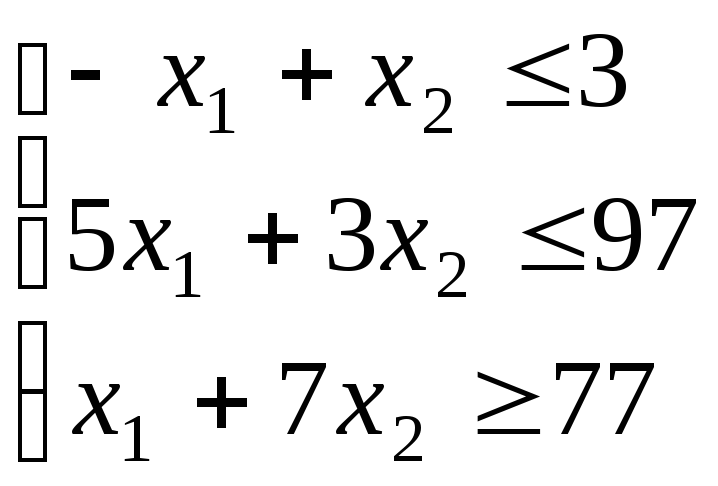1. Построить на плоскости область допустимых решений задачи и геометрически найти максимум и минимум линейной функции цели L(x).

2. Составить М-задачу для максимума и минимума функции цели L(x)и решить ее.

3. Составить двойственные задачи линейного программирования к задачам на максимум и минимум целевой функции.

2. Заданы координаты вершин четырехугольника АВСД: А(-1;2), В(3;5), С(5;7), Д(7;6). Построить на плоскости область допустимых решений задачи и геометри­чески найти минимум линейной функции цели 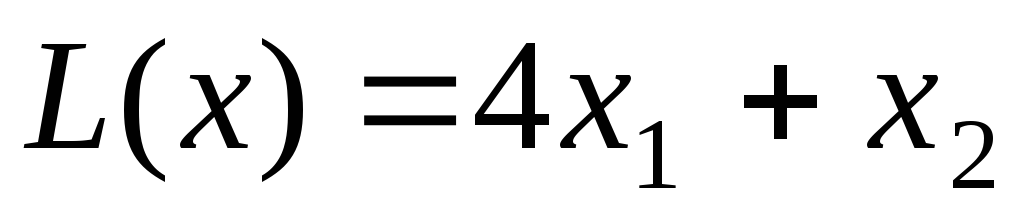_{. Решить задачу линейного программирования симплекс- методом.}

3. Решить транспортную задачу методом потенциалов:

   ai bj	110	70	80	40
   90	2	5	6	1
   160	3	5	7	2
   50	4	2	6	3

4. Дана матрица игры 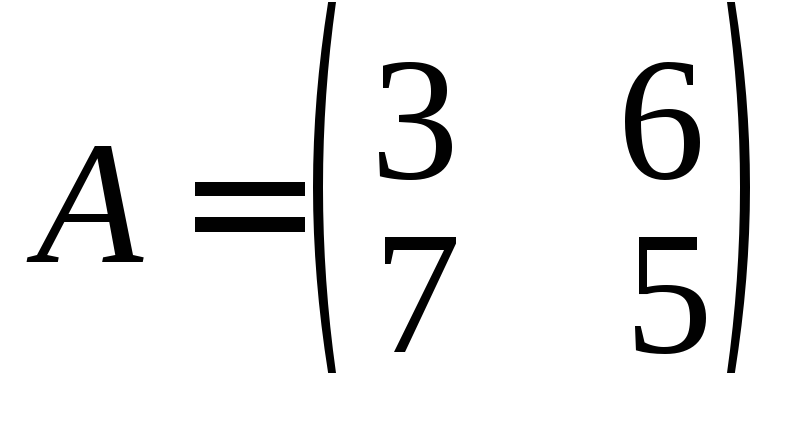. Определить нижнюю и верхнюю цены, если имеется найти седловую точку, составить двойственную пару ЗЛП.

5. Пусть известны возможные значения эффективности на каждом из четырех предприятий отрасли в результате расширения действующих мощностей (табл.)

Капитало вложения (х), д.е.	Прирост выпуска продукции i–го предприятия gi(x), д.е./год
	1	2	3	4
0	0	0	0	0
30	12	17	15	19
60	45	32	38	21
90	55	46	52	56
120	67	62	69	72

Требуется составить план распределения ограниченных капиталовложений по этим предприятиям (К=120 д.е.), максимизирующий общий прирост выпуска при заданной номенклатуре и структуре отраслевого плана производства продукции.

Вариант №2

1. Дана общая задача линейного программирования:

;

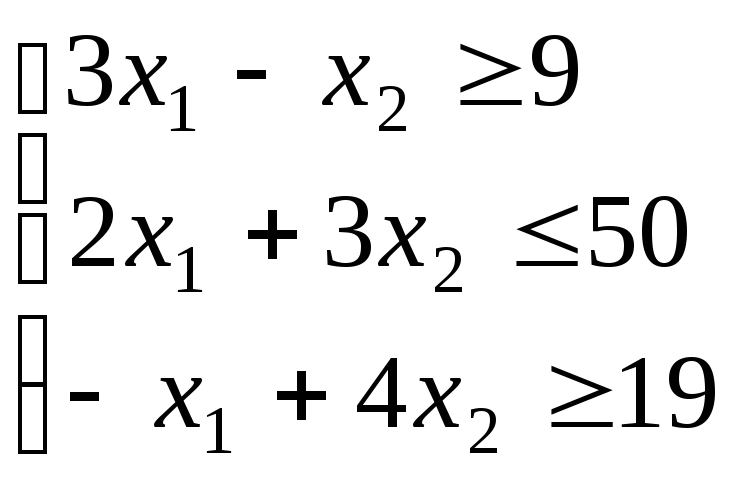
1. Построить на плоскости область допустимых решений задачи и геометрически найти максимум и минимум линейной функции цели L(x).

2. Составить М-задачу для максимума и минимума функции цели L(x)и решить ее.

3. Составить двойственные задачи линейного программирования к задачам на максимум и минимум целевой функции.

2. Заданы координаты вершин треугольника АВС: А(1;2), В(3;6), С(7;6). Построить на плоскости область допустимых решений задачи и геометрически найти минимум линейной функции цели 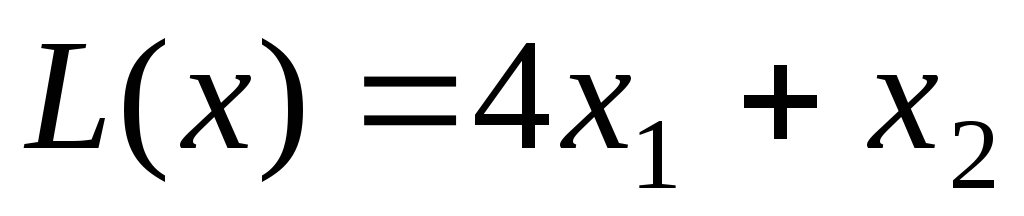_{. Решить задачу линейного программирования симплекс- методом.}

3. Решить транспортную задачу методом потенциалов:

   ai bj	22	21	28	14	16
   39	2	5	6	1	4
   36	3	5	7	5	2
   38	4	2	6	3	3

4. Дана матрица игры 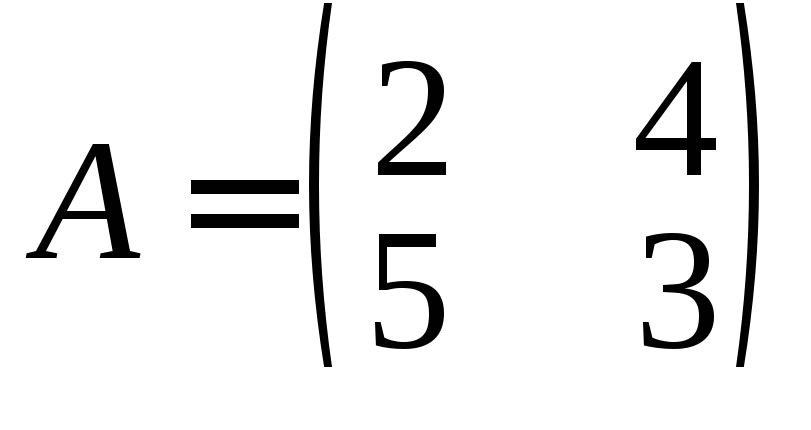. Определить нижнюю и верхнюю цены, если имеется найти седловую точку, составить двойственную пару задач линейного программирования.

2. Пусть известны возможные значения эффективности на каждом из четырех предприятий отрасли в результате расширения действующих мощностей (табл.)

Капитало вложения (х), д.е.	Прирост выпуска продукции i–го предприятия gi(x), д.е./год
	1	2	3	4
0	0	0	0	0
35	22	17	15	19
70	45	32	38	42
105	65	46	52	56
140	87	82	94	72

Требуется составить план распределения ограниченных капиталовложений по этим предприятиям (К=140 д.е.), максимизирующий общий прирост выпуска при заданной номенклатуре и структуре отраслевого плана производства продукции.