Определитель матрицы, свойства определителей
Определителем
(детерминантом)
квадратной матрицы А
n-го
порядка (или определителем n-го
порядка) называется число, которое
обозначается через detA,
А
или |A|,
равное алгебраической сумме n!
слагаемых, каждое из которых представляет
собой произведение n
множителей (элементов матрицы), взятых
по одному и только одному из каждой
строки и столбца, причем знак каждого
множителя определяется четностью
подстановки составленной из первых и
вторых индексов, перемножаемых элементов:
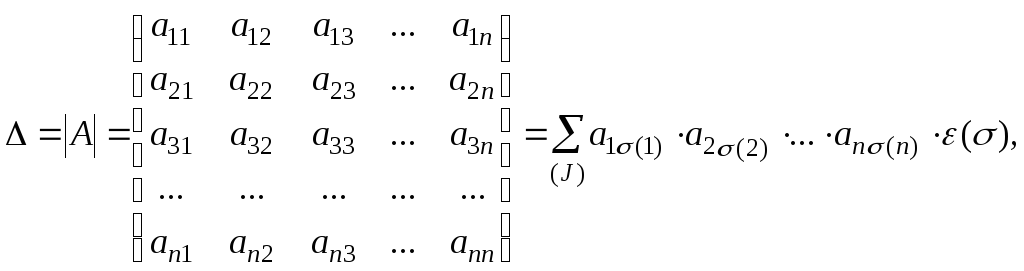
где
- знак перестановки,
,
где
-
число инверсий перестановки:
.
Дадим
понятие инверсии. В перестановке
два числа
и
составляютинверсию,
если i<j,
но
>
.
Рассмотрим определитель второго порядка.
В данном случае имеется две перестановки:
и
.
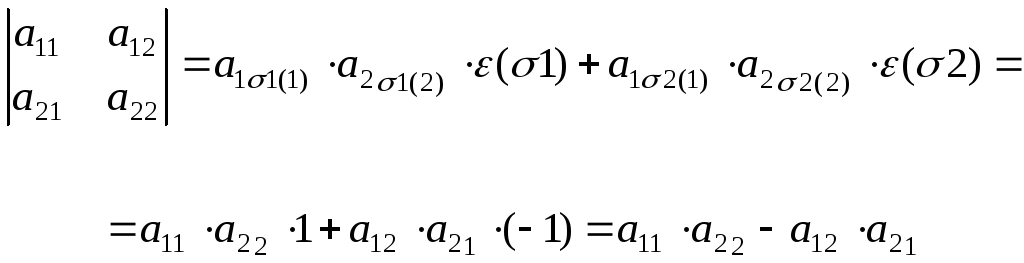
Рассмотрим определитель третьего порядка.
3!=1·2·3=6 Следовательно число инверсий равно шести.
,
,
,
,
,
.
Определитель
третьего порядка вычисляется по формуле:
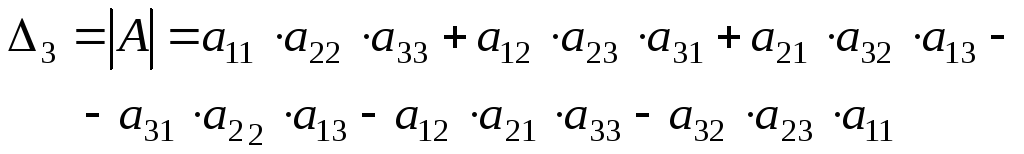(2.1)
Это число представляет алгебраическую сумму, состоящую из 6 слагаемых. В каждое слагаемое входит по одному элементу из каждой строки и каждого столбца матрицы. Знаки, с которыми члены определителя входят в (2.1), легко запомнить, пользуясь схемой (Рис.1), которая называется правилом треугольников или правилом Сарруса
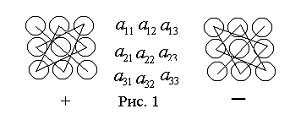
(слева на Рис. 1 дано правило вычисления положительных членов определителя, а справа – отрицательных).
Пример 2.1:
Сосчитаем определители:
;
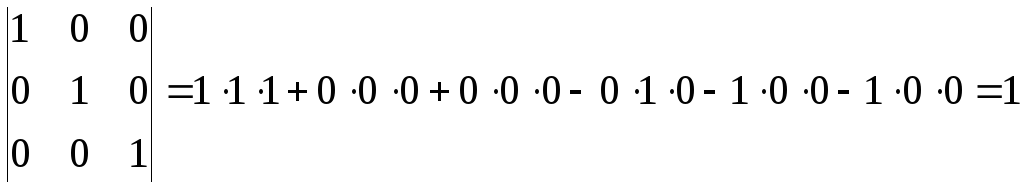
Свойства определителей:
Определитель транспонированной матрицы равен определителю исходной матрицы.
Определитель матрицы, содержащей нулевую строку (столбец), равен нулю.
Общий множитель элементов некоторой строки (столбца) матрицы можно вынести за знак определителя, если этот множитель не нулевой.
Если в матрице поменять местами две строки (столбца), то ее определитель изменит только знак.
Определитель матрицы с двумя одинаковыми строками (столбцами) равен нулю.
Две строки (столбца) матрицы называются пропорциональными, если одна из них получается умножением другой на некоторое отличное от нуля число.
Определитель матрицы с пропорциональными строками равен нулю.
Если к одной строке матрицы прибавить другую ее строку, умноженную на некоторое число, то определитель матрицы не изменится.
Минором Мij элемента aij матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученной из исходной матрицы вычеркиванием i-ой строки и j-го столбца.
Например, минором элемента a12 матрицы третьего порядка будет:
.
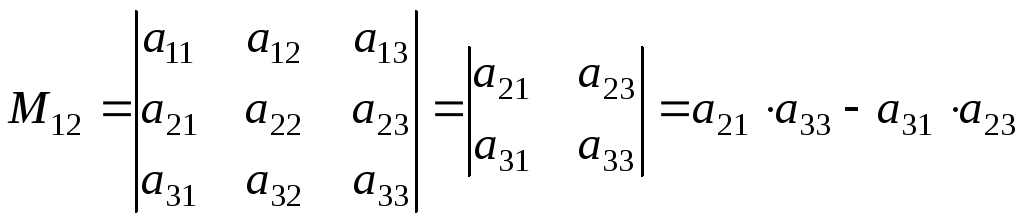
Каждая матрица n-го порядка имеет n2 миноров (n-1) порядка.
Алгебраическим дополнением Aij элемента aij матрицы n-го порядка называется его минор, взятый со знаком (-1)i+j:
Aij=(-1)i+j ·Mij,
т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца (i+j) – четное число, и отличатся от минора знаком, когда (i+j) – нечетное число.
Например,
;
.
Теорема Лапласа Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
(разложение по элементам i-ой строки; i=1;2;…;n),
(разложение по элементам j-го столбца; j=1;2;…;n).
Данное разложение часто используется для нахождения определителя матрицы 4-го порядка.
Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е.
.
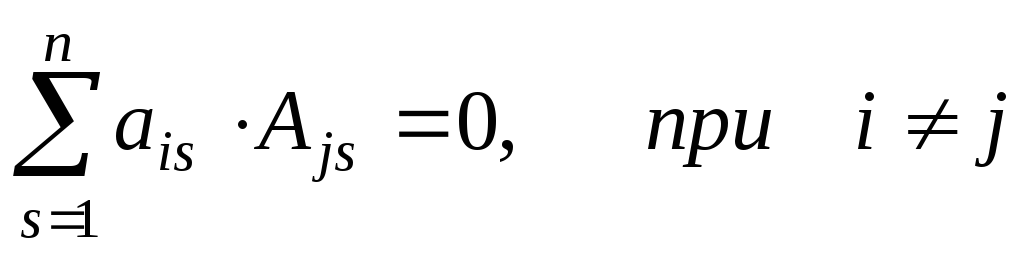Объединяя результат теоремы Лапласа и этого свойства, получаем:
Определитель треугольной матрицы равен произведению диагональных элементов.
Определитель произведения двух квадратных матриц равен произведению их определителей: |C|=|A|·|B|, где С=А·В; А и В – матрицы n-го порядка.