
- •Стохастический факторный анализ (корреляционный анализ, дисперсионный анализ, регрессионный анализ)
- •Однофакторный дисперсионный анализ
- •Решение прикладных задач средствами excel. Инструменты пакета анализа в Microsoft Excel – Дисперсионный анализ
- •Однофакторный дисперсионный анализ
- •Понятие о двухфакторном дисперсионном анализе
Стохастический факторный анализ (корреляционный анализ, дисперсионный анализ, регрессионный анализ)
Дисперсионный анализ – статистический метод, предназначенный для оценки влияния различных факторов на результат эксперимента, для последующего планирования аналогичных экспериментов (а именно для выявления причинно-следственных связи между вариацией факторов и вариацией результативных признаков).
Среди факторов будем различать случайные и неслучайные величины, измеряемые в любой из шкал: интервальной, порядковой или номинальной.
Суть дисперсионного анализа состоит в разложении дисперсии признака на составляющие, обусловленные влиянием конкретных (контролируемых) факторов и остаточную дисперсию, объясняемую неконтролируемым влиянием или случайными обстоятельствами, и проверке гипотез о значимости их влияния.
Модели дисперсионного анализа будем классифицировать:
1) в зависимости от числа факторов на однофакторные, двухфакторные и т.д.;
2) по природе факторов на детерминированные (М1), случайные (М2) и смешанные, в зависимости от того какими являются уровни факторов.
Однофакторный дисперсионный анализ
Пусть имеются т
партий изделий. Из каждой из которых
отобрано соответственно
![]() изделий
(для простоты пусть
изделий
(для простоты пусть![]() ).
Значения показателя качества этих
изделий можно представить в виде матрицы
наблюдений:
).
Значения показателя качества этих
изделий можно представить в виде матрицы
наблюдений:
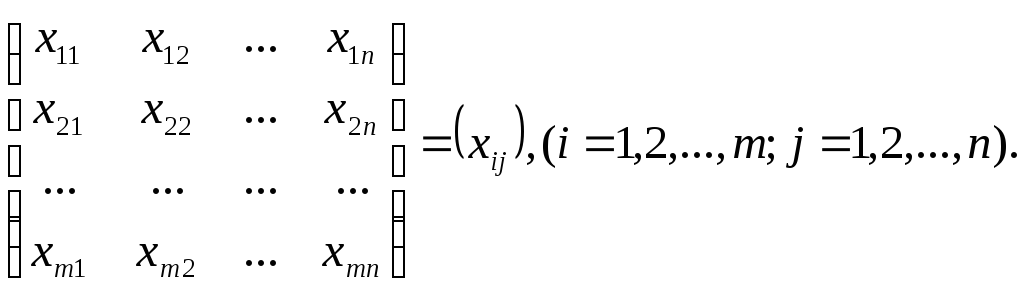
Следует проверить
существенность влияния партии изделий
на их количество. Положим, что элементы
строк матрицы наблюдений – это численные
значения (реализации) случайных величин
![]() ,
выражающих качество изделий и имеющих
нормальный закон распределения с
математическими ожиданиями соответственно
,
выражающих качество изделий и имеющих
нормальный закон распределения с
математическими ожиданиями соответственно![]() и
одинаковыми дисперсиями
и
одинаковыми дисперсиями![]() .
Задача сводится к проверке нулевой
гипотезы
.
Задача сводится к проверке нулевой
гипотезы![]() ,
осуществляемой в дисперсионном анализе.
,
осуществляемой в дисперсионном анализе.
Пусть усреднение по какому-либо индексу будет обозначено через «звездочку» (или точкой) вместо индекса, тогда средний показатель качества изделий i-й партии, или групповая средняя для i-го уровня фактора примет вид:
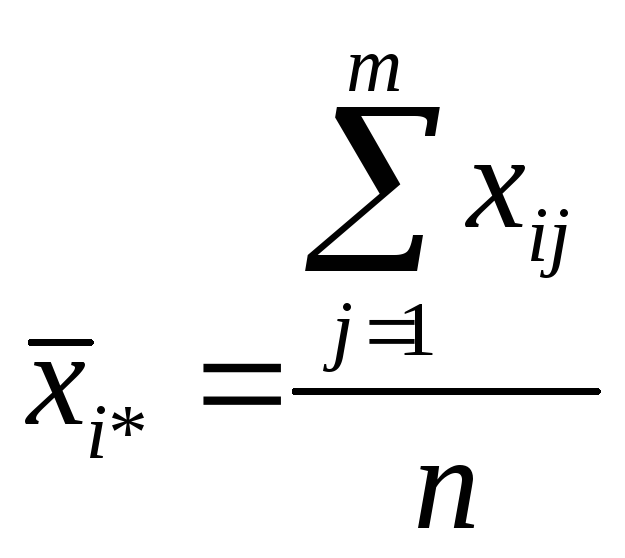 (1)
(1)
а общая средняя –
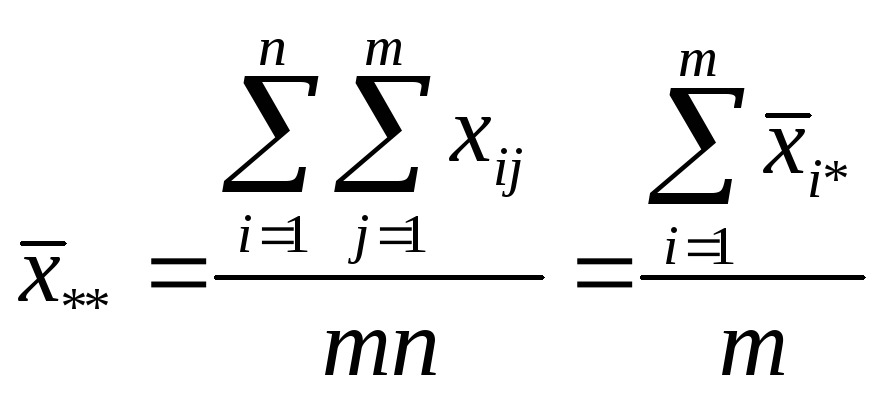 (2)
(2)
Представим схему дисперсионного анализа в виде таблицы:
|
Компоненты дисперсии |
Сумма квадратов |
Число степеней свободы |
Средний квадрат |
|
Межгрупповая |
|
m – 1 |
|
|
Внутригрупповая |
|
m·n – m |
|
|
Общая |
|
m·n – 1 |
– |
Справедливо
следующее тождество:
![]() .
.
В дисперсионном
анализе анализируются не сами суммы
квадратов отклонений, а так называемые
средние квадраты, являющиеся несмещенными
оценками соответствующих дисперсий,
которые получаются деление сумм квадратов
отклонений на соответствующее число
степеней свободы. {Для расчета среднего
квадрата
![]() используютсят
групповых средних, связанных одним
уравнением (2),
Поэтому число степеней свободы:
используютсят
групповых средних, связанных одним
уравнением (2),
Поэтому число степеней свободы:
![]() .
Для расчета
.
Для расчета![]() используютсятn
наблюдений, связанных между собой т
уравнениями (1),
– число степеней свободы:
используютсятn
наблюдений, связанных между собой т
уравнениями (1),
– число степеней свободы:
![]() }.
}.
Проверка нулевой
гипотезы сводится к проверке существенности
различия несмещенных выборочных оценок
![]() и
и![]() дисперсии
дисперсии![]() .
.
Гипотеза Н0
отвергается, если фактически
вычисленное значение статистики
![]() больше
критического
больше
критического![]() ,
определенного на уровне значимостиα
при числе степеней свободы
,
определенного на уровне значимостиα
при числе степеней свободы
![]() ,
,![]() ,
и принимается, если
,
и принимается, если![]() .
.
Применительно к данной задаче опровержение гипотезы Н0 означает наличие существенных различий в качестве изделий различных партий на рассматриваемом уровне значимости.
Задача 1
При исследовании влияния стажа работы на производительность труда (количество деталей в день) в одном из цехов завода получен следующий однофакторный дисперсионный комплекс (таблица А1):
Таблица А1
|
Номер наблюдения |
Стаж работы рабочих (лет) | ||||||||||
|
|
До 5 |
5-10 |
10-15 |
15-20 | |||||||
|
1 |
155 |
154 |
153 |
164 | |||||||
|
2 |
153 |
158 |
162 |
162 | |||||||
|
3 |
149 |
157 |
164 |
163 | |||||||
|
4 |
150 |
161 |
163 |
| |||||||
|
5 |
|
|
167 |
| |||||||
|
|
ИТОГИ |
|
|
|
|
|
| ||||
|
|
Группы |
Счет |
Сумма |
Среднее |
Дисперсия |
|
| ||||
|
|
Столбец 1 |
4 |
607 |
151,75 |
7,583333333 |
|
| ||||
|
|
Столбец 2 |
4 |
630 |
157,5 |
8,333333333 |
|
| ||||
|
|
Столбец 3 |
5 |
809 |
161,8 |
27,7 |
|
| ||||
|
|
Столбец 4 |
3 |
489 |
163 |
1 |
|
| ||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| ||||
|
|
Дисперсионный анализ |
|
|
|
|
| |||||
|
|
Источник вариации |
SS |
df |
MS |
F |
P-Значение |
F критическое | ||||
|
|
Между группами |
301,3875 |
3 |
100,4625 |
7,50887574 |
0,00432931 |
3,490294821 | ||||
|
|
Внутри групп |
160,55 |
12 |
13,37917 |
|
|
| ||||
|
|
|
|
|
|
|
|
| ||||
|
|
Итого |
461,9375 |
15 |
|
|
|
| ||||
Х**=158,4375
