Правило знаков при изгибе

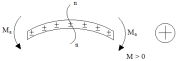
!!!Момент считается «+», если слева от сечения направлен против часовой стрелки, а справа по часовой.

Если балка прогибается выпуклостью вниз, то эпюра моментов будет «+»

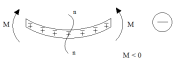
Момент считается «+», если слева от сечения направлен против часовой стрелки, а справа по часовой. Если балка прогибается выпуклостью вниз, то эпюра моментов будет «+»
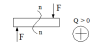
	Поперечная сила Q «+», если эпюра моментов восходящая слева направо.
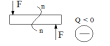
		Поперечная сила Q «-», если эпюра моментов восходящая справа налево.

Зависимость между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки

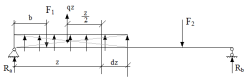
Рассмотрим балку, нагруженную произвольной нагрузкой. Определим поперечную силу в сечении, стоящем от левой опоры на расстоянии . Спроецировав на вертикаль все силы, расположенные левее сечения, получим:

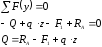
Аналогично вычислим поперечную силу в смежном сечении, расположенном на расстоянии 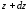от левой опоры:

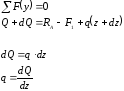
Производная от поперечной силы по абсциссе сечения балки равна интенсивности распределенной нагрузки.

Вычислим теперь изгибающий момент в сечении с абсциссой , взяв сумму моментов сил, приложенных слева от сечения. Для этого распределенную нагрузку на участке длинойзаменим ее равнодействующей, равной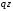и приложенной в середине участка, на расстоянии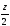от сечения:

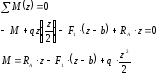
Аналогично вычислим изгибающий момент в смежном сечении, стоящем от левой опоры на расстоянии

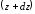
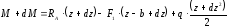(2)

Вычитая из (1) – (2), получим:

т.е. производная от изгибающего момента по абсциссе сечения балки равна поперечной силе (теорема Журавского).

Взяв производную от обеих частей равенства, получим:

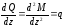
т.е. вторая производная от изгибающего момента по абсциссе сечения балки равна интенсивности распределенной нагрузки.

Все полученные зависимости будем использовать в дальнейшем главным образом при построении эпюр поперечных сил и изгибающих моментов.

Условие прочности по нормальным напряжениям

Для обеспечения прочности балки необходимо, чтобы наибольшие растягивающие и наибольшие сжимающие напряжения при изгибе в опасном сечении, т.е. в сечении, где 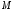имеет наибольшее значение, не превосходили соответствующих допускаемых напряжений:

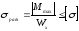
Величина 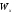называется осевым моментом сопротивления или моментом сопротивления при изгибе.

Значения 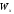для простейших фигур у нас есть в таблицах ГХПС.

Для прокатных сечений (двутавры, швеллера и т.п.) значения 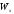указаны в таблицах сортаментов.

Для подбора сечения балки из выше написанного уравнения получим зависимость:

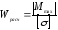
Найдя по этой формуле допускаемый изгибающий момент и зная связь между моментом и нагрузкой (по построенной эпюре моментов) можно определить допускаемую нагрузку.

Условие прочности по касательным напряжениям

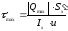- формула Журавского

Закон распределения по сечению касательных напряжений для балки прямоугольного сечения определяются законом изменения 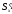, т.к. остальные величины для данного сечения постоянны, причем.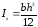

Статический момент относительно оси равен:.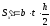

Потенциальная энергия деформации при изгибе

Потенциальную энергию изгиба, равную работе внутренних сил, взятую с обратным знаком, можно определить по формуле:

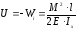
В общем случае изгиба в поперечных сечениях балки кроме изгибающих моментов возникают еще и поперечные силы.

Как показывают исследования поперечная энергия сдвига невелика и ею обычно пренебрегают.

Поэтому данная формула пригодна и для чистого, и для общего случая изгиба.

Лекция № 7

Расчет на прочность.

Метод допускаемых напряжений и разрушающих нагрузок.

1. Допускаемые напряжения.

2. Расчет на прочность по допускаемым напряжениям.

3. Расчет на прочность по разрушающим нагрузкам.

Допускаемые напряжения

В результате испытаний на растяжение (сжатие) можно получить основные данные о механических свойствах материала. Рассмотрим, как можно полученные результаты применить в практических расчетах инженерных конструкций на прочность.

Детали машин и других конструкций должны удовлетворять условиям прочности и жесткости. Размеры деталей необходимо подбирать такими, чтобы под действием приложенных нагрузок они не разрушались и не получали деформаций, превышающих допускаемые. В большинстве деталей машин остаточные деформации, как правило, не допускаются.

Заметные остаточные деформации появляются в пластичных материалах, когда напряжения достигают предела текучести 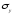. Разрушение наступает, когда напряжения достигают величины предела прочности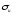; при этом деформации хрупкого материала могут быть незначительными.

Итак, для деталей, изготовленных из пластичного материала, опасным напряжением можно считать предел текучести 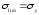; для деталей из хрупкого материала – предел прочности.

Естественно, что эти напряжения не могут быть приняты в качестве допускаемых. Их следует уменьшить настолько, чтобы в эксплуатационных условиях действующие напряжения всегда были меньше предела пропорциональности.

Таким образом, допускаемое напряжение может быть определено по формуле:

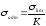
где 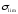- опасное (предельное) напряжение

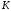- нормативный коэффициент запаса прочности (т.е. предписываемый нормами проектирования и конструирования).

Выбор величины коэффициента запаса прочности зависит от состояния материала (хрупкое или пластичное), характера приложения нагрузки (статическая, динамическая или повторно-переменная) и некоторых общих факторов, имеющих место в той или иной степени во всех случаях.

К этим факторам относятся:

1. Неоднородность материала и, следовательно, различие его механических характеристик в образцах и реальных деталях.

2. Неточность задания величин внешних нагрузок.

3. Приближенность расчетных схем и некоторая приближенность расчетных формул.

4. Учет конкретных условий работы рассчитываемой конструкции.

5. Метод определения напряжений (степень точности этого метода).

6. Долговечность и значимость проектируемого сооружения или машины.

Эти факторы учитывает коэффициент запаса прочности 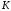, который иногда называют основным.

Коэффициент 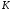определяется опытным путем.

В каждой области техники уже сложились свои традиции, свои требования, свои методы и специфика расчетов, в соответствии с которыми и назначается коэффициент запаса прочности.

Величина нормативного коэффициента запаса прочности регламентируется для строительных конструкций - СНиП, для машиностроительных – внутриотраслевыми заводскими нормами.

Величина запаса прочности зависит от того, какое напряжение считается опасным.

Для пластичных материалов в случае статической нагрузки опасным напряжением, как уже сказано следует считать предел текучести, т.е.

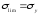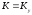, а , тогда:

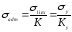
где - коэффициент запаса прочности по отношению к пределу текучести.

На основании данных длительной практики конструирования, расчета и эксплуатации машин и сооружений, величина коэффициента запаса прочност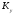и для сталей при статической нагрузке принимается равной.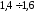

Для хрупких материалов при статических нагрузках опасное напряжение – предел прочности, т.е.

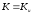, а , тогда: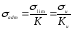

где 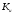- коэффициент запаса прочности по отношению к пределу прочности.

Величину коэффициента запаса прочности для хрупких материалов обычно принимают равной от 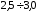. Допускаемые напряжения, получаемые по этой формуле, обычно называют основными допускаемыми напряжениями в связи с тем, что предел прочности определить проще, чем предел текучести.

Поэтому иногда и для пластичных материалов при определении допускаемых напряжений исходят из величины предела прочности, пользуясь формулой:

В этом случае, учитывая, что 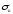превышает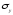на 50-70%, коэффициент запаса прочности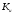для пластичных материалов принимают равным.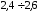

Расчет на прочность по допускаемым напряжениям предполагает выбор нормативного коэффициента запаса прочност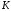и , который выбирается из таблиц, составляемых на основании большого числа экспериментальных исследований.

Однако иногда размеры конструкции или детали уже известны (заданы из эксплуатационных или других требований).

В этом случае расчетным путем определяют фактический коэффициент запаса прочности 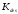. Для этого рассчитывают в опасном сечении детали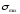

и, зная для материала детали предельное напряжение 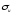или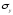, определяют фактический коэффициент запаса:

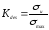- для хрупких материалов

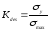- для пластичных материалов

Затем расчетный и нормативный коэффициенты сравнивают между собой, и дается заключение о работоспособности конструкции.

Выбор величины допускаемых напряжений очень важен, т.к. от правильного установления их значений зависят прочность и безопасность проектируемых конструкций, а также экономичность расчета.

Ориентировочные величины основных допускаемых напряжений, принятые в настоящее время для наиболее распространенных материалов, приводятся в справочной литературе.

Конечной целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальных затратах материала.