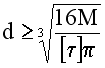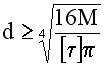Расчет балок на прочность
1550238
В точке 1
поперечного сечения А-А балки...
нет напряжений
д
ействует
нормальное напряжение
действуют нормальное
и касательное
напряжениядействует касательное напряжение
1550239
В точке 1
поперечного сечения А-А балки...
н
ет
напряженийдействует нормальное напряжение
действует касательное напряжение
действуют нормальное
и
касательное
напряжения
1550241
В точке 1
поперечного сечения А-А балки...
нет напряжений
действуют нормальное
и
касательное
напряженияд
ействует
нормальное напряжение
действует касательное напряжение
1550243
В точке 1
поперечного сечения А-А балки...
н
ет
напряженийдействует нормальное напряжение
действуют нормальное
и
касательное
напряжениядействует касательное напряжение
Расчет на жесткость при кручении
1550116
Относительный
угол закручивания стержня равен…
1550124
Пусть G
– модуль сдвига, 
–
допускаемый относительный угол
закручивания.
Тогда
допускаемое значение полярного момента
инерции поперечного сечения удовлетворяет
неравенству…
1550125
Пусть 
–
жесткость поперечного сечения на
кручение.
Тогда
максимальный относительный угол
закручивания равен…
1550126
Пусть угол
поворота сечения С равен «
».
Тогда
величина момента М вычисляется по
формуле…
Расчет на прочность при кручении
1550105
Максимальные
касательные напряжения в поперечном
сечении стержня равны…
1550108
Условие
прочности для стержня имеет вид…
1550109
Если
–
допускаемое касательное напряжение,
то из расчета на прочность диаметр
вала…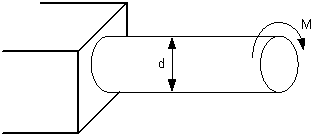
1550112
Если
–
допускаемое касательное напряжение,
то из расчета на прочность скручивающий
момент…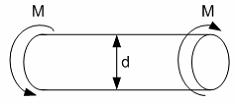
Расчеты стержней на прочность и жесткость
1550072
Проверку на
прочность стержня ВС, имеющего разные
допускаемые напряжения на растяжение
и
сжатие
,
проводят по формуле…
1550075
Проверку
на прочность стержня АВ, имеющего разные
допускаемые напряжения на растяжение
и
сжатие
,
проводят по формуле…
1550080
Если
стержень ВС одинаково работает на
растяжение и сжатие, то проверку на
жесткость проводят по условию…
1550082
Если
стержень ВС одинаково работает на
растяжение и сжатие, то проверку прочности
проводят по условию…
Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
1550347 Критическим напряжением называется напряжение, возникающее в поперечном сечении сжатого стержня при воздействии нагрузки, вызывающей…
п
отерю
устойчивости стержняпоявление в стержне пластических деформаций
появление деформаций, равных допустимому значению
появление деформаций, превышающих допустимое значение
1550349
Для
показанного на рисунке способа закрепления
стержня коэффициент приведенной длины
при вычислении критической силы по
формуле Эйлера равен …
1550350
Для
показанного
на рисунке способа закрепления стержня
коэффициент приведенной длины при
вычислении критической силы по формуле
Эйлера равен …
1550354 Упругое равновесие сжатого стержня устойчиво, если стержень…
изгибается в произвольной плоскости
п
ри
любом малом отклонении от состояния
равновесия стремится возвратиться к
первоначальному состоянию после снятия
воздействия, вызывающего это отклонениепродолжает деформироваться в направлении вызванного малого отклонения
находится в безразличном равновесии: может сохранять прямолинейную форму упругого равновесия, но может и потерять её от малейшего воздействия