1,2,3,4,5,6,7,8,9 ДЕ по сопромату в 2003 Ворде

Угол поворота

Вертикальное перемещение

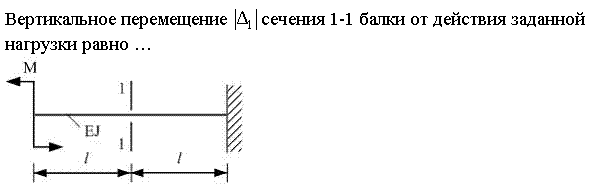
Угол поворота конца консоли

Жесткий брус, нагруженный сосредоточенным моментом

Эпюра изгибающих моментов, построенная на сжатых волокнах, для балки имеет вид

При нагружнии балки прямоугольного поперечного сечения высотой

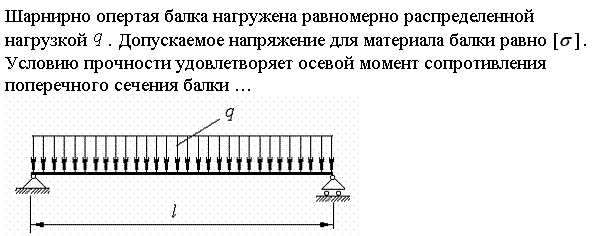
Шарнирно опертая балка нагружена равномерно распределенной нагрузкой

На рисунке показана форма деформированной оси балки

Жесткий брус, нагруженный силой Р, поддерживается в горизонтальном положении

Эпюра изгибающих моментов

При нагружении балки прямоугольного поперечного сечения высотой

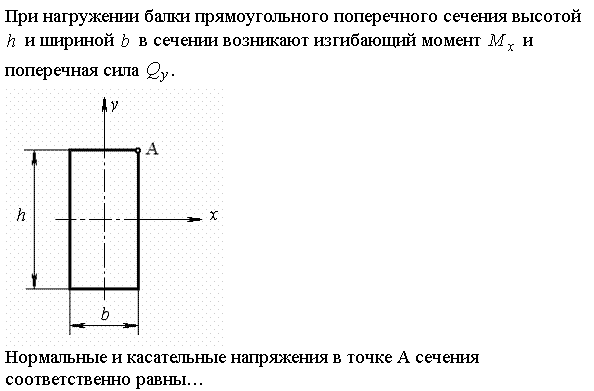
Балка прямоугольного сечения нагружена усилием

Шарнирно опертая балка нагружена сосредоточенным моментом

Консольная балка нагружена сосредоточенной силой

Изгибающий момент

Жесткий брус, нагруженный силой

Угол

Консольная балка нагружена сосредоточенный моментом

Если первую часть стрежня отбросить, то в точке 1

Перемещение центра тяжести сечения по направлению

При чистом изгибе реализуется

Поперечная сила Q, действующая в сечении 1-1, равна…

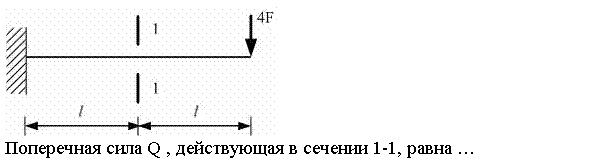
При отбрасывании левой части стержня, в точке 1 сечения С-С будут действовать напряжения

В поперечном сечении балки при изгибе могут возникать внутренние силовые факторы

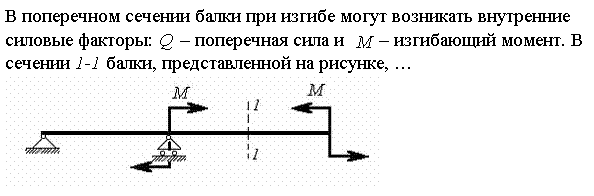
Нормальное напряжение

На рисунке показана схема нагружения балки

Консольная балка нагружена сосредоточенный моментом

Вид (тип) напряженного состояния в окрестности точки К…

При нагружении балки прямоуголльного поперечного сечения высотой

На рисунке показана схема нагружения балки

Пери выводе формулы Эйлера для критической силы сжатого стержня

Стрежень с шарнирно опертыми концами длиной

Признаком потери устойчивости сжатого стержня является..

Остаточной (пластической) деформацией называется деформация

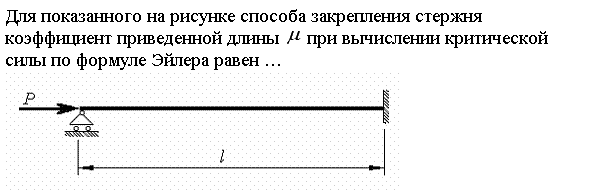
Для показанного на рисунке способа закрепления стержня коэффициент приведенной длины

Стержень, жестко защемленный одним концом

Коэффициент

Дл показанного на рисунке способа закрепления стержня

Стержень длиной

Для сжатого стрежня с шарнирно закрепленными концами

Приведенная на рисунке форма потери устойчивости сжатого стрежня

Стержень с шарнирно пертыми концами

Формула Эйлера для критической силы сжатого стрежня применима, если критическое напряжение

Критической силой сжатого стержня называется

Приведенная на рисунке форма потери устойчивости сжатого стрежня

Приведенная на рисунке форма потери устойчивости сжатого стрежня

Формула Эйлера для критической силы сжатого стержня в виде

Для стержней из малоуглеродистой стали формула Эйлера для критической силы применима

Критическим напряжением называется напряжение, возникающее в поперечном сечении

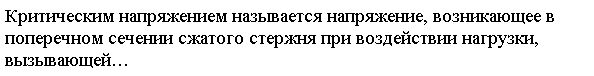
Приведенная на рисунке форма потери устойчивости сжатого стрежня

Стержень, защемленный одним концом

На рисунке показана форма деформированной оси балки

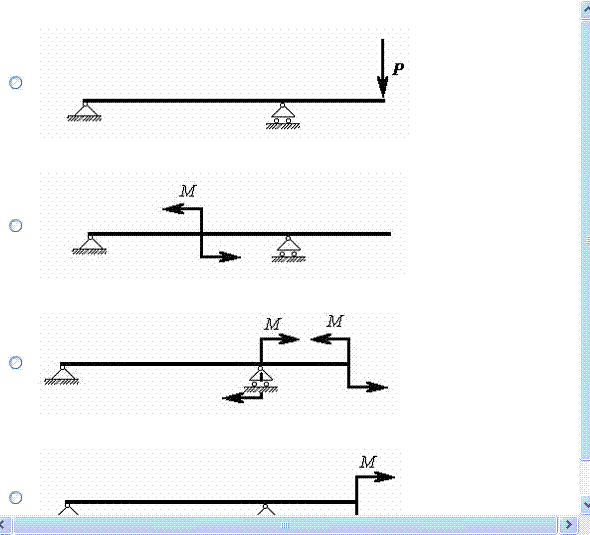
При сжатии упругого стержня

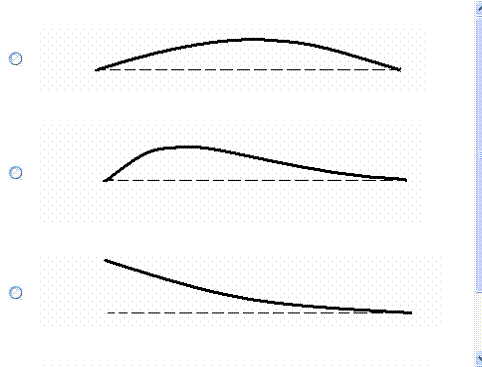
Формулу Ясинского используется при расчетах

Критическая сила сжатого стрежня определяется по формуле

Формула Эйлера для критической силы сжатого стержня

Вывод формулы Эйлера основан на допущении

Условие применимости формулы Эйлера имеет вид

Основным критерием определения критического напряжения

При сжатии упругого стрежня

Для показанного на рисунке способа закрепления стержня

Величина

В формулу Ясинского входит параметр

Для показанного на рисунке способа закрепления стержня

В формуле Эйлера для критической силы сжатого стрежня

При определении критического напряжения на пределом пропорциональности

Приведенная на рисунке форма потери устойчивости сжатого стержня

Для сжатого стрежня с шарнирно закрепленными концами коэффициент

Приведенная на рисунке форма потери устойчивости сжатого стрежня

Стержень, жестко защемленный одним концом

Для показанного на рисунке способа закрепления сткржня

Стержень, защемленный одним концом, длиной

Стержень длиной

Приведенная на рисунке форма потери устойчивости сжатого стержня

Для показанного на рисунке способа закрепления стержня

Стержень с шарнирно опертыми концами длиной

Формула Эйлера для критической силы сжатого стрежня применима,

Коэффициент

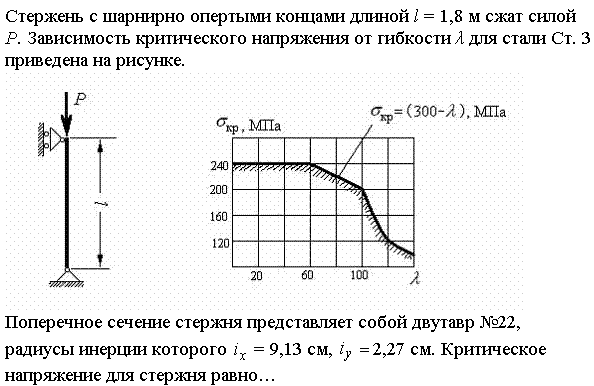
Стержень с шарнирно опертыми концами длиной

Приведенная на рисунке схема потери устойчивости сжатого стержня

Для сжатого стержня с шарнирно закрепленными концами

06_01 Для стержня AB (см. рисунок), видом сложного сопротивления является…

06_02 при известных величинах P,d нормальное напряжение в точке K поперечного сечения стержня равно…

06_03 брус прямоугольного сечения с площадью

06_04 для бруса показанного на рисунке, видом сложного сопротивления является

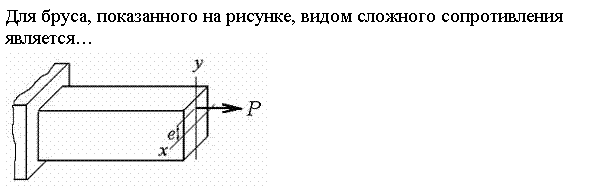
06_07 для бруса, показанного на рисунке, видом сложного сопротивления является

06_05 при известных величинах P,d нормальное напряжение в точке o поперечного сечения стержня равно …

06_06 для бруса прямоугольного поперечного сечения с площадью A и моментами сопротивления

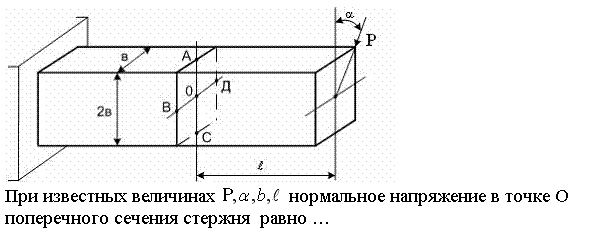
06_08 при известных величинах P,a,b,l нормальное напряжение в точке o поперечного сечения стержня равно …

06_09 балка прямоугольного сечения с моментами сопротивления

06_10 при известных величинах P,d эквивалентное напряжение в точке o в поперечном сечении стержня по теории прочности наибольших касательных напряжений

06_11 для стержня AB круглого поперечного сечения

06_12 изгибающий момент ртносительности оси x

06_13 балка прямоугольного сечения с моментами сопротивления

06_14 стержень круглого сечения с осевым моментом

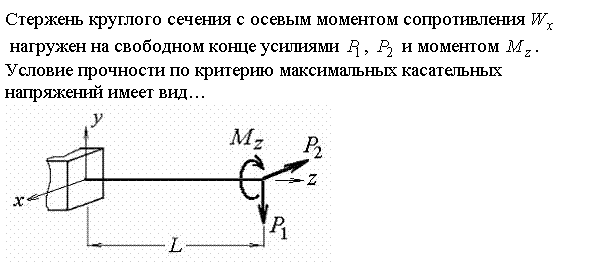
06_15 в случае сложного сопротивления стержня

06_16 допускаемое касательное напряжение для стержня

06_17 вид нагружения стержня

06_24 максимальное нормальное напряжение действует

06_18 стержень испытывает деформацию изгиба

06_19 при известных величинах

06_20 стержень круглого сечения с осевым моментом

06_21 балка прямоугольного сечения с моментами сопротивления

06_25 для нагруженного стержня вид сложного сопротивления

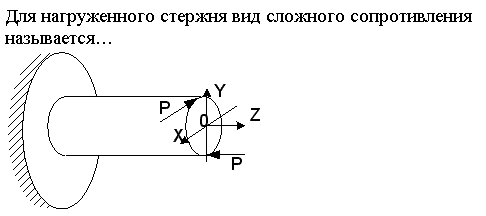
06_27 нейтральной осью поперечного сечения является

06_28 Пусть заданы допускаемое напряжение

06_29 условие прочности для стержня

06_30 опасными точками являются точки

06_31 при сложном напряженном состоянии для оценки

06_32 в сечении A-A наиболее опасными

06_33 для нагруженного стержня вид сложного

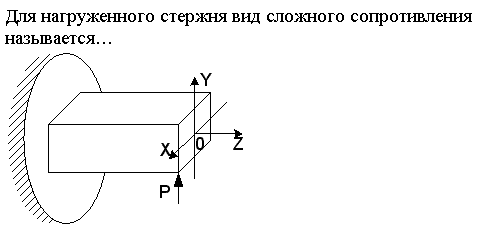
06_34 опасными точками в сечениях A-A являются

06_35 дял нагруженного стержня вид сложности сопротивления

06_36 принцип утверждающий что в точках тела

06_37 условие прочности для опасной точки

06_38 нейтральной осью поперечного сечения

06_39 пусть заданы

06_40 при сложном напряжение состоянии для оценки

06_41неверным утверждением является

06_42 для нагруженного стержня вид сложного сопротивления

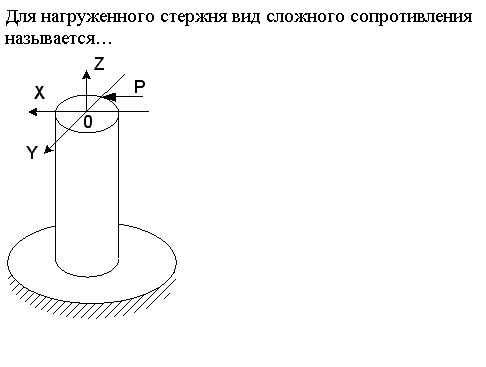
06_43 на схеме изображенной на рисунке наиболее опасной

06_44 вид напряженного состояния в опасных точках при кручении

06_45 условие прочности для стержня

06_47вид напряженного состояния в точке _____

06_01 крутящий момент в сечении 1-1 по абсолютной величине

06.04 для стержня показанного на рисунке видом сложного

06.05 при известных величинах P d нормальное напряжение

13_10 вид напряженного состояния в опасных точках _

16_02 при сложном напряжение состояние для оценки прочности

06.06 для стержня AB видом сложного сопротивления

06.07 балка прямоугольного сечения нагружена усилиями

06.08 брус прямоугольного сечениями с площадью A и моментами сопротивления

06.09 стержень круглого сечения с осевым моментом сопротивления