Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский государственный горный университет

Предмет:

Алгебра и геометрия

Файл:

ЛЕКЦИЯ 2. Уравнения первого порядка ++

.doc

Скачиваний:

Добавлен:

03.06.2015

Размер:

545.79 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

ЛЕКЦИЯ 2

Основные типы обыкновенных дифференциальных уравнений.

Уравнения первого порядка

Обыкновенные дифференциальные уравнения первого порядка. Обыкновенное дифференциальное уравнение первого порядка, не разрешённое относительно производной искомой функции , имеет следующий общий вид:

, (2.1)

где – известная функция. Каждая функция , которая при подстановке в уравнение (2.1) обращает его в тождество, называется решением этого уравнения, а её график – интегральной кривой уравнения (2.1).

Функция называется общим решением уравнения (2.1), если независимо от значения постоянной подстановка этой функции в уравнение (2.1) приводит к тождеству.

Уравнение

называется интегралом дифференциального уравнения (2.1), если каждая функция , определённая этим уравнением и имеющая непрерывную первую производную, является решением уравнения (2.1).

Если можно уравнение (2.1) разрешить относительно производной, то уравнение принимает вид

, (2.2)

где – новая известная функция.

Полагая

это уравнение можно записать в симметрическом виде

Решением этого уравнения называется система таких функций

, ,

где – параметр, что после подстановки в уравнение

За параметр можно принять или , или . Линии, определяемые параметризацией

называются интегральными кривыми уравнения (2.3).

Поле направлений. Пусть в области координатной плоскости задано ОДУ вида (2.2). Так как значения производной – это значения тангенса угла наклона касательной к графику функции (интегральной кривой) в точке графика с координатами , то уравнение (2.2) определяет направления касательных к интегральным кривым в этой точке. Эти направления изображаются отрезками прямых линий, проходящих через точки под соответствующими углами к положительному направлению оси таким образом, чтобы выполнялось условие

Совокупность таких направлений образует поле направлений дифференциального уравнения (2.2) (рисунок 2.1).

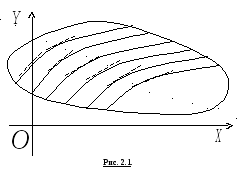
Геометрическое место точек плоскости с одинаковым направлением касательных называется изоклиной. Уравнение изоклины имеет вид:

где – заданный угловой коэффициент.

Теорема существования и единственности решения. Задача Коши (начальная задача) для уравнения (2.2) ставится так: найти решение уравнения

, (2.3)

удовлетворяющее заданному начальному условию

. (2.4)

Геометрический смысл задачи Коши: найти интегральную кривую уравнения (2.2), проходящую через заданную точку .

Имеет место теорема существования и единственности решения задачи Коши (2.3), (2.4).

Теорема 2.1. Пусть в некоторой окрестности точки

выполнены следующие условия:

1) функция непрерывна в каждой точке окрестности как функция двух переменных ;

2) частная производная в каждой точке окрестности ограничена.

Тогда существует единственное решение ОДУ (2.3), определённое в некоторой -окрестности точки

удовлетворяющее начальному условию (2.4), причём это решение единственно.

Пусть в результате интегрирования уравнения (2.3) получается соотношение

. (2.5) Соотношение (2.5) называется общим интегралом ОДУ (2.1), если:

1) при любом выборе значений произвольной постоянной кривая, определённая уравнением (2.5), является интегральной кривой уравнения (2.1);

2) среди множества кривых, определяемых уравнением (2.5), имеются интегральные кривые, удовлетворяющие любым начальным условиям.

Уравнения первого порядка, не содержащие в правой части искомой функции. Эти уравнения имеют следующий вид:

. (2.6)

Уравнение (2.6) является простейшим ОДУ первого порядка. Если – функция, непрерывная на некотором открытом промежутке , то по определению неопределённого интеграла получаем решение уравнения (2.6):

. (2.7)

Это общее решение уравнения (2.6) в области

показанной на рисунке 2.2.

Если интеграл в (2.7) находится в элементарных функциях, то говорят, что уравнение (2.6) интегрируется в элементарных функциях, в противном случае говорят, что это уравнение интегрируется в квадратурах.

Так как первообразная имеет также вид

, (2.8)

где , что проверяется непосредственным дифференцированием

то общее решение, исходя из формул (2.7), (2.8), можно записать в форме Коши:

. (2.9)

Первообразная вида (2.8) называется иногда первообразной Барроу. Если , то

Поэтому формула (2.9) принимает вид

. (2.9')

Это другая форма записи общего решения уравнения (2.6).

Эта же функция (2.9) является и решением задачи Коши

, . (2.10)

Обозначим решение (2.9) так:

. (2.11)

Так, например, решение нулевой задачи Коши

записывается в виде:

Пример 2.2. Найти общее решение уравнения

Выделить решение, удовлетворяющее начальному условию при .

Р е ш е н и е. Так как правая часть уравнения непрерывна при любых , то общее решение записывается, например, по формуле (2.7):

Эта формула определяет бесконечное континуальное семейство парабол.

Пример 2.3. Найти общее решение уравнения

Р е ш е н и е. Находим общее решение по формуле (2.7):

Так как интеграл не находится в элементарных функциях, уравнение интегрируется в квадратурах. Общее решение можно записать и в форме Коши:

Например, для нулевой задачи Коши при , получаем:

Этот интеграл можно для любого вычислить путём численного интегрирования.

Уравнения первого порядка, не содержащие в правой части независимой переменной. Эти уравнения имеют вид:

. (2.12)

Пусть функция непрерывна на промежутке , причём нигде на этом промежутке не принимает нулевого значения, то есть, . Тогда уравнение (2.12) переписывается в виде

. (2.13)

Интегрируя последнее уравнение, получаем:

, (2.14)

или

, (2.15)

где .

Формулы (2.14) или (2.15) дают общий интеграл уравнения (2.12).

Пример 2.4. Решить уравнение

Р е ш е н и е. Так как функция непрерывна при любых и нигде в нуль не обращается, то уравнение перепишем в виде

Интегрируя это уравнение, получаем:

или

Здесь

так как для арктангенса принимается интервал значений

Разрешая общий интеграл относительно , получаем общее решение

где .

Если задано начальное условие , то подставляя и в

общее решение, получаем . Поэтому

().

Уравнения с разделёнными переменными. Уравнение вида

(2.16)

называются уравнением с разделёнными переменными, так как левая и правая части этого уравнения зависят от разных переменных. Пусть и – функции, непрерывные при всех допустимых значениях независимой переменной . Тогда уравнение (2.16) записывается в виде

. (2.17)

В силу равенства (2.17) заключаем, что

. (2.18)

Формула (2.18) даёт общий интеграл уравнения (2.16). В формуле (2.18) значения и берутся из области определения и непрерывности функций и . Вместо формулы (2.18) можно записать общий интеграл уравнения (2.16), используя неопределённые интегралы:

. (2.19)

Решение задачи Коши находится из (2.18), если положить . Действительно, подстановка в (2.18) даёт для произвольной постоянной значение . Следовательно, имеем

. (2.20)

Пример 2.5. Решить уравнение

Р е ш е н и е. Используем формулу (2.19):

Производя интегрирование, получаем

Уравнения с разделяющимися переменными. Уравнения, имеющие вид

, (2.21)

Называются уравнениями с разделяющимися переменными, так как они могут быть приведены к виду уравнений с разделёнными переменными (2.16). Действительно, если все функции в (2.21) непрерывны и то, деля обе части уравнения (2.21) на это произведение, получаем:

. (2.22)

Применяя формулу (2.18), находим общий интеграл уравнения (2.21) в виде

. (2.23)

Формулу общего интеграла (2.23) можно записать, используя неопределённые интегралы:

. (2.24)

Пример 2.6. Найти общий интеграл дифференциального уравнения

Р е ш е н и е. Разделяем переменные:

Используя формулу (2.24), получаем

откуда имеем

где . Потенцируя это равенство, получаем

где произвольная постоянная .

Уравнения с однородной правой частью. Функция нескольких переменных называется однородной функцией степени , если при подстановке в формулу функции произведений имеет место равенство

. (2.25)

В частности, функция двух переменных называется однородной функцией нулевой степени, если выполняется условие

. (2.26)

Положим в (2.26) , тогда

Следовательно, имеем такую цепочку равенств:

. (2.27)

Из (2.27) следует, что всякая однородная функция нулевой степени зависит только от отношения своих аргументов.

Пример 2.7. Функция

является однородной функцией степени . Действительно, подставляя в формулу функции и , получаем:

Определение 2.1. Дифференциальное уравнение вида

, (2.28)

где и – однородные функции одной и той же степени, называется (обыкновенным) дифференциальным уравнение с однородной правой частью.

Перепишем уравнение (2.28) в нормальной форме

. (2.29)

Полагая

перепишем уравнение (2.29) в виде

. (2.30)

Если функция определена и непрерывна на промежутке , функция определена и непрерывна в области, определённой двойным неравенством . Из этого неравенства следует, что