5. РАЗДАТОЧНЫЙ МАТЕРИАЛ по II семестру / Математический анализ. Часть 2 / 1. Лекции / ЛЕКЦИЯ 3. Уравнения высших порядков ++

15

ЛЕКЦИЯ 3

Основные типы обыкновенных дифференциальных уравнений.

Уравнения высших порядков

Основные определения из теории ОДУ высших порядков. Уравнение вида

(3.1)

называется обыкновенным дифференциальным уравнением порядка (ОДУ). Таким образом, порядок дифференциального уравнения – это наивысший порядок входящей в него производной.

Каждая функция , которая при подстановке в уравнение (3.1) обращает его в тождество, называется решением этого уравнения. График решения называется интегральной кривой ОДУ.

Уравнение

(3.2)

Называется интегралом уравнения (3.1), если каждая функция , определённая уравнением (3.2) и имеющая непрерывные производные

,

является решением уравнения (3.2). График функции , определённой уравнением (3.2) также называется интегральной кривой.

Если уравнение (3.1) разрешено относительно старшей производной, то оно имеет вид

, (3.3)

где – известная функция.

Любое ОДУ имеет бесконечное множество решений. Для выделения конкретного решения ставятся начальные условия. Для уравнения (3.3) такие условия имеют следующий вид:

; ; ; . (3.4)

В правых частях (3.4) стоят числа. Смысл задания начальных условий – выделение из бесконечного множества решений ОДУ (3.3) единственного решения, интегральная кривая которого проходит через точку таким образом, чтобы производные в этой точке принимали заданные значения (3.4).

Справедлива следующая важная теорема.

Теорема 3.1. Если функция в правой части уравнения (3.3) непрерывна в некоторой окрестности начальной точки пространства и имеет в этой окрестности непрерывные частные производные по переменным , , , , то уравнение (3.3) имеет и притом единственное решение , удовлетворяющее начальным условиям (3.4).

Решение ОДУ (3.3)

, (3.5)

содержащее произвольных постоянных , называется общим решением уравнения (3.3). Если в общее решение (3.5) подставить конкретные числовые значения постоянных, то получим частное решение ОДУ. Покажем, как из общего решения (3.5) получить частное решение, удовлетворяющее начальным условиям (3.4).

В (3.5) положим и используем первое из условий (3.4), получим

.

Дифференцируя (3.5) по и используя второе из условий (3.4), получаем

.

Производя эти действия до получения производной порядка , получим:

,

.

Приходим к системе уравнений относительно значений произвольных постоянных, удовлетворяющих начальным условиям (3.4):

(3.6)

Если из системы уравнений (3.6) определить значения произвольных постоянных и подставить их в (3.5), то получим частное решение уравнения (3.3), удовлетворяющее начальным условиям (3.4):

. (3.7)

Иногда получить решение в виде (3.7) не удаётся. Пусть в результате интегрирования уравнения (3.3) получается соотношение

. (3.8)

Соотношение (3.8) называется общим интегралом ОДУ (3.3), если:

1) при любом выборе значений произвольных постоянных кривая, определённая уравнением (3.8), является интегральной кривой уравнения (3.3);

2) среди множества кривых, определяемых уравнением (3.8), имеются интегральные кривые, удовлетворяющие любым начальным условиям.

Если решение ОДУ получается в виде одного или нескольких интегралов, то говорят, что это уравнение интегрируется в квадратурах.

Уравнения, не содержащие в правой части искомой функции. ОДУ вида

, (3.9)

где – известная функция, непрерывная на некотором промежутке изменения независимой переменной , не содержит в правой части искомой функции и является простейшим ОДУ порядка . Решение уравнения (3.9) можно найти, последовательно понижая порядок производной.

Действительно, перепишем уравнение (3.9) в виде

и проинтегрируем последнее уравнение один раз, получим:

. (3.10)

Перепишем (3.10) в виде

.

Интегрируя последнее уравнение, получаем

. (3.11)

Интегрируя (3.11), аналогично находим

. (3.12)

Интегрируя (3.12) и продолжая процесс дальше, получаем окончательно:

. (3.13)

Полученная формула (3.13) даёт общее решение уравнения (3.9) в -мерной области, определённой условиями

, , , , .

Уравнение (3.9) можно проинтегрировать и с помощью интегралов с переменным верхним пределом. Цепочка интегрирований имеет вид:

,

,

,

,

. (3.14)

Справедлива формула Дирихле:

. (3.15)

Заменяя в (3.14) первое слагаемое по формуле (3.15), получаем общее решение уравнения (3.9) в виде

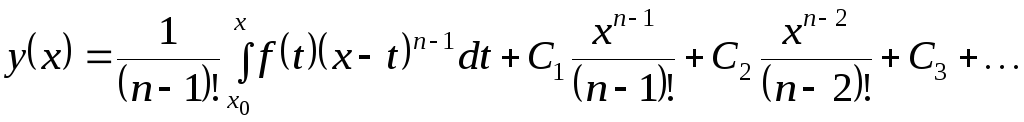
. (3.16)

В формуле (3.16) первое слагаемое – это частное решение уравнения (3.9), удовлетворяющее нулевым начальным условиям: при

, , , .

Отметим, что так как – произвольные постоянные величины, в формулах (3.13) и (3.16) отношения вида можно заменить величинами (умножение произвольной постоянной на любое действительное число, равно как и добавление к ней произвольного числа, не влияет на её “произвольность”).

Пример 3.1. Найти решение ОДУ

,

удовлетворяющее начальным условиям

; ; .

Р е ш е н и е. Непосредственное последовательное интегрирование уравнения с использованием определения неопределённого интеграла даёт:

,

,

.

При получаем:

, , .

Таким образом, частное решение, удовлетворяющее заданным начальным условиям, имеет вид:

.

Пример 3.2. Найти решение ОДУ

.

Р е ш е н и е. Решение этого уравнения находится по формуле (3.13). Цепочка интегрирований имеет вид:

,

,

.

Заменяя (постоянная произвольна), получаем окончательно:

.

Пример 3.3. Найти решение ОДУ

.

Р е ш е н и е. Используем формулу (3.16):

.

Функция

– это частное решение данного уравнения, удовлетворяющее начальным условиям

, .

Уравнения, не содержащие в правой части искомой функции и её последовательных производных до порядка включительно. Такие уравнения имеют вид

, (3.17)

где .

Введём новую переменную, положив

. (3.18)

Тогда

, , .

Теперь уравнение (3.17) примет вид:

. (3.19)

Порядок уравнения понизился на единиц. Если можно найти общее решение уравнения (3.19)

,

то с учётом обозначения (3.18) приходим к уравнению

. (3.20)

Уравнение (3.20) имеет вид (3.9) и для нахождения его решения можно воспользоваться формулой (3.16). Общее решение уравнения (3.17) принимает вид

. (3.21)

Пример 3.4. Найти решение ОДУ

Р е ш е н и е. Уравнение не содержит искомой функции и первой производной . Обозначая , приводим уравнение к виду

.

Интегрируем последнее уравнение:

; ; ;

; ; .

Теперь уравнение сводится к уравнению более низкого порядка:

,

откуда

; .

Общее решение исходного уравнения имеет вид

.

Некоторые понятия теории линейных обыкновенных дифференциальных уравнений высших порядков. Линейный обыкновенный дифференциальный оператор порядка имеет вид

.

(3.22)

Действие оператора (3.22) на функцию определяется формулой:

. (3.23)

В (3.22) и (3.23) коэффициенты – известные функции, непрерывные на промежутке изменения независимой переменной, причём .

Уравнение вида

(3.24)

где – заданная на соответствующем промежутке изменения независимой переменной непрерывная функция, называется линейным неоднородным обыкновенным дифференциальным уравнением порядка , а уравнение

(3.25)

– линейным однородным обыкновенным дифференциальным уравнением порядка , соответствующим неоднородному уравнению (3.24). Запишем уравнения в развёрнутом виде:

, (3.26)

. (3.27)

Общее решение уравнения (3.25) или (3.27) зависит от произвольных постоянных и имеет вид

. (3.28)

Теорема 3.2. Если – любые решения уравнения (3.27), то их линейная комбинация

также является решением этого уравнения при любых значениях коэффициентов линейной комбинации.

Д о к а з а т е л ь с т в о. Доказательство сводится к подстановке в уравнение (3.27) и учёту того, что каждая функция удовлетворяет этому уравнению.

Задача Коши для уравнения (3.24) или (3.26) ставится так: найти решение уравнения (3.26), удовлетворяющее начальным условиям

, , , . (3.29)

Так как уравнение (3.26) является частным случаем общего уравнения (3.3), разрешённого относительно старшей производной, то теорема существования и единственности задачи Коши 3.1 естественным образом распространяется и на случай задачи Коши (3.26), (3.29).

Определение 3.1. Система функций называется линейно зависимой на промежутке (или ), если можно подобрать такие числа , неравные нулю одновременно, что для любых (или ) значение линейной комбинации функций системы с коэффициентами равно нулю:

. (3.30)

Если же таких чисел подобрать нельзя, то есть, условие (3.30) выполняется только в случае, если , то система функций называется линейно независимой на соответствующем промежутке изменения независимой переменной.

Пример 3.5. Система функции линейно независимая, так как многочлен

при неравных одновременно нулю коэффициентах может принять значение равное нулю только в конечном числе точек.

Определение 3.2. Пусть функции на промежутке имеют производные до порядка включительно. Тогда функциональный определитель

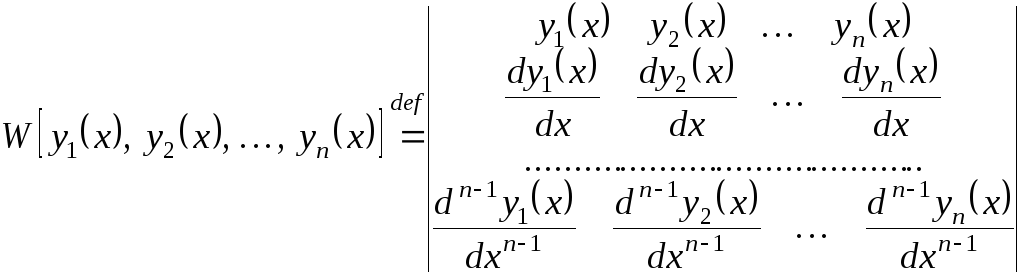
называется определителем Вронского или вронскианом системы функций

.

Теорема 3.3. Если система функций линейно зависима на и все функции системы имеют на этом промежутке ограниченные производные до порядка включительно, то вронскиан системы функций равен нулю в любой точке промежутка .

Д о к а з а т е л ь с т в о. Составим основное тождество

,

где не все коэффициенты равны нулю одновременно. Дифференцируя его раз, получаем СЛАУ относительно неизвестных :

Так эта система линейных алгебраических уравнений однородная с числом неизвестных, равным числу уравнений, то условием её нетривиальной совместности является равенство нулю определителя, который как раз и является определителем Вронского.

Аналогично доказывается и такая теорема.

Теорема 3.4. Если определитель Вронского системы функций

,

определённых на промежутке и имеющих производные до порядка включительно, неравен нулю тождественно на промежутке , то эта система функций линейно независима на .

Справедлива следующая теорема.

Теорема 3.5. Пусть – линейно независимая система частных решений уравнения (3.25) (или (3.27)). Тогда общее решение этого уравнения представляется в виде линейной комбинации

,

где – произвольные постоянные.

Д о к а з а т е л ь с т в о. Доказательство проводится прямой подстановкой линейной комбинации в уравнение (3.25).

Линейно независимая система частных решений уравнения (3.25) или (3.27) называется фундаментальной системой решений этого уравнения.

После этого краткого обзора теории линейных обыкновенных дифференциальных уравнений порядка рассмотрим элементы теории и методы интегрирования линейных обыкновенных дифференциальных уравнений второго порядка с постоянными коэффициентами, которые наиболее часто встречаются на практике.

Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Пусть дано линейное неоднородное дифференциальное уравнение с постоянными коэффициентами второго порядка

,

которое, разделив обе части на , запишем в приведённой форме

, (3.31)

где в уравнении (3.31) введены обозначения:

, , .