5. РАЗДАТОЧНЫЙ МАТЕРИАЛ по II семестру / Математический анализ. Часть 2 / 1. Лекции / ЛЕКЦИЯ 4. Пути и поверхности в пространстве R3

Лемма 8.1. Первая квадратичная форма восстанавливает в касательной плоскости поверхности евклидову метрику (вмещающего) евклидова пространства .

Изометрические поверхности. Среди всевозможных поверхностей особое значение имеют так называемые изгибаемые (изометрические) поверхности. Теория изгибаемых поверхностей сильно развита. Здесь остановимся, однако, только на основных понятиях, касающихся этой теории.

Определение 8.4. Две поверхности и называются изометричными, если между их точками установлено биективное соответствие таким образом, что длина любого, замкнутого пути, соединяющего две фиксированные точки на первой поверхности, совпадает с длиной соответствующего пути на второй поверхности.

Теорема 8.1. Две поверхности и являются изометричными в том и только в том случае, если существуют две такие их параметризации

,

,

что функции совпадают, соответственно, с функциями .

Относительно изометричных поверхностей говорят, что они изгибаемы друг на друга. Так, в пространстве цилиндрическая поверхность, определение которой известно ещё из школьного курса элементарной геометрии, изгибаема на плоскость. Свойства поверхности, выражающиеся через функции , относятся к внутренней геометрии поверхности. Внутренние геометрические свойства поверхности не меняются при всевозможных изгибаниях поверхности. Свойства поверхности, меняющиеся при её изгибаниях, относятся к внешней геометрии поверхности.

Если размерность пространства образов равна , то разделение на внутренние и внешние геометрические свойства не имеет смысла, так как любые два гладких пути изгибаемы друг на друга. Для разделение геометрических свойств на внутренние и внешние уже существенно: цилиндр и плоскость локально изгибаемы друг на друга, а плоскость и сфера нет.

В приложениях декартовые координаты часто обозначают обычным образом, то есть через , а гауссовы координаты через и . Систему параметрических уравнений поверхности (9.2.16) записывают в виде , , , или в векторной форме

.

Для производных текущего вектора поверхности – касательных векторов к гауссовым координатным линиям, вводятся обозначения

,

,

а для коэффициентов первой квадратичной формы – обозначения

, , .

В этих обозначениях первая квадратичная форма поверхности записывается так:

.

Пример 8.1. 1) На координатной плоскости в пространстве за гауссовы координаты (параметры) выберем координаты и . Тогда

; ; ; .

2) Если на координатной плоскости в пространстве за гауссовы координаты выбрать полярные координаты и , то

;

;

;

; ; ;

.

Неявные уравнения поверхности, множества уровня и нормаль. В многомерной дифференциальной геометрии поверхности, размерность которых на единицу меньше размерности вмещающего пространства, называются гиперповерхностями. Размерность гиперповерхности принято обозначать и рассматривать их в пространстве . Таким образом, в рассматриваемом случае поверхности в пространстве размерность поверхности , а размерность пространства .

Параметрические уравнения поверхности запишем в виде

(8.17)

Разрешая первые два уравнения относительно параметров, и подставляя результат в последнее уравнение (8.17), получаем неявное уравнение гиперповерхности в пространстве

, (8.18)

которое можно переписать в виде

. (8.19)

Уравнение (8.18) называется неявным уравнениям поверхности, разрешённым относительно координаты , уравнение (8.19) – неявным уравнением поверхности, неразрешённым относительно координат. Итак, поверхность в пространстве может быть задана также как график функции (8.18) двух переменных, или как множество нулей функции трёх переменных (8.19).

Разрешимость первых двух соотношений нелинейной системы (8.17) следует из теоремы об обратной вектор-функции, которая доказывается в математическом анализе. Здесь ради полноты изложения приведём лишь грубые эвристические соображения.

Рассмотрим первые два из соотношений (8.17):

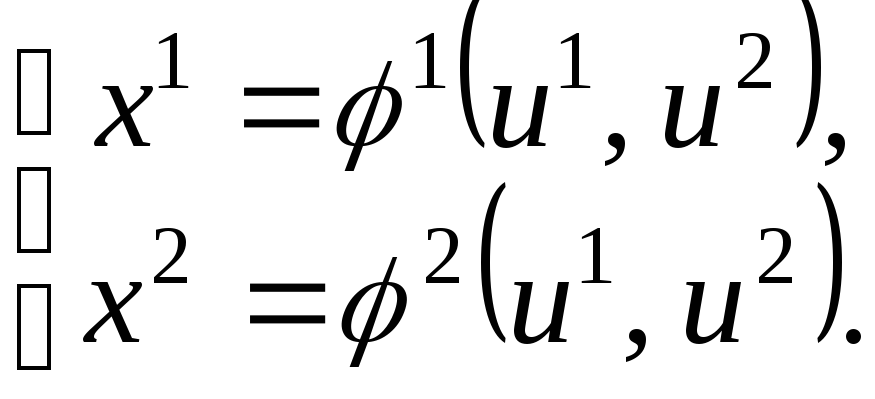
В силу (непрерывной) дифференцируемости функций и справедливы приближённые равенства следующего вида:

,

,

которые перепишем в виде системы линейных алгебраических уравнений:

.

Из линейной алгебры известно, что полученная система однозначно разрешима, если

,

то есть якобиан преобразования (8.17) имеет ранг 2. Находя и , можем подставить их в третье из соотношений (8.17). Очевидно, что разрешимость приведённой системы возможна только в достаточно малой окрестности точки , то есть является локальной.

Определение 8.5. Пусть – функция, задающая поверхность в пространстве посредством уравнения (8.18). Тогда множества

называются множествами уровня функции .

Число из определения 8.5 называется высотой множества уровня, а о самом множестве уровня говорят как о множестве уровня высоты .

Понятия множества уровня и его высоты порождены отношениями между множествами уровня некоторой функции, и её графиком. В соответствии с определением графиком функции называется множество

.

Для функции множество уровня высоты (при ) как раз и является множеством всех точек во множестве определения функции, над которым точки графика функции находятся на высоте . На рисунке 8.1 понятие множества уровня проиллюстрировано на примере функции одного переменного, то есть при .

Множества уровня помогают получить представление о поведении функции на множестве её определения. Часто изучение множеств уровня является единственным наглядным способом изучения функций. Мы, например, в большинстве случаев можем изобразить график функции , а график функции лежит в пространстве и не может быть изображён. Однако множества уровня таких функций являются поверхностями в пространстве и могут быть изображены и, следовательно, дают достаточно удобный способ изучения таких функций. Например, при множества уровня для непостоянных дифференцируемых функций являются гладкими путями в пространстве . Эти пути широко используются в картографии для изображения различных величин, таких как высота неровностей местности. Будем интерпретировать график функции как рельеф некоторой местности. Локальные максимумы графика будем считать возвышениями (горы, холмы и так далее), а локальные минимумы – впадинами. При такой интерпретации можно построить топографическую карту местности, проектируя график функции на плоскость . Тогда все точки на каждой линии уровня (пути в пространстве ) с уравнением соответствуют точкам местности, имеющим высоту над уровнем моря.

Лемма 8.2. В каждой точке 2-мерной поверхности в пространстве градиент функции , задающей поверхность посредством неявного уравнения (8.19), ортогонален касательной плоскости поверхности в этой точке.

Д о к а з а т е л ь с т в о. Зададим произвольный путь, лежащий на поверхности , гладкой параметризацией

, , . (8.20)

Здесь – путь замкнут. Подставляя (8.20) в (8.19), получим

. (8.21)

Для каждой точки пути, соответствующей значению параметра , соотношение (8.21) является тождеством, так как путь лежит на поверхности. Дифференцируя (8.21) по параметру , при получаем:

. (8.22)

В (8.22) входят компоненты вектора-градиента функции (8.19)

,

вычисленные в точке , соответствующей значению параметра , и компоненты касательного вектора пути, вычисленные в той же точке:

.

Из соотношения (8.22) вытекает, что в каждой точке пути, лежащего на поверхности , вектор-градиент ортогонален касательному вектору пути в той же точке . Следовательно, в силу произвольности выбора пути, вектор градиент в каждой точке поверхности ортогонален касательным векторам к гауссовским координатным линиям, то есть, ортогонален касательной плоскости поверхности в точке .

Получим уравнения касательной плоскости поверхности в пространстве , заданной уравнением (8.19). Пусть – точка на поверхности, а – точка на касательной плоскости. Тогда векторы и касательные векторы к координатным гауссовским линиям в точке образуют линейно зависимую систему. Записывая согласно (8.17) вектор в виде

и приравнивая нулю определитель, составленный из компонент системы векторов, получаем уравнение касательной плоскости поверхности:

. (8.23)

Нетрудно видеть, что канонические уравнения нормали поверхности в точке имеют вид:

. (8.24)

Пример 8.2. Написать уравнения касательной плоскости и нормали к поверхности параболоида вращения в точке .

Р е ш е н и е. Имеем . Компоненты вектора градиента в точке

, , .

Уравнения касательной плоскости и нормали имеют, соответственно, вид

, .