5. РАЗДАТОЧНЫЙ МАТЕРИАЛ по II семестру / Математический анализ. Часть 2 / 1. Лекции / ЛЕКЦИЯ 4. Пути и поверхности в пространстве R3

, (6.9)

называется длиной дуги пути .

Теорема 6.4. Функция, введённая формулой (6.9) в определении 6.13, на промежутке непрерывна, монотонно возрастает, причём и . Существует такая нигде непостоянная параметризация пути , что

.

Этим условием параметризация определена единственным образом.

Определение 6.5. Параметризация

,

спрямляемого пути , построенная в теореме 6.4, называется натуральной параметризацией.

Имеет место критерий натуральности параметризация.

Теорема 6.5. Если – гладкая параметризация спрямляемого нигде непостоянного пути , то является натуральной параметризацией в том и только в том случае, если и , то есть, вектор скорости нормирован.

Следствие из теоремы 6.5. Если – натуральная параметризация спрямляемого нигде непостоянного пути , то вектор ускорения ортогонален вектору скорости .

Д о к а з а т е л ь с т в о. По доказанной теореме в любой точке пути , то есть, . Дифференцируя последнее соотношение по , получаем .

Кривизна пути в пространстве . Определим важную величину, характеризующую скорость изменения направления касательной в некоторой фиксированной точке пути . Предположим, что путь является гладким и дважды непрерывно дифференцируемым, то есть его параметризация , определённая координатными функциями, является гладкой и дважды непрерывно дифференцируемой вектор-функцией. Направление касательной к пути в фиксированной точке задаётся вектором скорости, определяемым по формуле (25):

.

В точке , соответствующей на пути значению параметра , вектор скорости равен

.

Угол между векторами скорости пути в точках и , отнесённый к длине дуги пути, может служить мерой искривлённости пути на участке от точки до точки . Эта мера называется средней кривизной параметризованного пути на дуге и с учётом формулы для косинуса угла между векторами

. (7.1)

Формула (7.1) вполне функциональна – все входящие в неё величины легко вычисляются.

Пример 7.1. Вычислить среднюю кривизну окружности (9) радиуса с центром в начале системы координат на участке изменения параметра .

Р е ш е н и е. Из параметрических уравнений окружности имеем:

, , , ,

, .

Так как , то по формуле (7.1) получаем

.

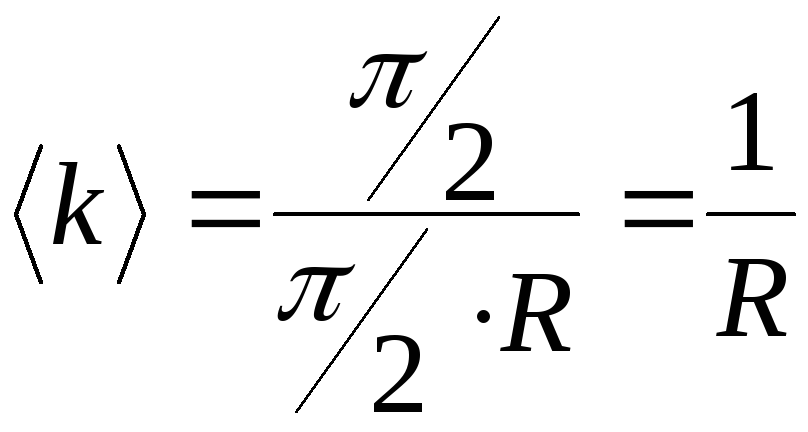Определение 7.1. Кривизной параметризованного пути в точке (соответствующей значению параметра ) называется предел при условии отношения изменения угла между векторами скорости и пути в начальной точке и конечной точке дуги пути к её длине, то есть, предел при условии вдоль пути.

Итак, для вычисления кривизны пути с параметризацией , имеем следующую формулу:

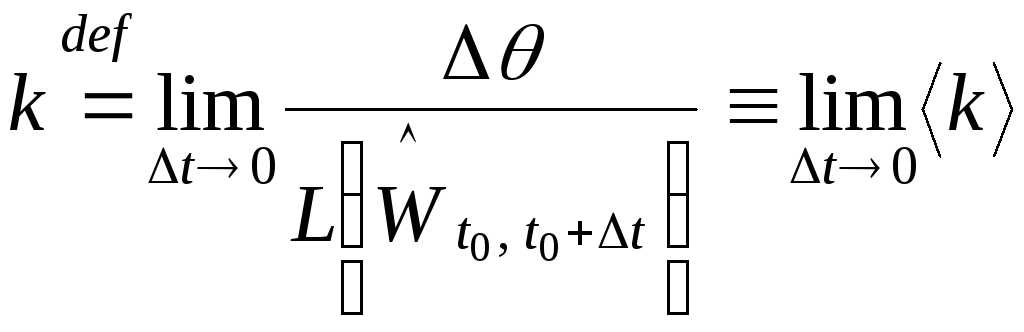. (7.2)

Теорема 7.2. Пусть – нигде непостоянный гладкий путь с дважды непрерывно дифференцируемой параметризацией . Тогда кривизна пути в точке, соответствующей значению параметра , определяется по формуле

. (7.5)

Пример 7.2. Вычислить кривизну окружности, имеющей радиус , в произвольной её точке.

Р е ш е н и е. Воспользуемся формулой (7.5). В координатах, связанных с плоскостью окружности, её параметризация имеет вид:

.

Находя все величины из (7.5), получаем:

, ;

, .

Откуда имеем

.

Таким образом, кривизна окружности равна величине, обратной к её радиусу.

Трёхгранник Френе. В общем случае произвольной параметризации можно построить ортонормированный базис соприкасающегося пространства – так называемый сопровождающий базис Френе (трёхгранник Френе), придерживаясь следующей последовательности действий.

1) Находим систему векторов сопровождающего базиса

и убеждаемся, что она линейно независима.

2) Находим вектор бинормали, вычисляя векторное произведение векторов скорости и ускорения

.

3) Находим вектор главной нормали по формуле

.

4) Нормируем систему векторов .

Плоскость, построенная на векторах трёхгранника Френе, отнесённого к определённой точке пути, является, очевидно, соприкасающейся плоскостью пути в этой точке. Плоскость, построенная на векторах , является, очевидно, нормальной плоскостью пути в соответствующей его точке. Плоскость, построенная на векторах , называется спрямляющей плоскостью пути в соответствующей его точке.

Отображения. Пусть даны два экземпляра и евклидова пространства с ортонормированными базисами и соответственно. Векторы и в этих пространствах представляются в виде разложений и , соответственно. Определим на области функции переменных . Тогда выражение

, (8.1)

при всевозможных значениях переменных задаёт отображение области в пространство , которое обозначим . Сами функции называются компонентами или координатными функциями отображения . Если функции непрерывны, то отображение называется непрерывным; если функции дифференцируемы, то отображение называется дифференцируемым; если функции непрерывно дифференцируемы, то отображение называется непрерывно дифференцируемым.

Можно показать, что из дифференцируемости компонент отображения в некоторой точке следует, что в некоторой окрестности этой точки отображение можно представить в виде

, (8.2)

где – линейный оператор, а – радиус-вектор в , такой, что

.

Соотношение (8.2) также можно принять за определение дифференцируемости отображения.

Так как базисы в пространствах и фиксированы, то представление (8.2) можно записать в координатной форме

, (8.3)

где . Величины являются элементами матрицы линейного оператора из представления (8.2).

Если отображение дифференцируемо в каждой точке , то из формулы (8.3) для матрицы линейного оператора имеем следующее представление:

.

(8.4)

Матрица (8.4) называется матрицей Якоби отображения . Для случая преобразования эта матрица является квадратной и обозначается

,

а её определитель

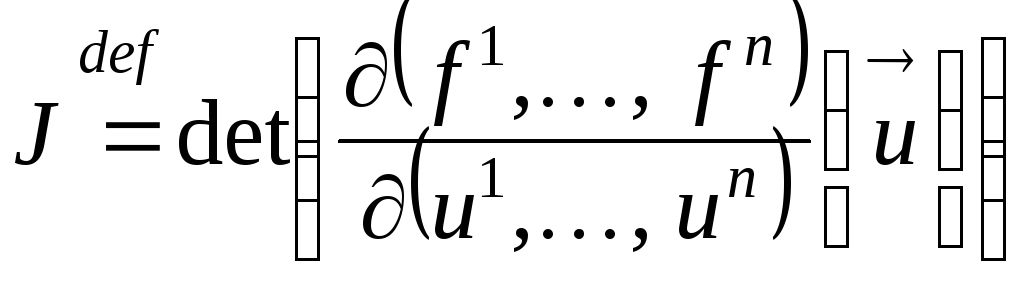
называется якобианом преобразования.

Матрицы Якоби и якобианы называются также функциональными матрицами и функциональными определителями, соответственно.

Общее определение поверхности в евклидовом пространстве , касательная плоскость. Рассмотрим два экземпляра пространств и с базисами и соответственно. Векторы и в этих пространствах представляются в виде разложений

,

.

Определение 8.1. Пусть – некоторая область и – непрерывно дифференцируемое отображение. Множество значений отображения называется (2-мерной) элементарной поверхностью в пространстве .

Поверхность названа элементарной в том смысле, что она является множеством значений одного непрерывно дифференцируемого отображения. Смысл этого замечания состоит в том, что существуют поверхности, которые не могут быть определены при помощи одного отображения.

Из (8.1) видно, что векторное параметрическое уравнение поверхности имеет вид

, (8.5)

и эквивалентно скалярным параметрическим уравнениям

(8.6)

Вектор называется параметрическим вектором, а его координаты – криволинейными или гауссовскими координатами на поверхности , вектор называется текущим или ведущим вектором поверхности. Дальше будем предполагать, что компоненты отображения дифференцируемы по переменным нужное число раз.

Если зафиксирована какая-либо гауссовская координата в области , уравнения (8.5) или (8.6) задают параметризованный путь, лежащий на поверхности . Пусть изменяется , а , тогда вместо (8.5) или (8.6) имеем

, (8.7)

(8.7)

Пусть меняется , а , тогда

, (8.8)

(8.8)

Так как компоненты отображения дифференцируемы по гауссовским координатам нужное число раз, пути с уравнениями (8.7) или (8.8) являются гладкими. Эти пути называются гауссовскими координатными линиями на поверхности . Если ранг матрицы Якоби равен 2, то совокупность системы касательных векторов

(8.9)

путей, проходящих через точку и самой точки поверхности, соответствующей параметрическому вектору , является репером некоторого двумерного линейного многообразия.

Определение 8.2. Линейная оболочка векторов репера называется касательной плоскостью поверхности в точке .

Задавая касательные векторы (8.9) к соответствующим координатным линиям поверхности в каждой точке поверхности в виде , , запишем параметрические уравнения касательной плоскости в виде

После исключения параметров и легко можем получить неявное уравнение касательной плоскости.

Первая квадратичная форма поверхности. Найдём касательный вектор произвольного пути, проходящего по поверхности через фиксированную точку . Путь зададим при помощи нового параметра для параметрического вектора , положив , или , , где . Тогда вместо (8.5) имеем:

. (8.10)

Касательный вектор находим при помощи правила дифференцирования сложной функции:

.

Используя обозначения (8.9), получаем:

. (8.11)

Это соотношение представляет собой разложение касательного вектора любого пути, лежащего на поверхности и проходящего через произвольную точку поверхности, по направляющим векторам касательной плоскости – касательным векторам к гауссовским координатным линиям, проходящим через данную точку поверхности.

Длина дуги пути выражается формулой

. (8.12)

Из формулы (8.12) следует, что дифференциал длины дуги пути может быть вычислен по формуле:

.

С учётом формул (8.9) и (8.11) для произвольного пути на поверхности получаем:

.

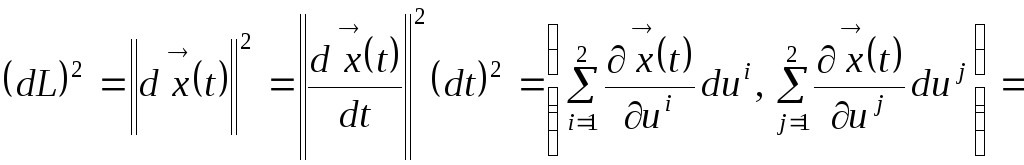
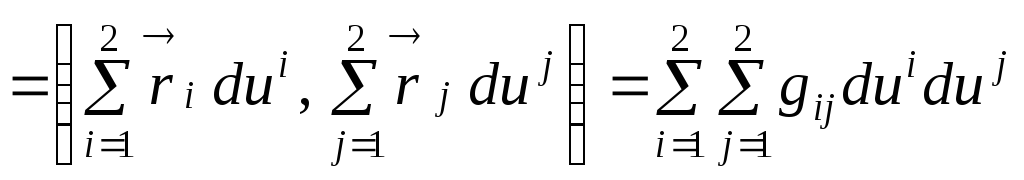Здесь введены обозначения

(8.13)

для метрических коэффициентов на поверхности.

Определение 8.3. Пусть – некоторая поверхность, порождённая непрерывно дифференцируемым отображением . Квадратичная форма

(8.14)

называется первой квадратичной формой, или римановой метрикой на поверхности .

Если известны функции , то подстановка в формулу (8.12) приводит к следующему результату для длины пути на поверхности:

. (8.15)

Для двух пересекающихся в точке поверхности путей с помощью первой квадратичной формы, если известны функции , можно вычислить косинус угла между касательными векторами путей по формуле

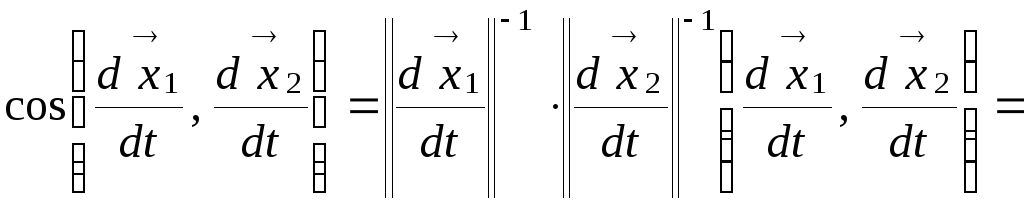
. (8.16)

Первая квадратичная форма (8.14) по построению является положительно определённой, так как определитель её матрицы – это определитель Грама для линейно независимой системы векторов.

Для произвольных векторов в касательной плоскости имеем следующую цепочку:

.

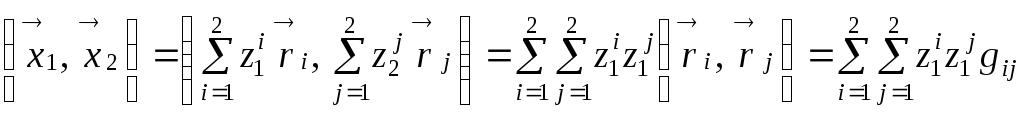Полагая по определению , видим, что скалярное произведение на поверхности по форме совпадает со скалярным произведением в обычном трёхмерном пространстве. Получили следующий результат.