5. РАЗДАТОЧНЫЙ МАТЕРИАЛ по II семестру / Математический анализ. Часть 2 / 1. Лекции / ЛЕКЦИЯ 4. Пути и поверхности в пространстве R3

27

ЛЕКЦИЯ 4.

Движения и пути в пространстве

Вектор-функции и пути. Обозначим, как обычно, через – репер в евклидовом пространстве , тогда каждый вектор запишется в виде следующего разложения .

Пусть – некоторый промежуток числовой оси. На промежутке определим произвольно три действительные функции: . Тогда каждой точке промежутка будет поставлена в соответствие некоторая точка , имеющая радиус-вектор . Отображение промежутка в евклидово пространство называется вектор-функцией из в , определённой на промежутке . Функции называются компонентами, или координатными функциями, вектор-функции .

Определение 4.1. Вектор-функция называется непрерывной ( раз дифференцируемой; раз непрерывно дифференцируемой), если непрерывны ( раз дифференцируемы; раз непрерывно дифференцируемы) её компоненты .

Пример 4.1. Зафиксируем декартову прямоугольную систему координат в пространстве (рисунок 4.1).

Пусть в пространстве движется материальная точка , положение которой в каждый момент времени задаётся радиус-вектором . Если известен закон движения точки – заданы функции , , , где астрономическое время, то для радиус-вектора имеем

.

Получаем отображение промежутка времени в пространство . Разным значениям моментов времени соответствуют разные радиус-векторы, определяющие положение точки в трёхмерном пространстве. Если координатные функции непрерывны, то конец радиус-вектора описывает в пространстве некоторую непрерывную кривую, которая называется годографом или траекторией.

Определение 4.2. Непрерывное отображение любого промежутка действительной числовой оси в евклидово пространство называется движением. Образ промежутка в пространстве называется следом движения или путём.

Конструкцию движения, полгая , можно задать векторным соотношением

, (1)

или эквивалентной системой скалярных соотношений

(2)

Соотношения (1) и (2) называются, соответственно, векторной и скалярной параметризацией движения , а путь , при наличии соотношений вида (1) или (2), позволяющих вычислять координаты точек пути для различных значений параметра , называется параметризованным путём. Если – замкнутый промежуток, то путь называется замкнутым, а точки

, (3)

– началом и концом замкнутого пути , соответственно. Если имеется два пути и , причём конец первого пути совпадает с началом второго пути, то говорят о сумме путей , которая таким образом, с теоретико-множественнй точки зрения является их объединением.

Итак, движение есть непрерывная вектор-функция, определённая на замкнутом или открытом промежутке действительной числовой оси .

Отметим, что вместо термина параметризованный путь для обозначения следа движения часто используют термин парамтризованная кривая, имея в виду возможность изображения множества на чертеже. Формулы примера 4.1 определяют движение ; геометрическое место конечных точек радиус-вектора при различных значениях параметра , является параметризованным путём; точки и – начало и конец пути, соответственно. В пространстве состояний классической механики след движения (путь) – это годограф конечной точки радиус-вектора или траектория материальной точки.

На движения очевидным образом переносятся правила дифференцирования обычных скалярных функций. Если и – два движения, , – соответствующие им параметризации, а – некоторая скалярная функция, то справедливы проверяемые непосредственно формулы дифференцирования:

, (4)

, (5)

. (6)

Примеры параметризованных путей в пространствах и . Приведём некоторые примеры параметризованных путей в двумерном и трёхмерном евклидовых пространствах.

Пример 4.2. Рассмотрим в пространстве движение с параметризацией

, , (7)

где – параметр, принимающий значения в промежутке . Точка исключается, чтобы не повторять точку (для удобства иногда полагают ). Уравнения (7) в векторном виде записываются так:

. (7, а)

Рис. 4.2.

Здесь и – орты локального репера с центром в точке . На рисунке 4.2 в декартовой системе координат изображен след движения – параметризованный путь (7) (орты локальной системы координат не изображены), являющийся окружностью с центром в точке . Действительно, преобразуем параметрические уравнения (7) к виду

, ,

возведём обе их части в квадрат и сложим. В результате получим неявное уравнение параметризованного пути (7)

, (8)

известное ещё из школьного курса математики как уравнение окружности с центром в точке .

Итак, в пространстве движение с параметризацией

, (9)

имеет в качестве своего следа параметризованный путь – окружность (8) радиуса с центром в точке .

Из проведённого рассмотрения следует, что параметр имеет смысл угла между положительным направлением оси и радиус-вектором текущей точки в локальной декартовой системе координат.

Пример 4.3. Обозначим в (7) и рассмотрим параметризованный путь, который получается из пути (7) или, что тоже самое, из (9), сжатием в раз относительно оси , то есть, умножением координаты на величину . Умножая второе уравнение из (7) на , получим:

, .

Обозначая и , имеем:

, . (10)

В уравнениях (10) мы опустили штрихи у индекса координаты . Для случая, когда и , путь с параметризацией

, (11)

Рис. 4.3.

изображён на рисунке 4.3. Отметим, что в этом случае параметр уже не является углом между радиус-вектором текущей точки и осью . Действительно, предположим, что – это угол между осью и радиус-вектором текущей точки . Тогда имеем

,

что конечно при невозможно.

Как известно, путь (11) называется эллипсом. Этот объект изучался в разделе кривые второго порядка в аналитической геометрии.

Для получения неявных уравнений пути (11) нужно исключить из (10) параметр . Для этого умножим первое из уравнений (10) на , а второе на , возведём в квадрат и результаты сложим. После несложных преобразований получим:

. (12)

Для случая и имеем известное из курса алгебры и аналитической геометрии каноническое уравнение эллипса

. (13)

Напомним, что величины и называются, соответственно, большой и малой полуосями эллипса.

Пример 4.4. Рассмотрим в пространстве путь, заданный векторной параметризацией

, (14)

или скалярной параметризацией

. (15)

Исключая параметр из уравнений (15), получаем неявное уравнение пути, которое известно курса аналитической геометрии как уравнение параболы с вершиной в точке (рисунок 4.4, где изображёна часть следа пути на промежутке изменения параметра )

. (16)

Обозначая , и полагая , получаем каноническое уравнение параболы с вершиной в начале системы координат .

Итак, путь, соответствующий движению с параметризацией (15) – это парабола с вершиной в точке .

Пример 4.5. Рассмотрим в пространстве движение , параметризованное векторным соотношением

(17)

или скалярными соотношениями

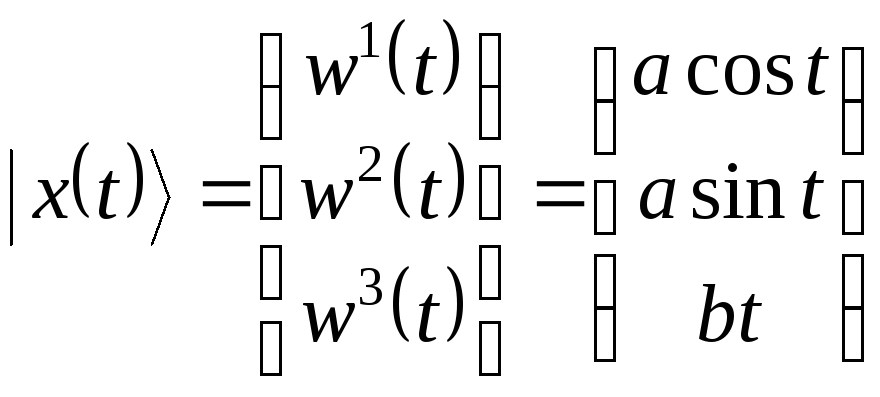. (18)

Путь (18) в пространстве называется винтовой линией. Точки винтовой линии, соответствующие двум значениям параметра и , отличаются друг от друга только своей координатой и при этом, на число . Число называется шагом винтовой линии, а число называется радиусом винтовой линии.

Преобразование параметра. Векторная параметризация

,

где , пути движения задаётся координатными функциями . Продемонстрируем примером, что для одного и того же пути можно ввести, по крайней мере, две различные параметризации.

Пример 1.6. Рассмотрим множество

,

имеющее геометрическим образом верхнюю единичную полуокружность. Пусть . Зададим движение формулами

.

Тогда, очевидно, , , . Поэтому – параметризованный путь. Ранее мы рассмотрели другую параметризацию пути , которая при имеет вид

,

где – угол.

Определение 1.3. Пусть и – два одновременно замкнутых или одновременно открытых промежутка действительной числовой оси . Функция , отображающая промежуток на промежуток , называется преобразованием параметра (от к ), если она непрерывна и биективна.

Таким образом, движения можно параметризовать разными параметрами. Пусть, например, . Тогда по определению, имеем: , . Пусть, далее, и – два преобразования параметра от к и от к , соответственно. Тогда композиция функций является преобразованием параметра от к .

Справедлива следующая лемма.

Лемма 1.1. Пусть – некоторое движение, а

– параметризация пути . Тогда, если – преобразование параметра, то отображение также является движением.

Определение 1.4. Параметризованные движения и называются сильно эквивалентными, если существует преобразование параметра (или преобразование параметра ) такое, что (или, соответственно, ) . Эти движения называются эквивалентными, если существуют такие параметризованные движения , , , , , что , , а параметризованные движения и при сильно эквивалентны.