1. Лекция 1.1. Пространство R3 (1 с.) +

1

ЛЕКЦИЯ 1.1

Трёхмерное евклидово пространство

Понятие вектора. Считаем, что имеется интуитивное понимание размерности обычного пространства. Примером двумерного пространства – плоскости,

странства (или плоскости) будем понимать такую пару точек, для которой указано, какая точка является первой, а какая второй.

двигать один из них вдоль этого отрезка с сохранением его направления до совпадения начальных точек обоих векторов, будем говорить о параллельном переносе этого вектора. Два вектора считаются равными, если они могут быть полностью совмещены как направленные отрезки путём параллельного переноса.

ленного отрезка AB . Величина вектора по определению равна его длине, взятой со знаком «плюс», если его направление совпадает с выбранным направлением оси, на которую он помещён, и со знаком «минус» – в противном случае.

Для векторов определяются две операции – умножение вектора на число

При умножении вектора на некоторое число R его длина умножается на абсолютную величину этого числа, направление при 0 не изменяется,

а при 0 изменяется на противоположное. На рисунке 1. б вектор AC есть

2

результат умножения вектора AB на некоторое число 0, что записывается

Отметим, что операция сложения векторов является алгебраической, так как она каждым двум векторам трёхмерного пространства (плоскости) ставит в соответствие третий вектор того же пространства (плоскости). Кроме этого, операция сложения векторов коммутативна

(рисунок 1. в), и имеет обратную операцию, которая называется вычитанием

ра на число является внешней бинарной операцией, так как определена для пары, один элемент которой принадлежит множеству векторов пространства

Декартова система координат. Координаты точек и векторов. Ортого-

нальной декартовой системой координат в пространстве (на плоскости) назы-

вается совокупность трёх (двух) пересекающихся, взаимно перпендикулярных осей и точки их пересечения – начала координат. Напомним известное из средней школы построение декартовой системы координат для случая плоскости.

Проводим на плоскости две взаимно перпендикулярные прямые и обозначаем точку их пересечения буквой O (рисунок 1.2). На горизонтальной и верти-

3

кальной прямых откладываем отрезки OE1 и OE2 одной и той же длины. Упорядочим тройку точек O; E1; E2 так, чтобы кратчайший поворот отрезка OE1 до совмещения с отрезком OE2 осуществлялся против часовой стрелки – это направление принимаем за положительное.

Прямую, проходящую через точки O и E1 , назовём осью OX 1 , а прямую,

проходящую через точки O и E2 назовём осью OX 2 . На каждой оси поместим действительные числа, отмечая их положение пропорционально величине соот-

взаимно однозначное соответствие точка плоскости, в проекции которой на оси OX k находится число xk k 1, 2 . Таким образом, между точками плоскости и парами действительных чисел – их координатами x1 на оси OX 1 и x2 на оси OX 2 , установлено биективное соответствие, то есть плоскость является прямым произведением R R R2 . По этой причине плоскость называется про-

странством R2 (читается “пространством эр два”). Поясним, что речь идёт о модели плоскости, но слово модель обычно опускают.

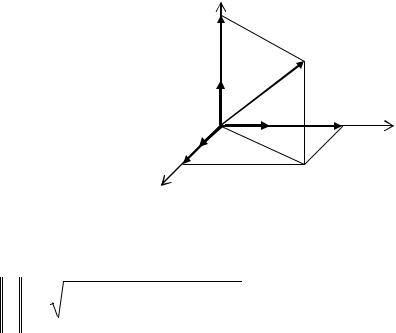
Если ортогональная декартова система координат введена в трёхмерном пространстве, то точке P ставятся в соответствие три действительных числа –

декартовы координаты, которые по определению равны величинам коорди-

натных проекций OA, OB и OC радиус-вектора OP точки P , началом ко-

торого является начало системы координат, а концом – точка P . На рисунке 1.3

величины x1, x2 , x3 – это координаты точки P и её радиус-вектора OP . Нача-

лу системы координат O ставится в соответствие нуль-вектор – направленный отрезок с совпадающими начальной и конечной точками и, следовательно,

имеющий нулевую длину. Для нуль-вектора направление не определено.

Применяя теорему Пифагора, нетрудно показать, что длина или норма ра-

диус-вектора x в трёхмерном пространстве вычисляется по формуле

В случае плоскости в формуле отсутствует третья координата.

Нетрудно видеть, что обычное трёхмерное пространство является произве-

дением R R R R3 . Как и в случае плоскости, речь идёт, вообще говоря, о

модели трёхмерного пространства.

Представление радиус-вектора в виде разложения по базисным векто-

рам. Рассмотрим случай радиус-векторов, причём для простоты и наглядности ограничимся случаем векторов на плоскости. Сначала рассмотрим представление радиус-вектора через его координаты.

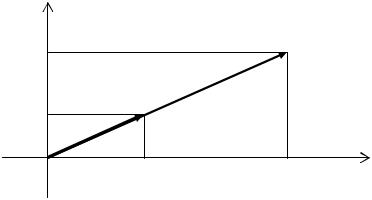
На рисунке 1.4 представлен радиус-вектор x в декартовой системе коорди-

направленные в положительных направлениях осей и имеющие единичную дли-

7

Аналогичные (1.7) равенства справедливы, конечно, и в случае трёхмерного про-

Итак, если векторы равны, то и их координаты относительно декартовой системы координат также равны.

Справедливо очевидно и обратное, а именно: если координаты двух век-

торов относительно некоторой фиксированной системы координат равны,

то они равны в том смысле, что их можно полностью совместить как направленные отрезки путём параллельного переноса.

Рассмотрим теперь операцию сложения радиус-векторов по правилу параллелограмма для случая плоскости, которая представлена на рисунке 1.5. Вводя

обозначения для координат векторов x , y и z , записывая для векторов разло-

y по правилу параллелограмма, получаем:

Учитывая равенства (1.7), получаем

Таким образом, при сложении радиус-векторов их координаты относительно канонического базиса складываются.

8

Конечно, аналогичный результат для суммы векторов справедлив с учётом (1.3), (1.7’) и в пространстве R3 :

Таким образом, при сложении векторов их соответствующие коорди-

наты относительно канонического базиса декартовой системы координат складываются.

Рассмотрим умножение вектора на число (рисунок 1.6), начиная снова для простоты со случая пространства R2 . Рассмотрим только координату вектора по оси OX 1 . Из подобия треугольников OCD и OAB , а также из того, что длины

Аналогичное равенство имеет место и в случае пространства R3 :

9

Итак, при умножении вектора на число все его координаты относи-

тельно канонического базиса декартовой системы координат умножаются на это число.

ваем сразу пространство R3 ). Умножая каждый из векторов на соответствующий множитель 1, 2 , 3 , складывая получившиеся векторы и приравнивая результат к нулевому вектору, получаем:

Векторная величина в левой части (1.13) называется линейной комбинацией

(1.14’) означают, что линейная комбинация векторов канонического базиса имеет своим значением нулевой вектор только при их выполнении. Это свойство относится ко всей системе векторов канонического базиса и называется линейной независимостью системы. Свойство системы векторов быть линейно независимой выполняется не только для векторов канонического базиса, но и для бесконечного числа систем трёх некомпланарных (в случае плоскости – для бесконечного числа систем неколлинеарных) векторов.