
- •Введение
- •Раздел «Электростатика»
- •Вопросы по программе дисциплины «Физика», раздел «электростатика»
- •Памятка студенту
- •Желаем творческих успехов в вашей нелегкой самостоятельной учебной деятельности!!!
- •1. Взаимодействие неподвижных зарядов
- •1.1. Закон Кулона
- •1.2. Расчет равнодействующей силы системы неподвижных точечных зарядов
- •1.3. Равновесие зарядов при действии нескольких сил
- •1.4. Взаимодействие зарядов, равномерно распределённых на линии, на поверхности и в объёме
- •2. Характеристики электростатического поля
- •2.1. Напряжённость электростатического поля
- •2.2. Поток вектора напряженности. Теорема Остроградского – Гаусса
- •2.2.1. Расчет напряженности поля, образованного точечными зарядами
- •2.2.2. Расчет напряженности поля, созданного заряженными: бесконечно длинным цилиндром (нитью), бесконечной плоскостью, сферой, шаром
- •Примеры расчёта некоторых полей
- •2.2.3. Расчет напряженности поля, созданного заряженным телом простой формы
- •2.3. Потенциал. Эквипотенциальные поверхности
- •Свойства эквипотенциальных поверхностей:
- •3. Связь между напряжённостью электростатического поля и потенциалом
- •4. Работа поля по перемещению заряда. Потенциальная энергия
- •5. Электрическая ёмкость. Конденсаторы
- •Параллельное соединение конденсаторов
- •Последовательное соединение конденсаторов
- •Задачи для самостоятельного решения
- •Ответы к заданиям для самостоятельной работы к разделу 1.1
- •К разделу 1.2
- •К разделу 2.1
- •К разделу 2.3
- •К главе 5
- •Список рекомендуемой литературы Основной
- •Дополнительный
- •Оглавление
1.3. Равновесие зарядов при действии нескольких сил
Если по условию задачи заряд находится в равновесии, это значит, что векторная сумма сил, действующих на заряд, равна нулю. В зависимости от условия задачи, это могут быть силы Кулона, сила тяжести, сила Архимеда и т. д.
Рекомендуемая последовательность решения задач:
сделать рисунок, на котором указать расположение всех зарядов;
построить векторную сумму всех сил, действующих на заряд;
записать I закон Ньютона в векторном виде:
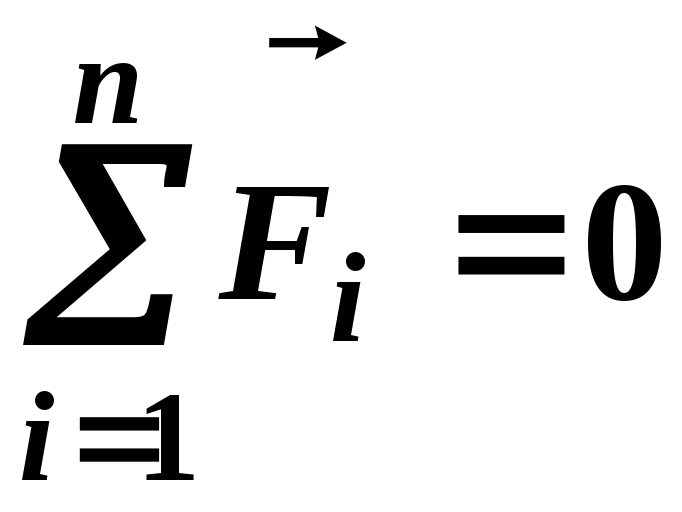 ;
;выбрать направление осей координат и разложить все силы на составляющие;
записать I закон Ньютона в проекциях на каждую ось;
выразить искомую величину.

Задача 1.3. Расстояние между двумя разноимёнными точечными зарядами q1 = +q и q2 = – 2q равно r. На каком расстоянии от первого заряда r1 на линии, соединяющей эти заряды, нужно поместить третий заряд Q, чтобы он находился в равновесии?
Решение. Сделаем рисунок и проанализируем задачу.
Заряд Q может располагаться в одной из трёх областей (рис. 5 а): I – слева от заряда q1; II – между зарядами q1 и q2; III – справа от заряда q2.
П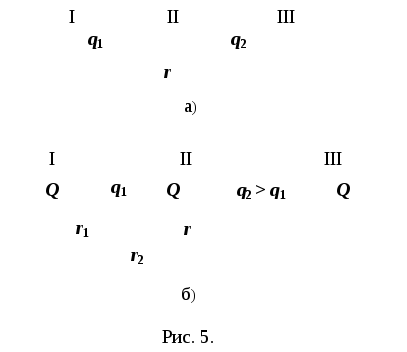 устьQ
> 0.
устьQ
> 0.
Поместим заряд Q поочерёдно в каждую из этих областей, расставим силы, действующие на этот заряд, и методом исключения отбросим области, где не выполняется I закон Ньютона (рис. 5, б).
На
заряд Q
со стороны зарядов q1
и q2
действуют силы с соответствующими
индексами
![]() .
.
Запишем I закон Ньютона в векторном виде:
![]() .
.
Чтобы
он выполнялся, векторы сил
![]() должны бытьодинаковы
по модулю и противоположны по направлению.
должны бытьодинаковы
по модулю и противоположны по направлению.
Из рисунка видно, что в области II силы направлены в одну сторону, поэтому здесь равновесие невозможно.
В областях I и III силы направлены в разные стороны, т. е. равновесие теоретически возможно.
Теперь
проанализируем модули векторов
![]() .
Из закона Кулона (1.2) следует, что модуль
силы зависит от величины заряда и от
расстояния до него. Любая точка в областиIII
находится ближе к бόльшему заряду
q2,
следовательно, сила
.
Из закона Кулона (1.2) следует, что модуль
силы зависит от величины заряда и от
расстояния до него. Любая точка в областиIII
находится ближе к бόльшему заряду
q2,
следовательно, сила
![]() в этой области всегда будет больше, чем
в этой области всегда будет больше, чем![]() ,
поэтому в этой области равновесие тоже
невозможно.
,
поэтому в этой области равновесие тоже
невозможно.
Остаётся область I. Для неё запишем в скалярном виде:
![]() .
.
По закону Кулона:
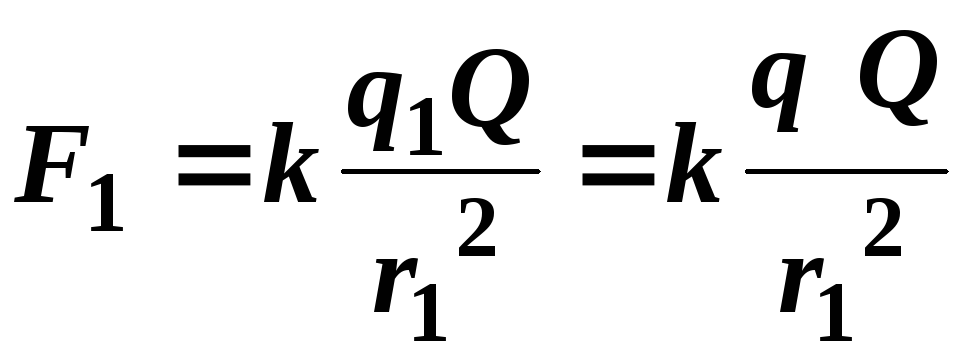 ;
; 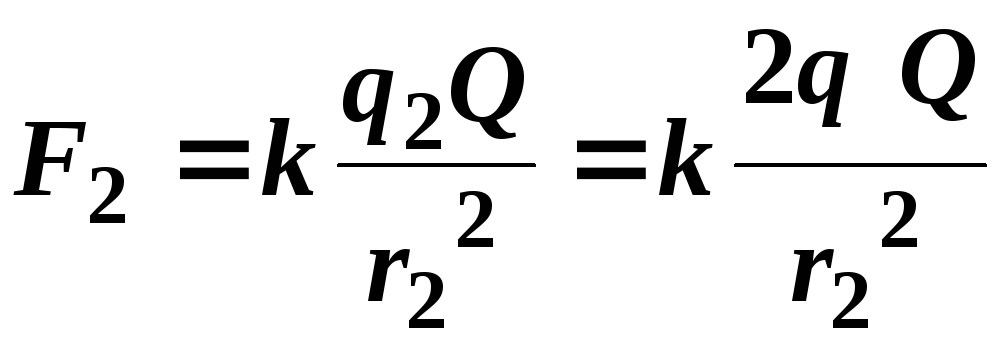 .
.
Приравнивая
правые части с учётом того, что
![]() ,
получим:
,
получим:
![]() или
или
![]() .
.
Произведём необходимые математические преобразования:
![]()
![]() .
.
Окончательно получим:
![]() .
.
Если
заряд Q
будет отрицательный, то поменяются
направления сил
![]() ,
но результат от этого не изменится.
,
но результат от этого не изменится.
Задача 1.4. Два одинаковых шарика подвешены на нитях одинаковой длины, закреплённых в одной точке. После сообщения шарикам заряда +q0 они оттолкнулись и разошлись на угол 2α. Найти массу каждого шарика и силу натяжения нити, если расстояние от центра шарика до точки подвеса равно ℓ.
Р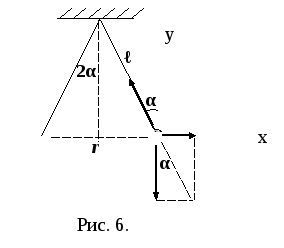 ешение.
Так как шарики одинаковы и находятся в
одинаковых условиях, то достаточно
рассмотреть силы, действующие на один
из шариков (рис. 6). На каждый шарик
действует сила тяжести
ешение.
Так как шарики одинаковы и находятся в
одинаковых условиях, то достаточно
рассмотреть силы, действующие на один
из шариков (рис. 6). На каждый шарик
действует сила тяжести
![]() ,
сила натяжения нити
,
сила натяжения нити
![]() и сила электрического взаимодействия
(отталкивания)
и сила электрического взаимодействия
(отталкивания)![]() .
.
Так как шарики находятся в равновесии, то по первому закону Ньютона:
![]() .
.
Выберем произвольно направления осей ox и oy и найдём проекции всех сил на эти направления. Запишем I закон Ньютона в проекциях на выбранные направления:
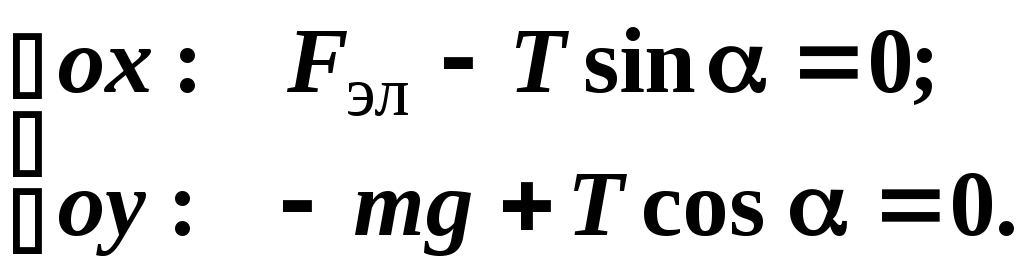
Получили систему из двух уравнений с двумя неизвестными. Решая эту систему, найдём искомые величины.
Из первого уравнения выразим силу натяжения нити:
![]() .
.
По закону Кулона
![]() ,
,
где
![]() – заряд каждого шарика. Так как шарики
одинаковы, то заряды тоже одинаковы (по
закону сохранения заряда).
– заряд каждого шарика. Так как шарики
одинаковы, то заряды тоже одинаковы (по
закону сохранения заряда).
Из рисунка выразим расстояние между шариками:
![]() .
.
Окончательно получим:
![]() .
.
Чтобы найти массу, преобразуем систему к следующему виду:
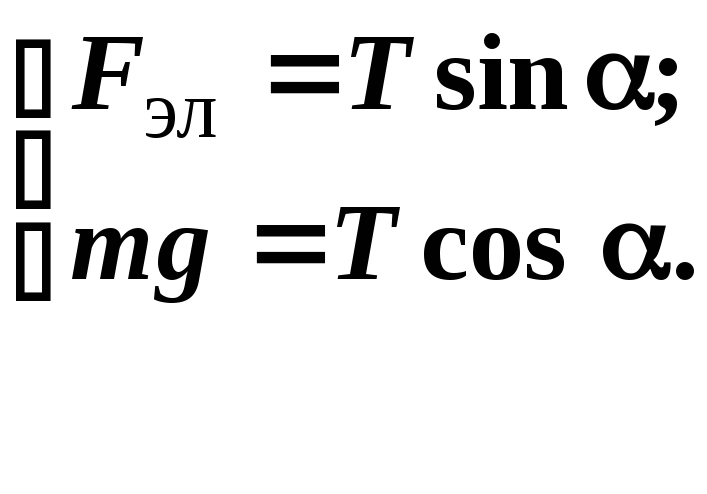
Поделив почленно первое уравнение на второе, получим:
![]() .
.
Задача 1.5. Положительно заряженный шар плотностью ρш и радиусом R помещён в жидкость плотностью ρж. Найти заряд шара, если в однородном электростатическом поле напряжённостью Е, направленном вертикально вверх, он оказался взвешенным в жидкости.
Р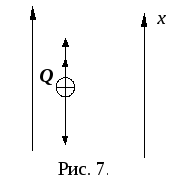 ешение.На шар
действуют три силы: сила тяжести
ешение.На шар
действуют три силы: сила тяжести
![]() ,
направленная вниз, выталкивающая сила
Архимеда
,
направленная вниз, выталкивающая сила
Архимеда
![]() ,
направленная вверх, и электростатическая
сила
,
направленная вверх, и электростатическая
сила![]() ,
которая совпадает с направлением
напряжённости
,
которая совпадает с направлением
напряжённости![]() (рис. 7). Так как шар находится в состоянии
равновесия, то для него выполняетсяI
закон Ньютона:
(рис. 7). Так как шар находится в состоянии
равновесия, то для него выполняетсяI
закон Ньютона:
![]() .
.
Выберем произвольно направление оси х, на которую будем проецировать силы.
Запишем I закон Ньютона в проекциях на выбранное направление:
Fарх + Fэл – mg =0.
Подставим в эту формулу выражения для сил:
![]() ;
;
![]() .
.
Выразим массу шара через его плотность и объём:
![]() .
.
После математических преобразований получим:
![]() .
.
Предлагаем проанализировать случаи, когда поле направлено вертикально вниз.
