3. Интеграл Шварца-Кристофеля

Если функция реализует конформное отображение верхней полуплоскости Imz>0 на внутренность многоугольника при вершинах, причем известны точкидействительной оси, соответствующие вершинам этого многоугольника, то f(z) представляется интегралом

^(₁^-1)(-a₂)^(₂^-1)…(-a_n-1) ^(_n-1^-1)d+C₁

C, C1, Z0- некоторые константы

Обычно известны Ак, , а ак- неизвестны

4. Определение величин углов между соседними отрезками

Примечание1.Выбором трех констант С,С₁, z₀ можно произвольно задать три точки иза_к

Примечание 2.Одна или несколько вершин многоугольника лежат в бесконечно удаленной точке.

Формула Шварца-Кристофеля остается в силе и для многоугольников,у которых одна или несколько вершин лежат в бесконечно-удаленной точке, если при этом угол между двумя прямыми с вершиной в бесконечности определяется как угол в конечной точке их пересечения, взятый с обратным знаком.

Примечание3.Одна из вершин многоугольника – образ бесконечно удаленной точки.

Если одной из вершин многоугольника соответствует бесконечно удаленная точка, то относящийся к этой вершине множитель в формуле Шварца-Кристофеля выпадает

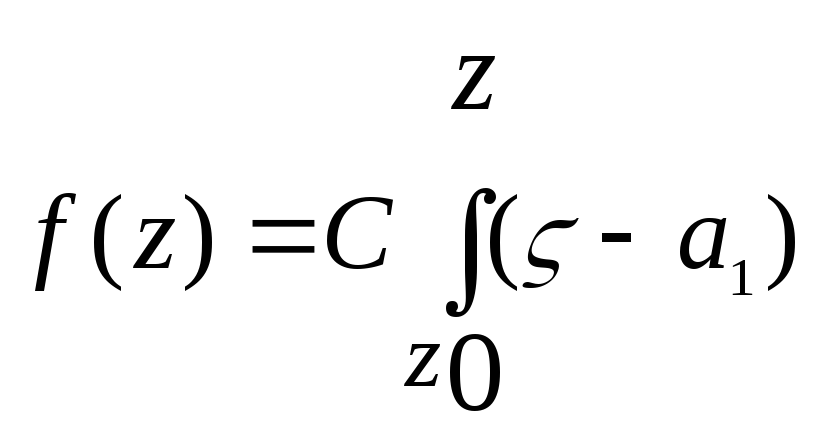(1-1)(-a2)(2-1)…(-an-1) (n-1-1)d+C1

(1-1)….(an-a1-)(n-1-1)(n-1)=

=A(1-1)….(-an-1)(n-1-1)

(1-1)(an-a2)(2-1)…(an-an-1) (n-1-1)(-1) (n-1)

5. Пример1.

Найти функцию конформно отображающую верхнюю полуплоскость Imz>0 на сектор 0<argw<

Если потребовать

6. Пример2.(из тфкп)

Пусть D-полуплоскость Imz>0 с разрезом по отрезку [0, ih],h>0. Найдем конформное отображение области D на верхнюю полуплоскость Imw>0

a)



б)

0

в

w

)

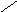
Функция конформно отображает область D на полуплоскость Imw>0

Справка

^z2

^x2=-1e^x2

A₂

;

^x2

A₃

1.

a₁=0 a₃=-1 a₂=

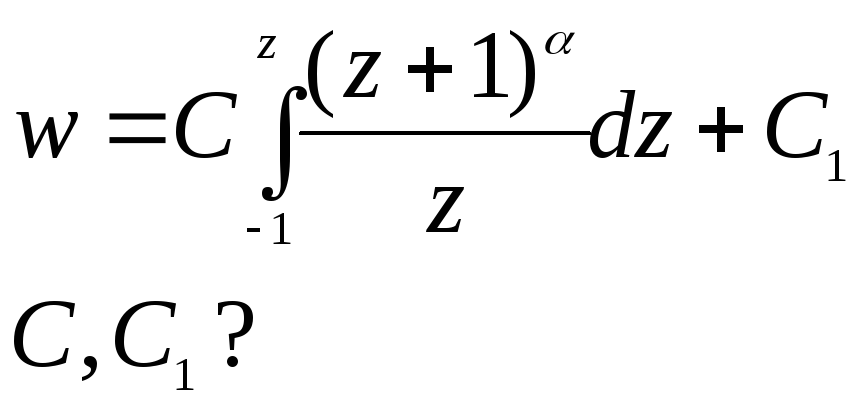
z=1C₁=ih

C-?

dz=i

;

;

A₁

;

z

; где

7. Две прямолинейные вихревые нити. Движение системы вихрей.

Исследуем перемещение вихрей в жидкости.

Для скорости 1-го вихря

Для скорости 2-го вихря

или

- «интегралы движения центра инерции» системы двух вихрей

- координаты «центра инерции»

(1)-(3) (2)-(4)

или r=const

Частный случайцентр инерции в,т.к.

вихри перемещаютсяOy

Система вихрей:

;

; (*)

«» означает пропуск члена, соответствующегоk=l

(*)Г_l

и просуммируем по l от 1 до n

;

;

Если , то

(*)Г_l и суммируя по l от 1 до n

(*)Г_l и суммируя по l

r_kl- расстояние между вихрями z_k и z_l

2. Сжимаемая жидкость

   1. Линеаризованное уравнение распространения звука

; ;<<

мало ,

(2.1)

(2.2)

(2.3.)

(2.4.)

(2.3.)-

Задача.В идеальной сжимаемой жидкости или газе в отсутствие массовых сил при механическом равновесии, когда всюду, давление и плотность заданы величинами=const,

. В результате малого возмущения возникло движение, в котором

, причем , а также их производные малы. Движение баротропно. Написать линеаризованную систему уравнений для функций . Показать что они удовлетворяют волновому уравнению.

Вектор скорости любого движения может быть представлен суммой потенциального и соленоидального векторов

Написать уравнения для и

Решение.

Замкнутая система уравнений для баротропного движения идеальной жидкости или газа:

При система удовлетворена, еслиp=p(). В результате линеаризации получаем

Задача. Найти общее решение линеаризованной системы уравнений для малых возмущений в виде плоских волн:

Общее решение волнового уравнения

Подставив это решение в систему уравнений, получим для других функций равенства:

, где С=const

Задача

Плоская звуковая волна, распространяющаяся вдоль оси х, падает на границу раздела плоскость x=0. Давление в падающей волне. Найти амплитуды давленияв отраженной ив прошедших волнах, при заданных значениях плотностейи скоростейв равновесном состоянии.

- коэффициент отражения

- коэффициент преломления

Оценить величины амплитуд отраженной и прошедшей волн

а) из воздуха в воду

б) из воды в воздух

скорость звука в воде 1400 м/с

Решение

В области (1)- две волны: падающая и отраженная

В области (2)- только прошедшая волна

Для скоростей частиц соответственно:

На границе x=0 должны выполняться условия на контактном разрыве

; , где

=;=

1. из воздуха в воду ;, следовательно

2. из воды в воздух , т.е. звуковые возмущения из воды в область, занятую воздухом почти не проходят.

Задача Плоская монохроматическая звуковая волна вдоль осиимеющая потенциал, составляя уголс нормалью.

Плотности и скорости звука в обеих средах известны. Найти углы , определяющие направления распространения отраженной и преломленной волн. Показать, что припроходящая волна существует не при любых углах падения

Решение

y

Ось y–по границе раздела, ось х – по нормали к ней

В падающей волне

Волновой вектор имеет вид:

В отраженной и преломленной волнах возмущение представляем в форме

Наличие границы не влияет на вид всех функций от yиt, вновь возбужденные волны имеют туже частоту иyкомпоненту волнового вектора:

,

Для падающей и отраженной волн в среде (1) скорость звука одна и та же

. Следовательно и

Во второй среде;

Если а₂/a₁>>1 – прошедшая волна отсутствует для не слишком малых углов(полное внутреннее отражение.) Это свойство распространения волн вблизи границ слоев с разными акустическими свойствами лежит в основе эффекта волновода – звуковые возмущения не выходят за пределы слоя, в котором скорость звука меньше, чем в окружающих областях, тем самым не рассеивают свою энергию и меньше затухают.