стат / Задача 11

Задача 11. Вычислить теплоемкость трехмерного и двумерного идеального ферми-газа при низкой температуре.

Решение. Рассмотрим сначала трехмерный случай. Энергия ферми-газа (частиц со спином ½) определяется соотношением

(1)

Здесь мы записали число состояний в виде

(2)

Функция распределения Ферми имеет вид

,

где - химический потенциал.

Число частиц определяется соотношением

(3)

При нулевой температуре отсюда имеем

Согласно (2) тогда получим для плотности состояний

. (4)

Получим общее выражение для интегралов такого типа при низких температурах. Замена приводит к выражению

Далее преобразуем последний из интегралов в правой части этого выражения

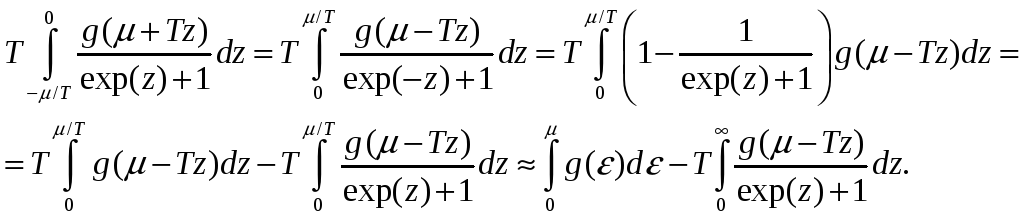
Здесь мы заменили верхний предел во втором интеграле на бесконечность, так как возникающая поправка экспоненциально мала, а мы будем учитывать только степенные поправки по температуре. Итак,

.

Разлагая в ряд Тейлора числитель в интеграле, находим

Так как (интеграл вычисляется с помощью теории вычетов)

,

То окончательно получим общую формулу, справедливую при низких температурах (малых по сравнению с энергией Ферми)

(5)

На основе этой формулы вычисляем энергию, определяемую соотношением (1):

(6)

Аналогично для числа частиц получим

.

Отсюда находим поправку к химическому потенциалу при низких температурах

. (7)

Подставляя (7) в (6), находим поправку к энергии

.

Для теплоемкости получим

. (8)

Здесь энергия Ферми равна

. (9)

Теперь обратимся к двумерному ферми-газу. Число состояний этом случае записывается как

Здесь - площадь системы. При нулевой температуре имеем

При малой температуре, но отличной от нуля, число частиц выражается соотношением

Согласно (5) Поэтому химический потенциал не содержит поправок, квадратичных по температуре, т.е. Энергия системы согласно (5) равна

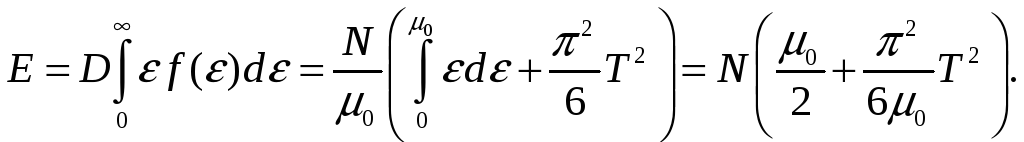
Таким образом, энтропия равна

(10)