стат / Задача 14

Задача 14. Гамильтониан ферромагнетика в модели Изинга в магнитном поле h имеет вид

.

Здесь - спины электронов, индексы i,k нумеруют узлы кристаллической решетки ферромагнетика, - магнетон Бора. Обменное взаимодействие –V обеспечивает параллельные спины при низких температурах (спонтанную намагниченность). В приближении самосогласованного поля определить температуру фазового перехода (температуру Кюри), магнитную восприимчивость выше температуры Кюри и спонтанную намагниченность ниже температуры Кюри.

Решение. Выделим один спин и в соответствии с данной формой гамильтониана введем самосогласованное поле, действующее на этот спин со стороны других спинов, заменяя другие спины средним значением спина :

.

Здесь z – число ближайших соседей к данному спину, которые и учитываются во взаимодействии. Среднее значение намагниченности (магнитный момент единицы объема) определяется как

.

Здесь n – концентрация свободных электронов. Следовательно, самосогласованное поле можно записать в виде

.

С другой стороны, среднее значение величины намагниченности определим с помощью усреднения по классическому распределению Больцмана (при этом мы предполагаем, что температура Т достаточно велика по сравнению с энергией Ферми)

(1)

Здесь .

Если (слабое магнитное поле), то из этого соотношения следует, что

Отсюда находим парамагнитную восприимчивость

(2)

При отсюда получим , что совпадает с классическим выражением для парамагнитной восприимчивости, найденной в задаче 12 (уравнение (15)), как и должно быть. Восприимчивость определена при температуре выше критической температуры (температуры Кюри)

(3)

В этой точке восприимчивость обращается в бесконечность.

Ниже точки Кюри возникает спонтанная намагниченность. Ее величина находится из (1), если положить h = 0. Получаем неявное уравнение

(4)

При Т = 0 отсюда получим . Найдем решение (4) при температурах вблизи температуры Кюри, где намагниченность мала. Разлагая правую часть (4) в ряд Тейлора, получим

Отсюда

(5)

На рис. 1 представлена зависимость безразмерной величины от согласно неявному уравнению (4). Она согласуется с оценками, приведенными выше.

Рис. 1

В заключение рассмотрим случай сильного магнитного поля. Обозначим , и Уравнение (1) для намагниченности перепишем в виде

(6)

Дифференцируя его по x, получим уравнение для обезразмеренной магнитной восприимчивости :

.

Подставляя (6) в это соотношение, находим

Восприимчивость обращается в бесконечность при откуда . Подставляя это соотношение в (6), получим неявное уравнение

(7)

Оно неявно определяет критическую точку Кюри t через напряженность магнитного поля x. Если x = 0, то t = 1 (случай слабого поля, рассмотренного выше). На рис. 2 представлена зависимость обезразмеренной критической температуры от обезразмеренного магнитного поля согласно неявному уравнению (7)

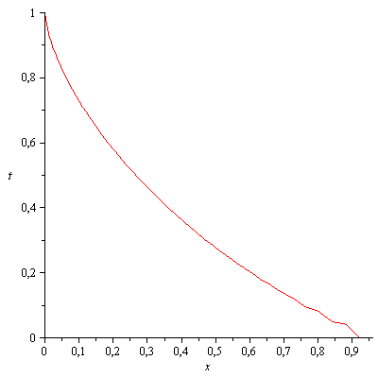
Рис. 2

Из этого рисунка следует, что при критическом поле критическая температура обращается в нуль, т.е. спонтанная намагниченность исчезает.