стат / Задача 2

Задача 2. Найти теплоемкость идеального одноатомного газа, помещенного в гравитационное поле в сосуде высотой h.

Решение. Энергия атома в гравитационном поле имеет вид

(1)

Вычисляем классическую статистическую сумму сначала для одного атома. Координатная часть ее имеет вид

(2)

Здесь - площадь сосуда.

Импульсная часть статистической суммы равна

(3)

Итак,

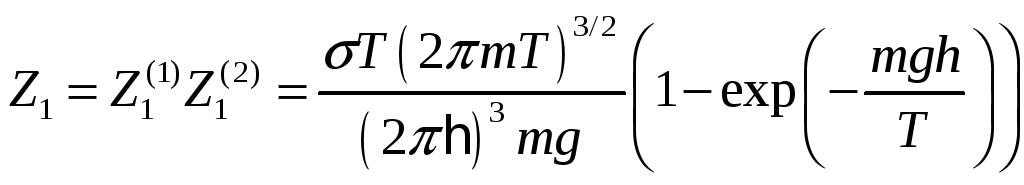. (4)

Статистическая сумма для N частиц равна (используя формулу Стирлинга)

(5)

Выразим свободную энергию через найденную статистическую сумму

. (6)

Далее определим энергию системы Учитывая, что при фиксированном объеме , получим и Подставляя в это соотношение выражение (6) для свободной энергии, находим

(7)

Теплоемкость при постоянном объеме определяется как

. (8)

Если , из (8) следует, что Если, наоборот, , то из (8) следует, что В последнем случае это означает, что гравитационными силами можно пренебречь. При увеличении высоты сосуда теплоемкость растет, так как растет потенциальная энергия атомов.

На рис. 1 представлена зависимость как функция согласно (8). Видно, что выход на значение достигается при достаточно большом значении параметра > 10.

>

Рис. 1.