стат / Задача 13

Задача 13. Найти диамагнитную восприимчивость идеального газа свободных электронов в магнитном поле. Рассмотреть случаи низких и высоких температур.

Решение. Сначала обратимся к случаю классической статистики высоких температур - энергия Ферми. В слабом магнитном поле Н, направленном вдоль оси z, квантовомеханическая энергия электрона равна (без учета спина)

(1)

Здесь - магнетон Бора. Вычислим вырождение каждого из этих дискретных уровней в кубическом ящике с длиной L:

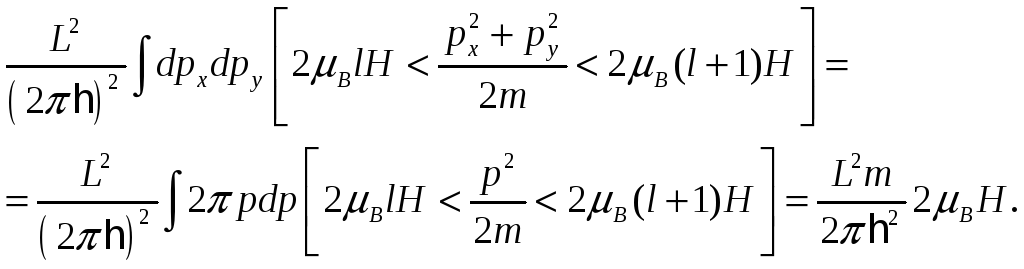
Следовательно, число состояний равно

(2)

(дополнительный фактор 2 появляется из-за двух проекций спина электрона).

Вычисляем классическую статистическую одноэлектронную сумму для одного электрона (бесконечная геометрическая прогрессия)

(3)

Получим

(4)

Для N электронов статистическая сумма равна (используя формулу Стирлинга для N!)

(5)

Свободная энергия определяется как Получаем

Намагниченность (магнитный момент единицы объема) равна

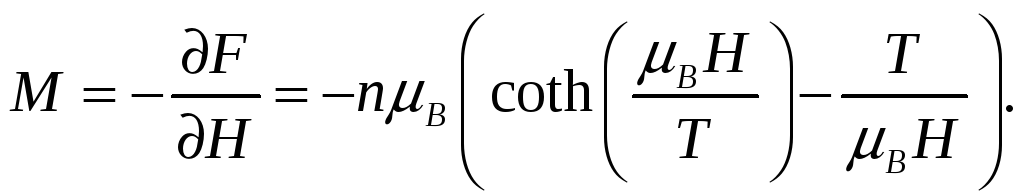(6)

Здесь - концентрация электронов. Магнитная проницаемость равна

(7)

Если , то из (7) получим

. (8)

Она отрицательна (диамагнетизм) и в 3 раза меньше, чем парамагнитная восприимчивость, обусловленная спином электрона (см. задачу 10, формула (15)). Если, наоборот, , то из (7) получим, что восприимчивость очень мала:

На рис. 1 представлена зависимость безразмерной величины от безразмерной величины

Рис. 1

Теперь обратимся к случаю низких температур В этом случае рассмотрим только случай слабых магнитных полей Квантовая статистическая сумма теперь определяется статистикой Ферми, т.е. свободная энергия

после подстановки числа состояний (2) принимает вид

. (9)

Вычисляем сумму в (9) с помощью формулы Эйлера-Маклорена

Здесь обозначено

Следовательно, Таким образом, из (9) получим

Вклад в магнитную восприимчивость дает только последнее слагаемое в (10), квадратичное по магнитному полю, так как Получаем:

.

При низкой температуре функция распределения Ферми представляет собой ступенчатую функцию Хевисайда, так что

Так как энергия Ферми при нулевой температуре , то окончательно получаем

(10)

Мы видим, что как и в случае высоких температур, в случае низких температур диамагнитная восприимчивость в три раза меньше парамагнитной восприимчивости, найденной в задаче 12 (формула (7)).