стат / Задача 16

Задача 16. Используя функционал Гинзбурга-Ландау, оценить радиус корреляций в теории фазовых переходов второго рода.

Решение. При рассмотрении модели Изинга для ферромагнетика в задаче 14 было показано, что при некоторой критической температуре Т_С происходит фазовый переход второго рода. Ниже этой температуры имеется спонтанная намагниченность М (в отсутствие внешнего магнитного поля). В самой критической точке и выше критической температуры спонтанной намагниченности нет. В окрестности критической точки термодинамический потенциал , определенный при постоянном объеме V и температуре Т, можно разложить в ряд по М. Это разложение содержит только четные степени М, так как термодинамический потенциал не может зависеть от знака М (магнитный момент меняется при изменении знака времени, а потенциал – нет). Итак, для потенциала, отнесенного к единице объема, можно написать

(1)

Величина М определяется из минимума потенциала:

(2)

Здесь величина b > 0 берется в критической точке (при b < 0 потенциал не имеет минимума при больших значениях намагниченности). Значение А = 0 в критической точке. Разлагая ее в ряд Тейлора, получим и

Таким образом, выше критической точки спонтанная намагниченность отсутствует.

В неоднородной среде намагниченность зависит от координаты. Для плавных изменений намагниченности в пространстве можно разложить ее в ряд по производным по координате. В соответствии с приведенными выше соображениями о четности потенциала получим в простейшей среде с кубической симметрией обобщение выражения (1), записанное для термодинамического потенциала всей среды

(3)

Здесь мы ограничились членами второго порядка по намагниченности.

Флуктуация потенциала в соответствии с (3) имеет вид

(4)

Она содержит только квадратичные члены по флуктуациям намагниченности, так как линейные члены исчезнут при усреднении по флуктуациям. Разложим флуктуацию намагниченности в ряд Фурье:

.

Подставляя эти разложения в (4), учтем, что только члены вида внесут ненулевой вклад при интегрировании экспонент по объему. Таким образом, получаем

Согласно распределению Гиббса вероятность данной флуктуации имеет вид

. (5)

Распределение (5) позволяет найти среднее значение флуктуации намагниченности

(6)

Флуктуация велика, когда знаменатель в (5) мал, т.е. когда величина вблизи критической точки мала. Это как раз соответствует длинноволновым флуктуациям, что предполагалось выше.

Введем обозначение для корреляционной функции флуктуаций намагниченности

Переходя к представлению Фурье, получим

Заменяя суммирование интегрированием, находим

(7)

Подставляя (6) в (7), находим

(8)

Вычисляя интеграл, находим (выражение (8) математически представляет собой фурье-компоненту экранированного кулоновского потенциала)

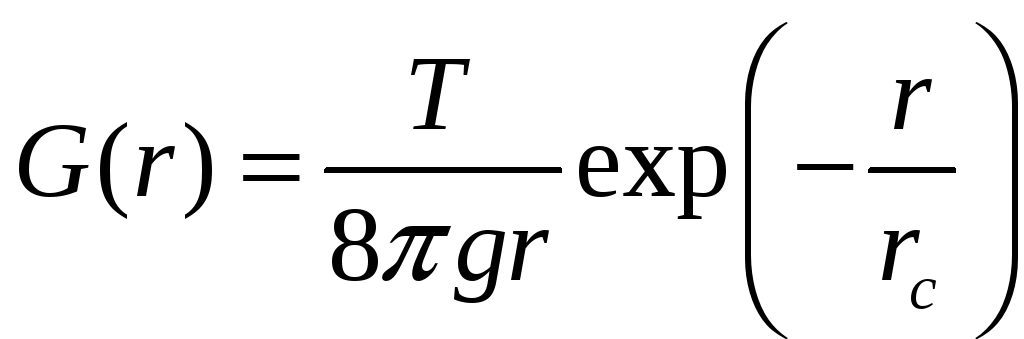(9)

Здесь обозначено

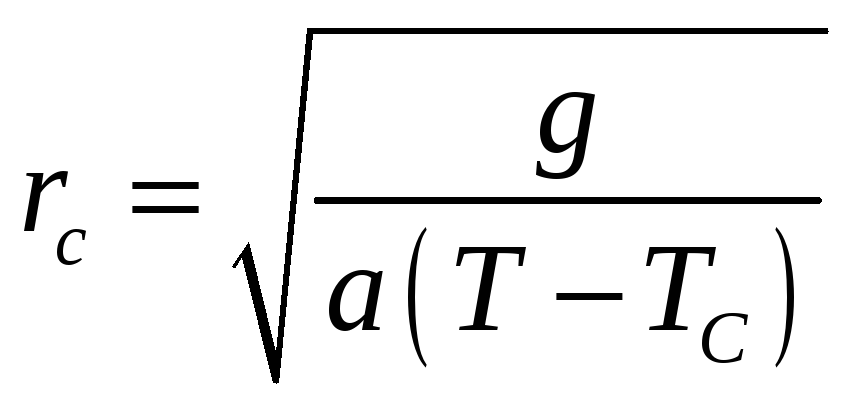. (10)

Величина называется корреляционным радиусом флуктуаций. Эта величина в соответствии в (9) определяет порядок величины расстояний, на которых корреляция существенно убывает. Видно, что корреляционный радиус возрастает при приближении к критической точке. В самой критической точке корреляционная функция имеет вид

Условие применимости теории флуктуаций состоит в том, чтобы флуктуация намагниченности была бы мала по сравнению с самой намагниченностью. Это означает неравенство

.

Подставляя в это соотношение выражения (2), (9) и (10), получим

(11)

Это означает, что нельзя слишком близко приближаться к критической точке. С другой стороны, должно быть