стат / Задача 8

Задача 8. Найти флуктуации величин

Решение. Рассмотрим замкнутую статистическую систему. Пусть в ней находится малая статистическая подсистема. В равновесии полную энтропию всей системы обозначим S₀. Она является функцией полной энергии всей системы. При малом отклонении подсистемы от равновесия (флуктуации) полная энтропия меняется на малую величину . При этом процессе идет обмен энергией между малой подсистемой и термостатом (оставшаяся часть всей системы). Таким образом,

Здесь величина относится к малой подсистеме. По определению , где - появившееся при флуктуации число состояний, w – вероятность указанной флуктуации, А – коэффициент пропорциональности. Итак,

.

Здесь мы опустили индекс 0, так как ввиду малости флуктуации значения температуры и давления для подсистемы и термостата совпадают друг с другом.

Рассматривая малое изменение энергии подсистемы как функцию ее энтропии и объема, разложим это изменение в ряд Тейлора

.

Первые два слагаемых являются знакопеременными при флуктуациях, и их можно опустить при усреднении по флуктуациям. Следовательно,

Перепишем это выражение в виде

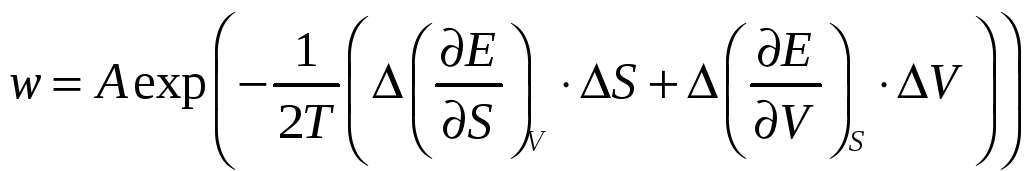
Так как

то окончательно получим общую формулу для вероятности флуктуации

. (1)

Выберем в качестве независимых переменных V, T. Тогда

так как

. (2)

Далее, аналогично

.

Подставляя эти соотношения в (1), находим

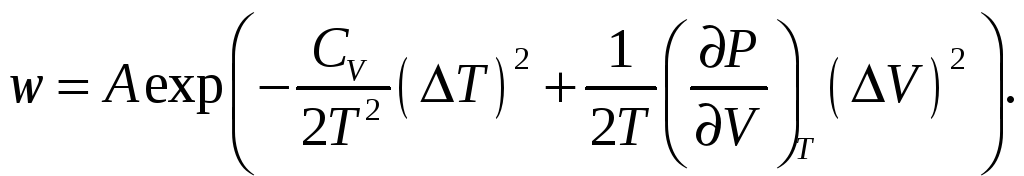
Так как произведение флуктуаций объема и температуры выпало из этого соотношения, то это означает, что указанные флуктуации являются независимыми друг от друга, т.е.

Каждая из флуктуаций описывается формулой Гаусса

(3)

Следовательно, находим:

(4)

Выберем теперь в качестве независимых переменных в (1) давление и энтропию. Тогда

Далее,

.

Так как дифференциал энтальпии равен , то

Следовательно,

.

Подставляя эти соотношения в (1), находим

Видно, что флуктуации давления и энтропии являются независимыми друг от друга. В соответствии с распределением Гаусса (3) отсюда находим

(5)

Далее найдем флуктуацию энергии. Имеем в переменных V,T (используя (2)):

.

Возводя в квадрат и усредняя, используем найденные выше для флуктуаций объема и температуры выражения (4)

(6)

Далее, найдем флуктуацию Имеем в переменных V,T

На основе (4) получим

(7)

Далее, найдем флуктуацию На основе (4) имеем

(8)

Найдем теперь флуктуацию Имеем в переменных V,T

.

На основе (4) имеем

(9)

Наконец, найдем флуктуацию Имеем в переменных V,T

Следовательно,

Подставляя (4) и учитывая (2), находим

(10)